12.4 河內塔問題¶

在合併排序和構建二元樹中，我們都是將原問題分解為兩個規模為原問題一半的子問題。然而對於河內塔問題，我們採用不同的分解策略。

Question

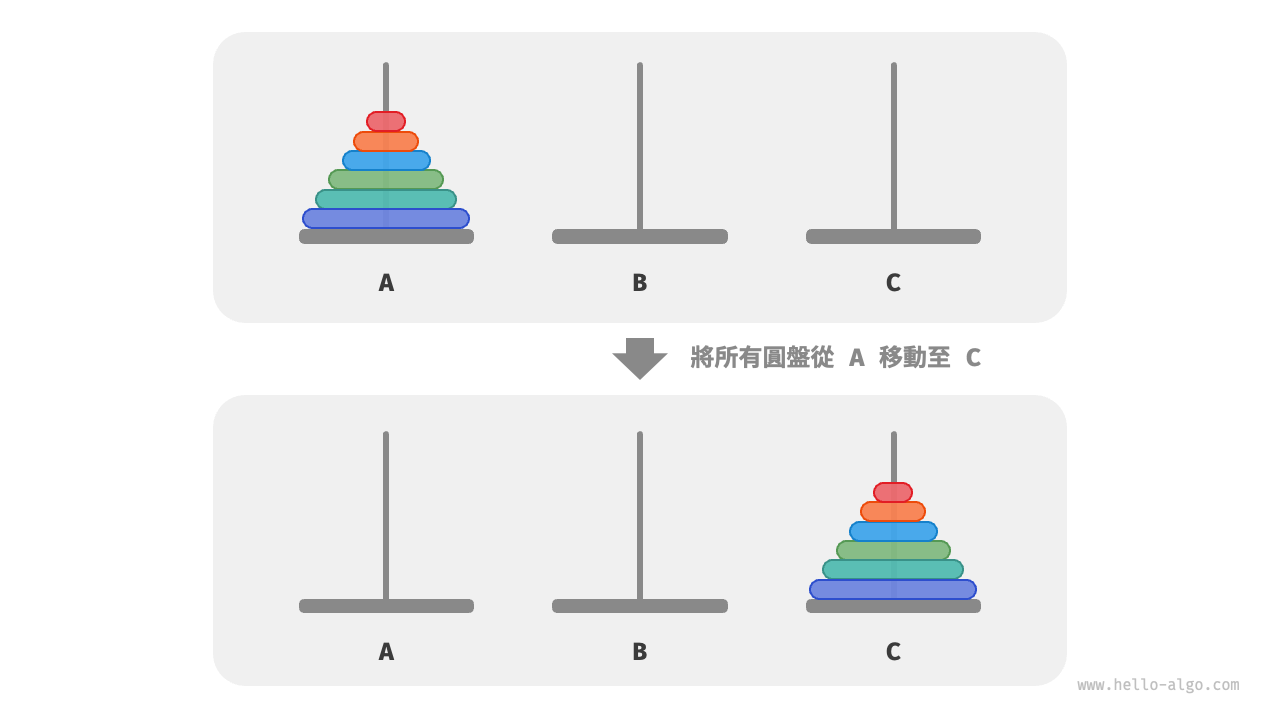
給定三根柱子，記為 A、B 和 C 。起始狀態下，柱子 A 上套著 \(n\) 個圓盤，它們從上到下按照從小到大的順序排列。我們的任務是要把這 \(n\) 個圓盤移到柱子 C 上，並保持它們的原有順序不變（如圖 12-10 所示）。在移動圓盤的過程中，需要遵守以下規則。

圓盤只能從一根柱子頂部拿出，從另一根柱子頂部放入。
每次只能移動一個圓盤。
小圓盤必須時刻位於大圓盤之上。

圖 12-10 河內塔問題示例

我們將規模為 \(i\) 的河內塔問題記作 \(f(i)\) 。例如 \(f(3)\) 代表將 \(3\) 個圓盤從 A 移動至 C 的河內塔問題。

1. 考慮基本情況¶

如圖 12-11 所示，對於問題 \(f(1)\) ，即當只有一個圓盤時，我們將它直接從 A 移動至 C 即可。

<1><2>

圖 12-11 規模為 1 的問題的解

如圖 12-12 所示，對於問題 \(f(2)\) ，即當有兩個圓盤時，由於要時刻滿足小圓盤在大圓盤之上，因此需要藉助 B 來完成移動。

先將上面的小圓盤從 A 移至 B 。
再將大圓盤從 A 移至 C 。
最後將小圓盤從 B 移至 C 。

<1><2><3><4>

圖 12-12 規模為 2 的問題的解

解決問題 \(f(2)\) 的過程可總結為：將兩個圓盤藉助 B 從 A 移至 C 。其中，C 稱為目標柱、B 稱為緩衝柱。

2. 子問題分解¶

對於問題 \(f(3)\) ，即當有三個圓盤時，情況變得稍微複雜了一些。

因為已知 \(f(1)\) 和 \(f(2)\) 的解，所以我們可從分治角度思考，將 A 頂部的兩個圓盤看作一個整體，執行圖 12-13 所示的步驟。這樣三個圓盤就被順利地從 A 移至 C 了。

令 B 為目標柱、C 為緩衝柱，將兩個圓盤從 A 移至 B 。
將 A 中剩餘的一個圓盤從 A 直接移動至 C 。
令 C 為目標柱、A 為緩衝柱，將兩個圓盤從 B 移至 C 。

<1><2><3><4>

圖 12-13 規模為 3 的問題的解

從本質上看，我們將問題 \(f(3)\) 劃分為兩個子問題 \(f(2)\) 和一個子問題 \(f(1)\) 。按順序解決這三個子問題之後，原問題隨之得到解決。這說明子問題是獨立的，而且解可以合併。

至此，我們可總結出圖 12-14 所示的解決河內塔問題的分治策略：將原問題 \(f(n)\) 劃分為兩個子問題 \(f(n-1)\) 和一個子問題 \(f(1)\) ，並按照以下順序解決這三個子問題。

將 \(n-1\) 個圓盤藉助 C 從 A 移至 B 。
將剩餘 \(1\) 個圓盤從 A 直接移至 C 。
將 \(n-1\) 個圓盤藉助 A 從 B 移至 C 。

對於這兩個子問題 \(f(n-1)\) ，可以透過相同的方式進行遞迴劃分，直至達到最小子問題 \(f(1)\) 。而 \(f(1)\) 的解是已知的，只需一次移動操作即可。

圖 12-14 解決河內塔問題的分治策略

3. 程式碼實現¶

在程式碼中，我們宣告一個遞迴函式 dfs(i, src, buf, tar) ，它的作用是將柱 src 頂部的 \(i\) 個圓盤藉助緩衝柱 buf 移動至目標柱 tar ：

PythonC++JavaC#GoSwiftJSTSDartRustCKotlinRubyZig

hanota.py

def move(src: list[int], tar: list[int]):
    """移動一個圓盤"""
    # 從 src 頂部拿出一個圓盤
    pan = src.pop()
    # 將圓盤放入 tar 頂部
    tar.append(pan)

def dfs(i: int, src: list[int], buf: list[int], tar: list[int]):
    """求解河內塔問題 f(i)"""
    # 若 src 只剩下一個圓盤，則直接將其移到 tar
    if i == 1:
        move(src, tar)
        return
    # 子問題 f(i-1) ：將 src 頂部 i-1 個圓盤藉助 tar 移到 buf
    dfs(i - 1, src, tar, buf)
    # 子問題 f(1) ：將 src 剩餘一個圓盤移到 tar
    move(src, tar)
    # 子問題 f(i-1) ：將 buf 頂部 i-1 個圓盤藉助 src 移到 tar
    dfs(i - 1, buf, src, tar)

def solve_hanota(A: list[int], B: list[int], C: list[int]):
    """求解河內塔問題"""
    n = len(A)
    # 將 A 頂部 n 個圓盤藉助 B 移到 C
    dfs(n, A, B, C)

hanota.cpp

/* 移動一個圓盤 */
void move(vector<int> &src, vector<int> &tar) {
    // 從 src 頂部拿出一個圓盤
    int pan = src.back();
    src.pop_back();
    // 將圓盤放入 tar 頂部
    tar.push_back(pan);
}

/* 求解河內塔問題 f(i) */
void dfs(int i, vector<int> &src, vector<int> &buf, vector<int> &tar) {
    // 若 src 只剩下一個圓盤，則直接將其移到 tar
    if (i == 1) {
        move(src, tar);
        return;
    }
    // 子問題 f(i-1) ：將 src 頂部 i-1 個圓盤藉助 tar 移到 buf
    dfs(i - 1, src, tar, buf);
    // 子問題 f(1) ：將 src 剩餘一個圓盤移到 tar
    move(src, tar);
    // 子問題 f(i-1) ：將 buf 頂部 i-1 個圓盤藉助 src 移到 tar
    dfs(i - 1, buf, src, tar);
}

/* 求解河內塔問題 */
void solveHanota(vector<int> &A, vector<int> &B, vector<int> &C) {
    int n = A.size();
    // 將 A 頂部 n 個圓盤藉助 B 移到 C
    dfs(n, A, B, C);
}

hanota.java

/* 移動一個圓盤 */
void move(List<Integer> src, List<Integer> tar) {
    // 從 src 頂部拿出一個圓盤
    Integer pan = src.remove(src.size() - 1);
    // 將圓盤放入 tar 頂部
    tar.add(pan);
}

/* 求解河內塔問題 f(i) */
void dfs(int i, List<Integer> src, List<Integer> buf, List<Integer> tar) {
    // 若 src 只剩下一個圓盤，則直接將其移到 tar
    if (i == 1) {
        move(src, tar);
        return;
    }
    // 子問題 f(i-1) ：將 src 頂部 i-1 個圓盤藉助 tar 移到 buf
    dfs(i - 1, src, tar, buf);
    // 子問題 f(1) ：將 src 剩餘一個圓盤移到 tar
    move(src, tar);
    // 子問題 f(i-1) ：將 buf 頂部 i-1 個圓盤藉助 src 移到 tar
    dfs(i - 1, buf, src, tar);
}

/* 求解河內塔問題 */
void solveHanota(List<Integer> A, List<Integer> B, List<Integer> C) {
    int n = A.size();
    // 將 A 頂部 n 個圓盤藉助 B 移到 C
    dfs(n, A, B, C);
}

hanota.cs

/* 移動一個圓盤 */
void Move(List<int> src, List<int> tar) {
    // 從 src 頂部拿出一個圓盤
    int pan = src[^1];
    src.RemoveAt(src.Count - 1);
    // 將圓盤放入 tar 頂部
    tar.Add(pan);
}

/* 求解河內塔問題 f(i) */
void DFS(int i, List<int> src, List<int> buf, List<int> tar) {
    // 若 src 只剩下一個圓盤，則直接將其移到 tar
    if (i == 1) {
        Move(src, tar);
        return;
    }
    // 子問題 f(i-1) ：將 src 頂部 i-1 個圓盤藉助 tar 移到 buf
    DFS(i - 1, src, tar, buf);
    // 子問題 f(1) ：將 src 剩餘一個圓盤移到 tar
    Move(src, tar);
    // 子問題 f(i-1) ：將 buf 頂部 i-1 個圓盤藉助 src 移到 tar
    DFS(i - 1, buf, src, tar);
}

/* 求解河內塔問題 */
void SolveHanota(List<int> A, List<int> B, List<int> C) {
    int n = A.Count;
    // 將 A 頂部 n 個圓盤藉助 B 移到 C
    DFS(n, A, B, C);
}

hanota.go

/* 移動一個圓盤 */
func move(src, tar *list.List) {
    // 從 src 頂部拿出一個圓盤
    pan := src.Back()
    // 將圓盤放入 tar 頂部
    tar.PushBack(pan.Value)
    // 移除 src 頂部圓盤
    src.Remove(pan)
}

/* 求解河內塔問題 f(i) */
func dfsHanota(i int, src, buf, tar *list.List) {
    // 若 src 只剩下一個圓盤，則直接將其移到 tar
    if i == 1 {
        move(src, tar)
        return
    }
    // 子問題 f(i-1) ：將 src 頂部 i-1 個圓盤藉助 tar 移到 buf
    dfsHanota(i-1, src, tar, buf)
    // 子問題 f(1) ：將 src 剩餘一個圓盤移到 tar
    move(src, tar)
    // 子問題 f(i-1) ：將 buf 頂部 i-1 個圓盤藉助 src 移到 tar
    dfsHanota(i-1, buf, src, tar)
}

/* 求解河內塔問題 */
func solveHanota(A, B, C *list.List) {
    n := A.Len()
    // 將 A 頂部 n 個圓盤藉助 B 移到 C
    dfsHanota(n, A, B, C)
}

hanota.swift

/* 移動一個圓盤 */
func move(src: inout [Int], tar: inout [Int]) {
    // 從 src 頂部拿出一個圓盤
    let pan = src.popLast()!
    // 將圓盤放入 tar 頂部
    tar.append(pan)
}

/* 求解河內塔問題 f(i) */
func dfs(i: Int, src: inout [Int], buf: inout [Int], tar: inout [Int]) {
    // 若 src 只剩下一個圓盤，則直接將其移到 tar
    if i == 1 {
        move(src: &src, tar: &tar)
        return
    }
    // 子問題 f(i-1) ：將 src 頂部 i-1 個圓盤藉助 tar 移到 buf
    dfs(i: i - 1, src: &src, buf: &tar, tar: &buf)
    // 子問題 f(1) ：將 src 剩餘一個圓盤移到 tar
    move(src: &src, tar: &tar)
    // 子問題 f(i-1) ：將 buf 頂部 i-1 個圓盤藉助 src 移到 tar
    dfs(i: i - 1, src: &buf, buf: &src, tar: &tar)
}

/* 求解河內塔問題 */
func solveHanota(A: inout [Int], B: inout [Int], C: inout [Int]) {
    let n = A.count
    // 串列尾部是柱子頂部
    // 將 src 頂部 n 個圓盤藉助 B 移到 C
    dfs(i: n, src: &A, buf: &B, tar: &C)
}

hanota.js

/* 移動一個圓盤 */
function move(src, tar) {
    // 從 src 頂部拿出一個圓盤
    const pan = src.pop();
    // 將圓盤放入 tar 頂部
    tar.push(pan);
}

/* 求解河內塔問題 f(i) */
function dfs(i, src, buf, tar) {
    // 若 src 只剩下一個圓盤，則直接將其移到 tar
    if (i === 1) {
        move(src, tar);
        return;
    }
    // 子問題 f(i-1) ：將 src 頂部 i-1 個圓盤藉助 tar 移到 buf
    dfs(i - 1, src, tar, buf);
    // 子問題 f(1) ：將 src 剩餘一個圓盤移到 tar
    move(src, tar);
    // 子問題 f(i-1) ：將 buf 頂部 i-1 個圓盤藉助 src 移到 tar
    dfs(i - 1, buf, src, tar);
}

/* 求解河內塔問題 */
function solveHanota(A, B, C) {
    const n = A.length;
    // 將 A 頂部 n 個圓盤藉助 B 移到 C
    dfs(n, A, B, C);
}

hanota.ts

/* 移動一個圓盤 */
function move(src: number[], tar: number[]): void {
    // 從 src 頂部拿出一個圓盤
    const pan = src.pop();
    // 將圓盤放入 tar 頂部
    tar.push(pan);
}

/* 求解河內塔問題 f(i) */
function dfs(i: number, src: number[], buf: number[], tar: number[]): void {
    // 若 src 只剩下一個圓盤，則直接將其移到 tar
    if (i === 1) {
        move(src, tar);
        return;
    }
    // 子問題 f(i-1) ：將 src 頂部 i-1 個圓盤藉助 tar 移到 buf
    dfs(i - 1, src, tar, buf);
    // 子問題 f(1) ：將 src 剩餘一個圓盤移到 tar
    move(src, tar);
    // 子問題 f(i-1) ：將 buf 頂部 i-1 個圓盤藉助 src 移到 tar
    dfs(i - 1, buf, src, tar);
}

/* 求解河內塔問題 */
function solveHanota(A: number[], B: number[], C: number[]): void {
    const n = A.length;
    // 將 A 頂部 n 個圓盤藉助 B 移到 C
    dfs(n, A, B, C);
}

hanota.dart

/* 移動一個圓盤 */
void move(List<int> src, List<int> tar) {
  // 從 src 頂部拿出一個圓盤
  int pan = src.removeLast();
  // 將圓盤放入 tar 頂部
  tar.add(pan);
}

/* 求解河內塔問題 f(i) */
void dfs(int i, List<int> src, List<int> buf, List<int> tar) {
  // 若 src 只剩下一個圓盤，則直接將其移到 tar
  if (i == 1) {
    move(src, tar);
    return;
  }
  // 子問題 f(i-1) ：將 src 頂部 i-1 個圓盤藉助 tar 移到 buf
  dfs(i - 1, src, tar, buf);
  // 子問題 f(1) ：將 src 剩餘一個圓盤移到 tar
  move(src, tar);
  // 子問題 f(i-1) ：將 buf 頂部 i-1 個圓盤藉助 src 移到 tar
  dfs(i - 1, buf, src, tar);
}

/* 求解河內塔問題 */
void solveHanota(List<int> A, List<int> B, List<int> C) {
  int n = A.length;
  // 將 A 頂部 n 個圓盤藉助 B 移到 C
  dfs(n, A, B, C);
}

hanota.rs

/* 移動一個圓盤 */
fn move_pan(src: &mut Vec<i32>, tar: &mut Vec<i32>) {
    // 從 src 頂部拿出一個圓盤
    let pan = src.remove(src.len() - 1);
    // 將圓盤放入 tar 頂部
    tar.push(pan);
}

/* 求解河內塔問題 f(i) */
fn dfs(i: i32, src: &mut Vec<i32>, buf: &mut Vec<i32>, tar: &mut Vec<i32>) {
    // 若 src 只剩下一個圓盤，則直接將其移到 tar
    if i == 1 {
        move_pan(src, tar);
        return;
    }
    // 子問題 f(i-1) ：將 src 頂部 i-1 個圓盤藉助 tar 移到 buf
    dfs(i - 1, src, tar, buf);
    // 子問題 f(1) ：將 src 剩餘一個圓盤移到 tar
    move_pan(src, tar);
    // 子問題 f(i-1) ：將 buf 頂部 i-1 個圓盤藉助 src 移到 tar
    dfs(i - 1, buf, src, tar);
}

/* 求解河內塔問題 */
fn solve_hanota(A: &mut Vec<i32>, B: &mut Vec<i32>, C: &mut Vec<i32>) {
    let n = A.len() as i32;
    // 將 A 頂部 n 個圓盤藉助 B 移到 C
    dfs(n, A, B, C);
}

hanota.c

/* 移動一個圓盤 */
void move(int *src, int *srcSize, int *tar, int *tarSize) {
    // 從 src 頂部拿出一個圓盤
    int pan = src[*srcSize - 1];
    src[*srcSize - 1] = 0;
    (*srcSize)--;
    // 將圓盤放入 tar 頂部
    tar[*tarSize] = pan;
    (*tarSize)++;
}

/* 求解河內塔問題 f(i) */
void dfs(int i, int *src, int *srcSize, int *buf, int *bufSize, int *tar, int *tarSize) {
    // 若 src 只剩下一個圓盤，則直接將其移到 tar
    if (i == 1) {
        move(src, srcSize, tar, tarSize);
        return;
    }
    // 子問題 f(i-1) ：將 src 頂部 i-1 個圓盤藉助 tar 移到 buf
    dfs(i - 1, src, srcSize, tar, tarSize, buf, bufSize);
    // 子問題 f(1) ：將 src 剩餘一個圓盤移到 tar
    move(src, srcSize, tar, tarSize);
    // 子問題 f(i-1) ：將 buf 頂部 i-1 個圓盤藉助 src 移到 tar
    dfs(i - 1, buf, bufSize, src, srcSize, tar, tarSize);
}

/* 求解河內塔問題 */
void solveHanota(int *A, int *ASize, int *B, int *BSize, int *C, int *CSize) {
    // 將 A 頂部 n 個圓盤藉助 B 移到 C
    dfs(*ASize, A, ASize, B, BSize, C, CSize);
}

hanota.kt

/* 移動一個圓盤 */
fun move(src: MutableList<Int>, tar: MutableList<Int>) {
    // 從 src 頂部拿出一個圓盤
    val pan: Int = src.removeAt(src.size - 1)
    // 將圓盤放入 tar 頂部
    tar.add(pan)
}

/* 求解河內塔問題 f(i) */
fun dfs(i: Int, src: MutableList<Int>, buf: MutableList<Int>, tar: MutableList<Int>) {
    // 若 src 只剩下一個圓盤，則直接將其移到 tar
    if (i == 1) {
        move(src, tar)
        return
    }
    // 子問題 f(i-1) ：將 src 頂部 i-1 個圓盤藉助 tar 移到 buf
    dfs(i - 1, src, tar, buf)
    // 子問題 f(1) ：將 src 剩餘一個圓盤移到 tar
    move(src, tar)
    // 子問題 f(i-1) ：將 buf 頂部 i-1 個圓盤藉助 src 移到 tar
    dfs(i - 1, buf, src, tar)
}

/* 求解河內塔問題 */
fun solveHanota(A: MutableList<Int>, B: MutableList<Int>, C: MutableList<Int>) {
    val n = A.size
    // 將 A 頂部 n 個圓盤藉助 B 移到 C
    dfs(n, A, B, C)
}

hanota.rb

[class]{}-[func]{move}

[class]{}-[func]{dfs}

[class]{}-[func]{solve_hanota}

hanota.zig

[class]{}-[func]{move}

[class]{}-[func]{dfs}

[class]{}-[func]{solveHanota}

視覺化執行

全螢幕觀看 >

如圖 12-15 所示，河內塔問題形成一棵高度為 \(n\) 的遞迴樹，每個節點代表一個子問題，對應一個開啟的 dfs() 函式，因此時間複雜度為 \(O(2^n)\) ，空間複雜度為 \(O(n)\) 。

圖 12-15 河內塔問題的遞迴樹

Quote

河內塔問題源自一個古老的傳說。在古印度的一個寺廟裡，僧侶們有三根高大的鑽石柱子，以及 \(64\) 個大小不一的金圓盤。僧侶們不斷地移動圓盤，他們相信在最後一個圓盤被正確放置的那一刻，這個世界就會結束。

然而，即使僧侶們每秒鐘移動一次，總共需要大約 \(2^{64} \approx 1.84×10^{19}\) 秒，合約 \(5850\) 億年，遠遠超過了現在對宇宙年齡的估計。所以，倘若這個傳說是真的，我們應該不需要擔心世界末日的到來。