7.2 二元樹走訪¶
從物理結構的角度來看,樹是一種基於鏈結串列的資料結構,因此其走訪方式是透過指標逐個訪問節點。然而,樹是一種非線性資料結構,這使得走訪樹比走訪鏈結串列更加複雜,需要藉助搜尋演算法來實現。
二元樹常見的走訪方式包括層序走訪、前序走訪、中序走訪和後序走訪等。
7.2.1 層序走訪¶
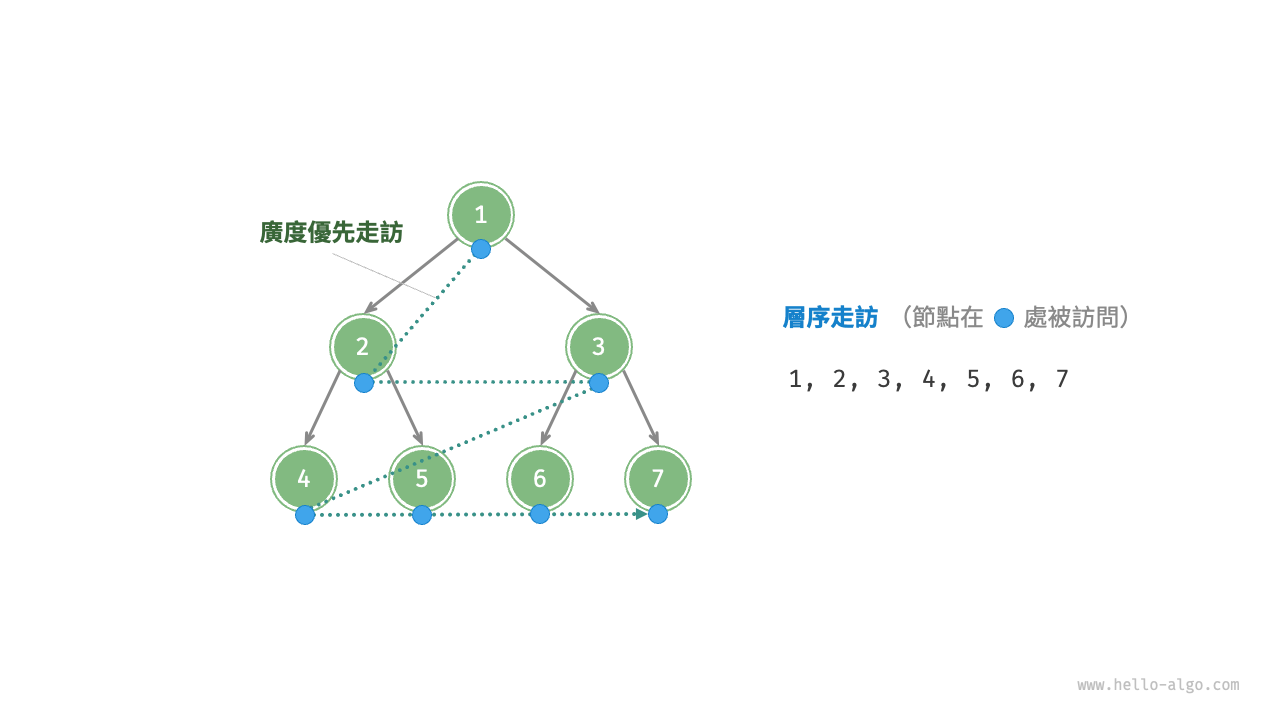
如圖 7-9 所示,層序走訪(level-order traversal)從頂部到底部逐層走訪二元樹,並在每一層按照從左到右的順序訪問節點。
層序走訪本質上屬於廣度優先走訪(breadth-first traversal),也稱廣度優先搜尋(breadth-first search, BFS),它體現了一種“一圈一圈向外擴展”的逐層走訪方式。
圖 7-9 二元樹的層序走訪
1. 程式碼實現¶
廣度優先走訪通常藉助“佇列”來實現。佇列遵循“先進先出”的規則,而廣度優先走訪則遵循“逐層推進”的規則,兩者背後的思想是一致的。實現程式碼如下:
binary_tree_bfs.py
def level_order(root: TreeNode | None) -> list[int]:
"""層序走訪"""
# 初始化佇列,加入根節點
queue: deque[TreeNode] = deque()
queue.append(root)
# 初始化一個串列,用於儲存走訪序列
res = []
while queue:
node: TreeNode = queue.popleft() # 隊列出隊
res.append(node.val) # 儲存節點值
if node.left is not None:
queue.append(node.left) # 左子節點入列
if node.right is not None:
queue.append(node.right) # 右子節點入列
return res
binary_tree_bfs.cpp
/* 層序走訪 */
vector<int> levelOrder(TreeNode *root) {
// 初始化佇列,加入根節點
queue<TreeNode *> queue;
queue.push(root);
// 初始化一個串列,用於儲存走訪序列
vector<int> vec;
while (!queue.empty()) {
TreeNode *node = queue.front();
queue.pop(); // 隊列出隊
vec.push_back(node->val); // 儲存節點值
if (node->left != nullptr)
queue.push(node->left); // 左子節點入列
if (node->right != nullptr)
queue.push(node->right); // 右子節點入列
}
return vec;
}
binary_tree_bfs.java
/* 層序走訪 */
List<Integer> levelOrder(TreeNode root) {
// 初始化佇列,加入根節點
Queue<TreeNode> queue = new LinkedList<>();
queue.add(root);
// 初始化一個串列,用於儲存走訪序列
List<Integer> list = new ArrayList<>();
while (!queue.isEmpty()) {
TreeNode node = queue.poll(); // 隊列出隊
list.add(node.val); // 儲存節點值
if (node.left != null)
queue.offer(node.left); // 左子節點入列
if (node.right != null)
queue.offer(node.right); // 右子節點入列
}
return list;
}
binary_tree_bfs.cs
/* 層序走訪 */
List<int> LevelOrder(TreeNode root) {
// 初始化佇列,加入根節點
Queue<TreeNode> queue = new();
queue.Enqueue(root);
// 初始化一個串列,用於儲存走訪序列
List<int> list = [];
while (queue.Count != 0) {
TreeNode node = queue.Dequeue(); // 隊列出隊
list.Add(node.val!.Value); // 儲存節點值
if (node.left != null)
queue.Enqueue(node.left); // 左子節點入列
if (node.right != null)
queue.Enqueue(node.right); // 右子節點入列
}
return list;
}
binary_tree_bfs.go
/* 層序走訪 */
func levelOrder(root *TreeNode) []any {
// 初始化佇列,加入根節點
queue := list.New()
queue.PushBack(root)
// 初始化一個切片,用於儲存走訪序列
nums := make([]any, 0)
for queue.Len() > 0 {
// 隊列出隊
node := queue.Remove(queue.Front()).(*TreeNode)
// 儲存節點值
nums = append(nums, node.Val)
if node.Left != nil {
// 左子節點入列
queue.PushBack(node.Left)
}
if node.Right != nil {
// 右子節點入列
queue.PushBack(node.Right)
}
}
return nums
}
binary_tree_bfs.swift
/* 層序走訪 */
func levelOrder(root: TreeNode) -> [Int] {
// 初始化佇列,加入根節點
var queue: [TreeNode] = [root]
// 初始化一個串列,用於儲存走訪序列
var list: [Int] = []
while !queue.isEmpty {
let node = queue.removeFirst() // 隊列出隊
list.append(node.val) // 儲存節點值
if let left = node.left {
queue.append(left) // 左子節點入列
}
if let right = node.right {
queue.append(right) // 右子節點入列
}
}
return list
}
binary_tree_bfs.js
/* 層序走訪 */
function levelOrder(root) {
// 初始化佇列,加入根節點
const queue = [root];
// 初始化一個串列,用於儲存走訪序列
const list = [];
while (queue.length) {
let node = queue.shift(); // 隊列出隊
list.push(node.val); // 儲存節點值
if (node.left) queue.push(node.left); // 左子節點入列
if (node.right) queue.push(node.right); // 右子節點入列
}
return list;
}
binary_tree_bfs.ts
/* 層序走訪 */
function levelOrder(root: TreeNode | null): number[] {
// 初始化佇列,加入根節點
const queue = [root];
// 初始化一個串列,用於儲存走訪序列
const list: number[] = [];
while (queue.length) {
let node = queue.shift() as TreeNode; // 隊列出隊
list.push(node.val); // 儲存節點值
if (node.left) {
queue.push(node.left); // 左子節點入列
}
if (node.right) {
queue.push(node.right); // 右子節點入列
}
}
return list;
}
binary_tree_bfs.dart
/* 層序走訪 */
List<int> levelOrder(TreeNode? root) {
// 初始化佇列,加入根節點
Queue<TreeNode?> queue = Queue();
queue.add(root);
// 初始化一個串列,用於儲存走訪序列
List<int> res = [];
while (queue.isNotEmpty) {
TreeNode? node = queue.removeFirst(); // 隊列出隊
res.add(node!.val); // 儲存節點值
if (node.left != null) queue.add(node.left); // 左子節點入列
if (node.right != null) queue.add(node.right); // 右子節點入列
}
return res;
}
binary_tree_bfs.rs
/* 層序走訪 */
fn level_order(root: &Rc<RefCell<TreeNode>>) -> Vec<i32> {
// 初始化佇列,加入根節點
let mut que = VecDeque::new();
que.push_back(Rc::clone(&root));
// 初始化一個串列,用於儲存走訪序列
let mut vec = Vec::new();
while let Some(node) = que.pop_front() {
// 隊列出隊
vec.push(node.borrow().val); // 儲存節點值
if let Some(left) = node.borrow().left.as_ref() {
que.push_back(Rc::clone(left)); // 左子節點入列
}
if let Some(right) = node.borrow().right.as_ref() {
que.push_back(Rc::clone(right)); // 右子節點入列
};
}
vec
}
binary_tree_bfs.c
/* 層序走訪 */
int *levelOrder(TreeNode *root, int *size) {
/* 輔助佇列 */
int front, rear;
int index, *arr;
TreeNode *node;
TreeNode **queue;
/* 輔助佇列 */
queue = (TreeNode **)malloc(sizeof(TreeNode *) * MAX_SIZE);
// 佇列指標
front = 0, rear = 0;
// 加入根節點
queue[rear++] = root;
// 初始化一個串列,用於儲存走訪序列
/* 輔助陣列 */
arr = (int *)malloc(sizeof(int) * MAX_SIZE);
// 陣列指標
index = 0;
while (front < rear) {
// 隊列出隊
node = queue[front++];
// 儲存節點值
arr[index++] = node->val;
if (node->left != NULL) {
// 左子節點入列
queue[rear++] = node->left;
}
if (node->right != NULL) {
// 右子節點入列
queue[rear++] = node->right;
}
}
// 更新陣列長度的值
*size = index;
arr = realloc(arr, sizeof(int) * (*size));
// 釋放輔助陣列空間
free(queue);
return arr;
}
binary_tree_bfs.kt
/* 層序走訪 */
fun levelOrder(root: TreeNode?): MutableList<Int> {
// 初始化佇列,加入根節點
val queue = LinkedList<TreeNode?>()
queue.add(root)
// 初始化一個串列,用於儲存走訪序列
val list = ArrayList<Int>()
while (!queue.isEmpty()) {
val node = queue.poll() // 隊列出隊
list.add(node?.value!!) // 儲存節點值
if (node.left != null) queue.offer(node.left) // 左子節點入列
if (node.right != null) queue.offer(node.right) // 右子節點入列
}
return list
}
binary_tree_bfs.zig
// 層序走訪
fn levelOrder(comptime T: type, mem_allocator: std.mem.Allocator, root: *inc.TreeNode(T)) !std.ArrayList(T) {
// 初始化佇列,加入根節點
const L = std.TailQueue(*inc.TreeNode(T));
var queue = L{};
var root_node = try mem_allocator.create(L.Node);
root_node.data = root;
queue.append(root_node);
// 初始化一個串列,用於儲存走訪序列
var list = std.ArrayList(T).init(std.heap.page_allocator);
while (queue.len > 0) {
var queue_node = queue.popFirst().?; // 隊列出隊
var node = queue_node.data;
try list.append(node.val); // 儲存節點值
if (node.left != null) {
var tmp_node = try mem_allocator.create(L.Node);
tmp_node.data = node.left.?;
queue.append(tmp_node); // 左子節點入列
}
if (node.right != null) {
var tmp_node = try mem_allocator.create(L.Node);
tmp_node.data = node.right.?;
queue.append(tmp_node); // 右子節點入列
}
}
return list;
}
視覺化執行
2. 複雜度分析¶
- 時間複雜度為 \(O(n)\) :所有節點被訪問一次,使用 \(O(n)\) 時間,其中 \(n\) 為節點數量。
- 空間複雜度為 \(O(n)\) :在最差情況下,即滿二元樹時,走訪到最底層之前,佇列中最多同時存在 \((n + 1) / 2\) 個節點,佔用 \(O(n)\) 空間。
7.2.2 前序、中序、後序走訪¶
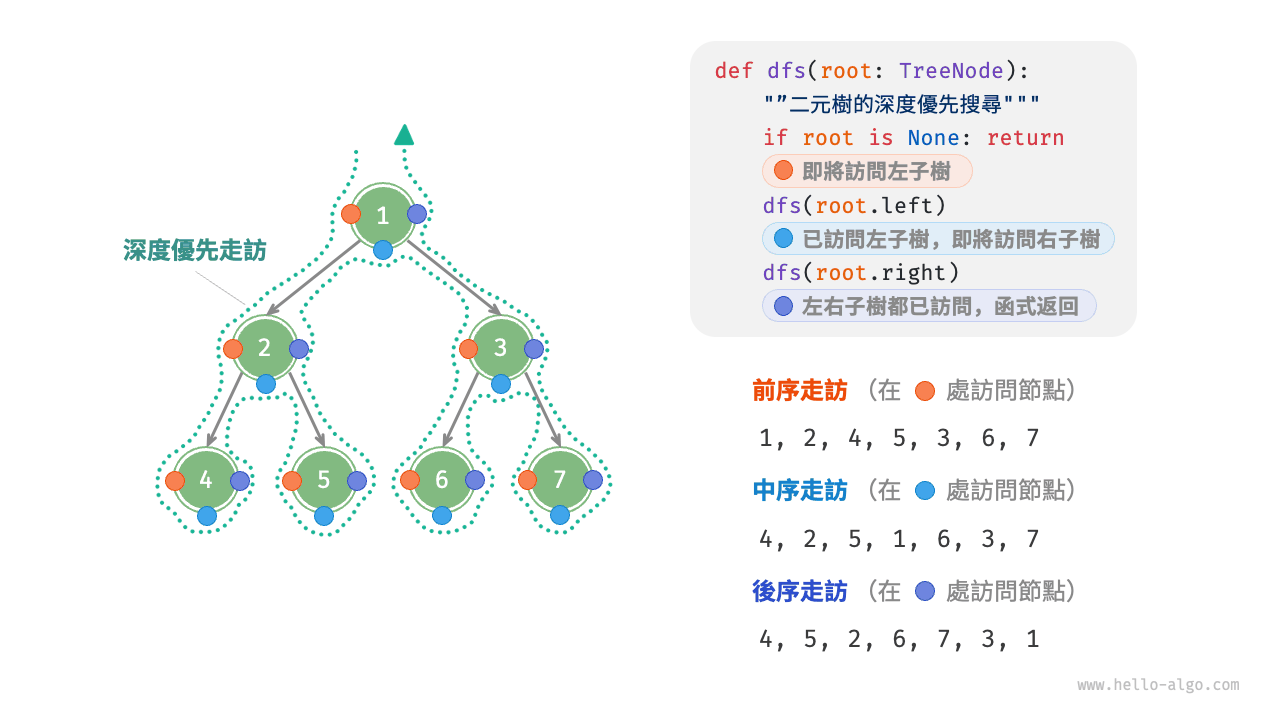
相應地,前序、中序和後序走訪都屬於深度優先走訪(depth-first traversal),也稱深度優先搜尋(depth-first search, DFS),它體現了一種“先走到盡頭,再回溯繼續”的走訪方式。
圖 7-10 展示了對二元樹進行深度優先走訪的工作原理。深度優先走訪就像是繞著整棵二元樹的外圍“走”一圈,在每個節點都會遇到三個位置,分別對應前序走訪、中序走訪和後序走訪。
圖 7-10 二元搜尋樹的前序、中序、後序走訪
1. 程式碼實現¶
深度優先搜尋通常基於遞迴實現:
binary_tree_dfs.py
def pre_order(root: TreeNode | None):
"""前序走訪"""
if root is None:
return
# 訪問優先順序:根節點 -> 左子樹 -> 右子樹
res.append(root.val)
pre_order(root=root.left)
pre_order(root=root.right)
def in_order(root: TreeNode | None):
"""中序走訪"""
if root is None:
return
# 訪問優先順序:左子樹 -> 根節點 -> 右子樹
in_order(root=root.left)
res.append(root.val)
in_order(root=root.right)
def post_order(root: TreeNode | None):
"""後序走訪"""
if root is None:
return
# 訪問優先順序:左子樹 -> 右子樹 -> 根節點
post_order(root=root.left)
post_order(root=root.right)
res.append(root.val)
binary_tree_dfs.cpp
/* 前序走訪 */
void preOrder(TreeNode *root) {
if (root == nullptr)
return;
// 訪問優先順序:根節點 -> 左子樹 -> 右子樹
vec.push_back(root->val);
preOrder(root->left);
preOrder(root->right);
}
/* 中序走訪 */
void inOrder(TreeNode *root) {
if (root == nullptr)
return;
// 訪問優先順序:左子樹 -> 根節點 -> 右子樹
inOrder(root->left);
vec.push_back(root->val);
inOrder(root->right);
}
/* 後序走訪 */
void postOrder(TreeNode *root) {
if (root == nullptr)
return;
// 訪問優先順序:左子樹 -> 右子樹 -> 根節點
postOrder(root->left);
postOrder(root->right);
vec.push_back(root->val);
}
binary_tree_dfs.java
/* 前序走訪 */
void preOrder(TreeNode root) {
if (root == null)
return;
// 訪問優先順序:根節點 -> 左子樹 -> 右子樹
list.add(root.val);
preOrder(root.left);
preOrder(root.right);
}
/* 中序走訪 */
void inOrder(TreeNode root) {
if (root == null)
return;
// 訪問優先順序:左子樹 -> 根節點 -> 右子樹
inOrder(root.left);
list.add(root.val);
inOrder(root.right);
}
/* 後序走訪 */
void postOrder(TreeNode root) {
if (root == null)
return;
// 訪問優先順序:左子樹 -> 右子樹 -> 根節點
postOrder(root.left);
postOrder(root.right);
list.add(root.val);
}
binary_tree_dfs.cs
/* 前序走訪 */
void PreOrder(TreeNode? root) {
if (root == null) return;
// 訪問優先順序:根節點 -> 左子樹 -> 右子樹
list.Add(root.val!.Value);
PreOrder(root.left);
PreOrder(root.right);
}
/* 中序走訪 */
void InOrder(TreeNode? root) {
if (root == null) return;
// 訪問優先順序:左子樹 -> 根節點 -> 右子樹
InOrder(root.left);
list.Add(root.val!.Value);
InOrder(root.right);
}
/* 後序走訪 */
void PostOrder(TreeNode? root) {
if (root == null) return;
// 訪問優先順序:左子樹 -> 右子樹 -> 根節點
PostOrder(root.left);
PostOrder(root.right);
list.Add(root.val!.Value);
}
binary_tree_dfs.go
/* 前序走訪 */
func preOrder(node *TreeNode) {
if node == nil {
return
}
// 訪問優先順序:根節點 -> 左子樹 -> 右子樹
nums = append(nums, node.Val)
preOrder(node.Left)
preOrder(node.Right)
}
/* 中序走訪 */
func inOrder(node *TreeNode) {
if node == nil {
return
}
// 訪問優先順序:左子樹 -> 根節點 -> 右子樹
inOrder(node.Left)
nums = append(nums, node.Val)
inOrder(node.Right)
}
/* 後序走訪 */
func postOrder(node *TreeNode) {
if node == nil {
return
}
// 訪問優先順序:左子樹 -> 右子樹 -> 根節點
postOrder(node.Left)
postOrder(node.Right)
nums = append(nums, node.Val)
}
binary_tree_dfs.swift
/* 前序走訪 */
func preOrder(root: TreeNode?) {
guard let root = root else {
return
}
// 訪問優先順序:根節點 -> 左子樹 -> 右子樹
list.append(root.val)
preOrder(root: root.left)
preOrder(root: root.right)
}
/* 中序走訪 */
func inOrder(root: TreeNode?) {
guard let root = root else {
return
}
// 訪問優先順序:左子樹 -> 根節點 -> 右子樹
inOrder(root: root.left)
list.append(root.val)
inOrder(root: root.right)
}
/* 後序走訪 */
func postOrder(root: TreeNode?) {
guard let root = root else {
return
}
// 訪問優先順序:左子樹 -> 右子樹 -> 根節點
postOrder(root: root.left)
postOrder(root: root.right)
list.append(root.val)
}
binary_tree_dfs.js
/* 前序走訪 */
function preOrder(root) {
if (root === null) return;
// 訪問優先順序:根節點 -> 左子樹 -> 右子樹
list.push(root.val);
preOrder(root.left);
preOrder(root.right);
}
/* 中序走訪 */
function inOrder(root) {
if (root === null) return;
// 訪問優先順序:左子樹 -> 根節點 -> 右子樹
inOrder(root.left);
list.push(root.val);
inOrder(root.right);
}
/* 後序走訪 */
function postOrder(root) {
if (root === null) return;
// 訪問優先順序:左子樹 -> 右子樹 -> 根節點
postOrder(root.left);
postOrder(root.right);
list.push(root.val);
}
binary_tree_dfs.ts
/* 前序走訪 */
function preOrder(root: TreeNode | null): void {
if (root === null) {
return;
}
// 訪問優先順序:根節點 -> 左子樹 -> 右子樹
list.push(root.val);
preOrder(root.left);
preOrder(root.right);
}
/* 中序走訪 */
function inOrder(root: TreeNode | null): void {
if (root === null) {
return;
}
// 訪問優先順序:左子樹 -> 根節點 -> 右子樹
inOrder(root.left);
list.push(root.val);
inOrder(root.right);
}
/* 後序走訪 */
function postOrder(root: TreeNode | null): void {
if (root === null) {
return;
}
// 訪問優先順序:左子樹 -> 右子樹 -> 根節點
postOrder(root.left);
postOrder(root.right);
list.push(root.val);
}
binary_tree_dfs.dart
/* 前序走訪 */
void preOrder(TreeNode? node) {
if (node == null) return;
// 訪問優先順序:根節點 -> 左子樹 -> 右子樹
list.add(node.val);
preOrder(node.left);
preOrder(node.right);
}
/* 中序走訪 */
void inOrder(TreeNode? node) {
if (node == null) return;
// 訪問優先順序:左子樹 -> 根節點 -> 右子樹
inOrder(node.left);
list.add(node.val);
inOrder(node.right);
}
/* 後序走訪 */
void postOrder(TreeNode? node) {
if (node == null) return;
// 訪問優先順序:左子樹 -> 右子樹 -> 根節點
postOrder(node.left);
postOrder(node.right);
list.add(node.val);
}
binary_tree_dfs.rs
/* 前序走訪 */
fn pre_order(root: Option<&Rc<RefCell<TreeNode>>>) -> Vec<i32> {
let mut result = vec![];
if let Some(node) = root {
// 訪問優先順序:根節點 -> 左子樹 -> 右子樹
result.push(node.borrow().val);
result.append(&mut pre_order(node.borrow().left.as_ref()));
result.append(&mut pre_order(node.borrow().right.as_ref()));
}
result
}
/* 中序走訪 */
fn in_order(root: Option<&Rc<RefCell<TreeNode>>>) -> Vec<i32> {
let mut result = vec![];
if let Some(node) = root {
// 訪問優先順序:左子樹 -> 根節點 -> 右子樹
result.append(&mut in_order(node.borrow().left.as_ref()));
result.push(node.borrow().val);
result.append(&mut in_order(node.borrow().right.as_ref()));
}
result
}
/* 後序走訪 */
fn post_order(root: Option<&Rc<RefCell<TreeNode>>>) -> Vec<i32> {
let mut result = vec![];
if let Some(node) = root {
// 訪問優先順序:左子樹 -> 右子樹 -> 根節點
result.append(&mut post_order(node.borrow().left.as_ref()));
result.append(&mut post_order(node.borrow().right.as_ref()));
result.push(node.borrow().val);
}
result
}
binary_tree_dfs.c
/* 前序走訪 */
void preOrder(TreeNode *root, int *size) {
if (root == NULL)
return;
// 訪問優先順序:根節點 -> 左子樹 -> 右子樹
arr[(*size)++] = root->val;
preOrder(root->left, size);
preOrder(root->right, size);
}
/* 中序走訪 */
void inOrder(TreeNode *root, int *size) {
if (root == NULL)
return;
// 訪問優先順序:左子樹 -> 根節點 -> 右子樹
inOrder(root->left, size);
arr[(*size)++] = root->val;
inOrder(root->right, size);
}
/* 後序走訪 */
void postOrder(TreeNode *root, int *size) {
if (root == NULL)
return;
// 訪問優先順序:左子樹 -> 右子樹 -> 根節點
postOrder(root->left, size);
postOrder(root->right, size);
arr[(*size)++] = root->val;
}
binary_tree_dfs.kt
/* 前序走訪 */
fun preOrder(root: TreeNode?) {
if (root == null) return
// 訪問優先順序:根節點 -> 左子樹 -> 右子樹
list.add(root.value)
preOrder(root.left)
preOrder(root.right)
}
/* 中序走訪 */
fun inOrder(root: TreeNode?) {
if (root == null) return
// 訪問優先順序:左子樹 -> 根節點 -> 右子樹
inOrder(root.left)
list.add(root.value)
inOrder(root.right)
}
/* 後序走訪 */
fun postOrder(root: TreeNode?) {
if (root == null) return
// 訪問優先順序:左子樹 -> 右子樹 -> 根節點
postOrder(root.left)
postOrder(root.right)
list.add(root.value)
}
binary_tree_dfs.zig
// 前序走訪
fn preOrder(comptime T: type, root: ?*inc.TreeNode(T)) !void {
if (root == null) return;
// 訪問優先順序:根節點 -> 左子樹 -> 右子樹
try list.append(root.?.val);
try preOrder(T, root.?.left);
try preOrder(T, root.?.right);
}
// 中序走訪
fn inOrder(comptime T: type, root: ?*inc.TreeNode(T)) !void {
if (root == null) return;
// 訪問優先順序:左子樹 -> 根節點 -> 右子樹
try inOrder(T, root.?.left);
try list.append(root.?.val);
try inOrder(T, root.?.right);
}
// 後序走訪
fn postOrder(comptime T: type, root: ?*inc.TreeNode(T)) !void {
if (root == null) return;
// 訪問優先順序:左子樹 -> 右子樹 -> 根節點
try postOrder(T, root.?.left);
try postOrder(T, root.?.right);
try list.append(root.?.val);
}
視覺化執行
Tip
深度優先搜尋也可以基於迭代實現,有興趣的讀者可以自行研究。
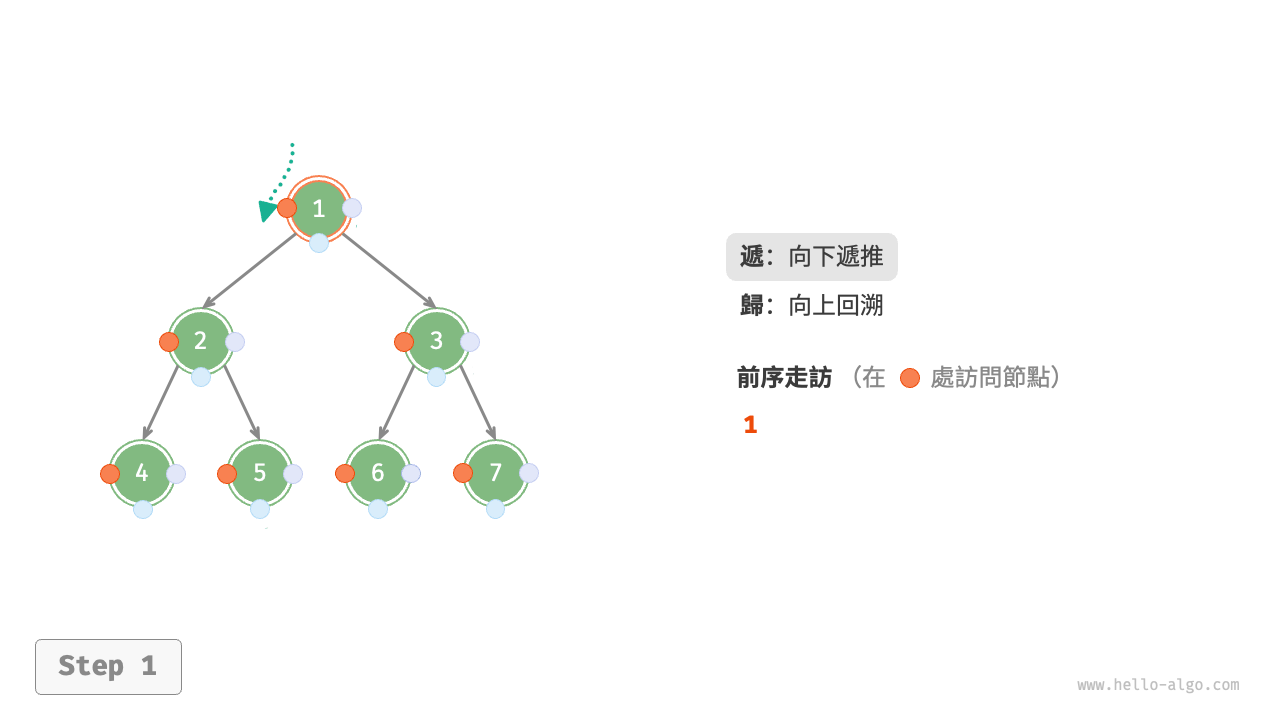
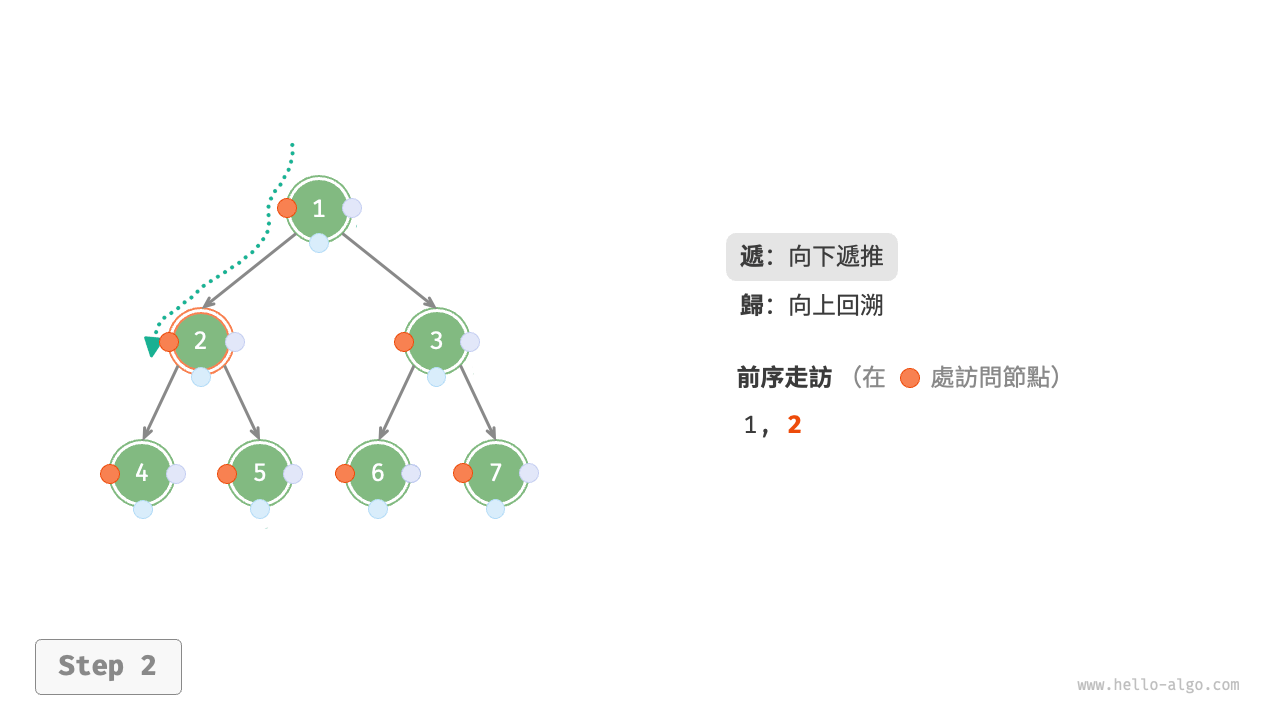
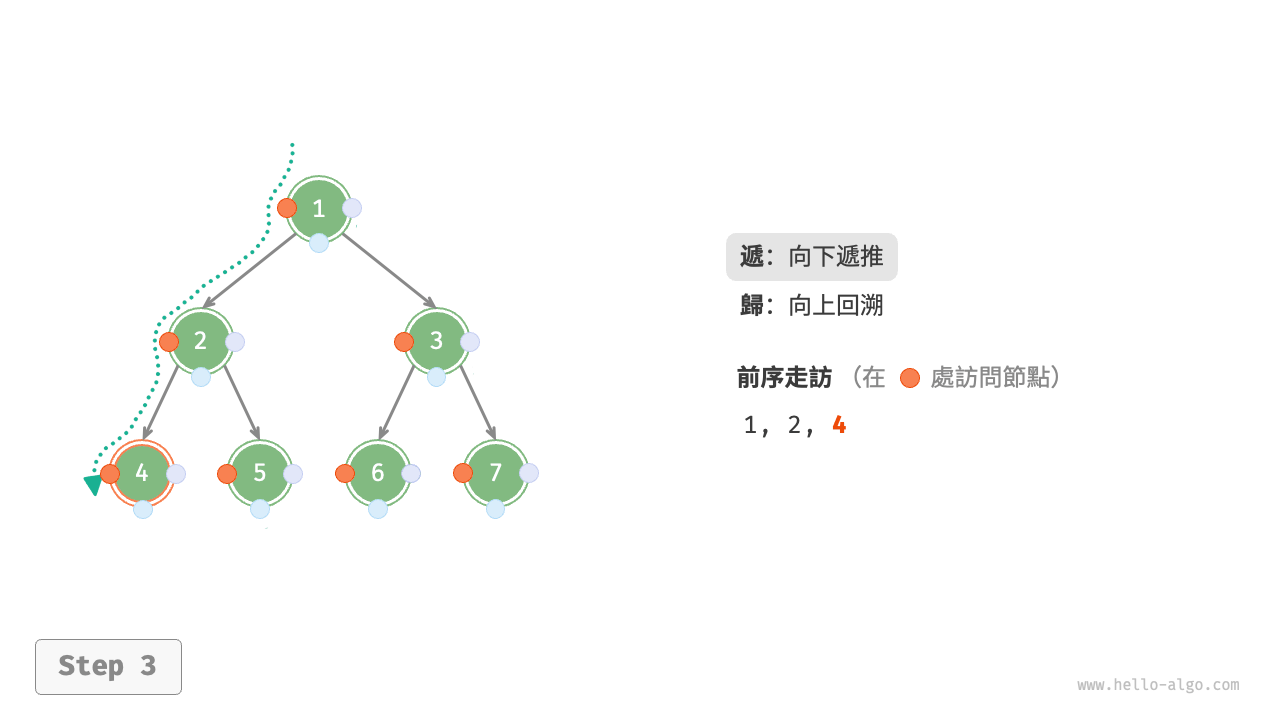
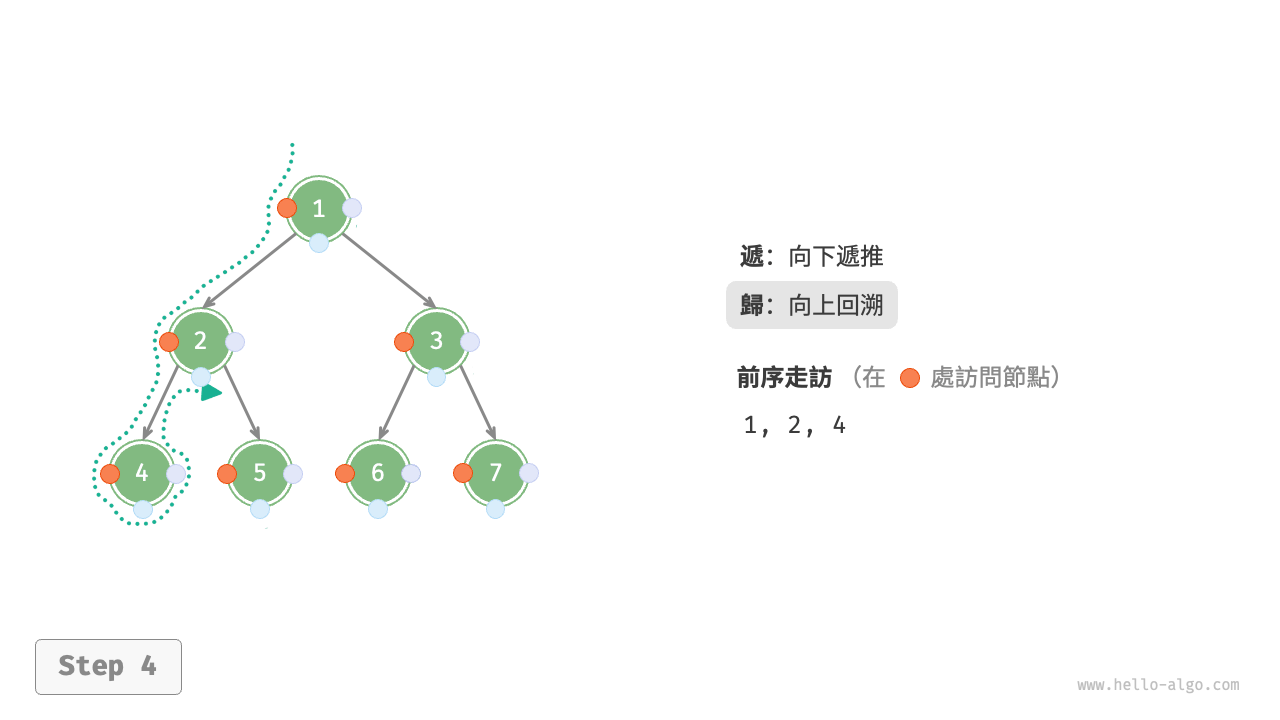
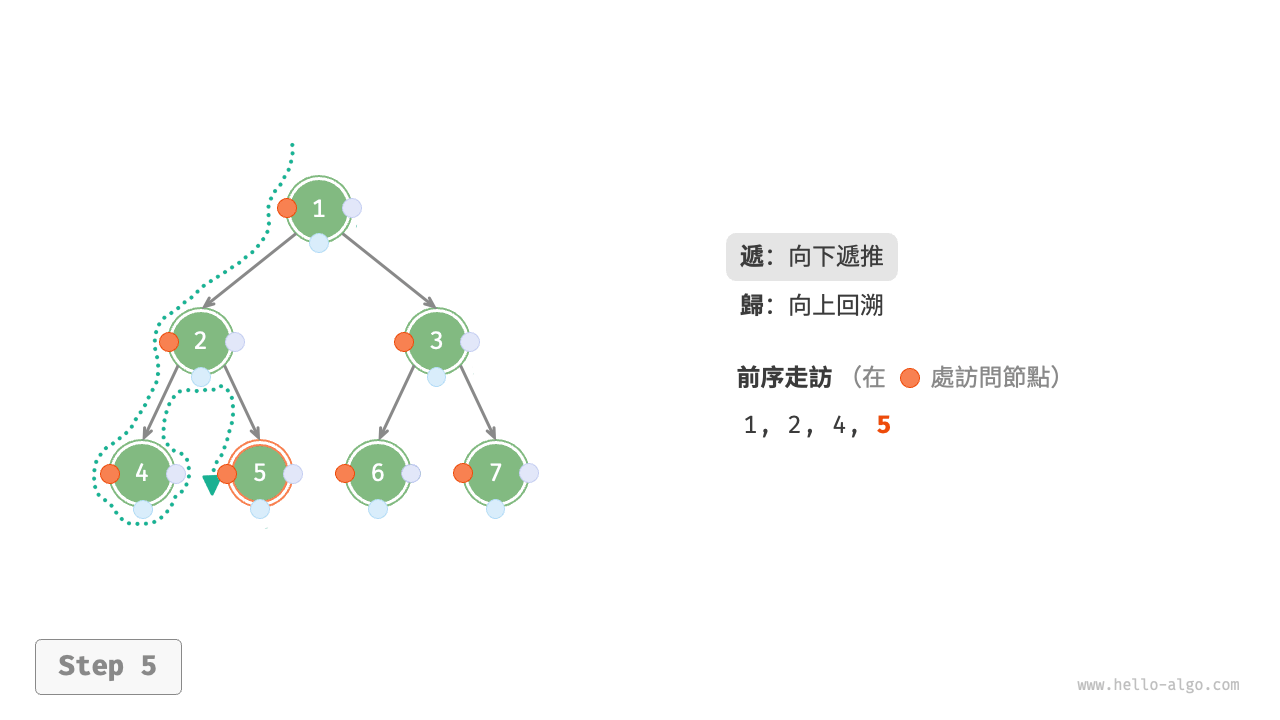
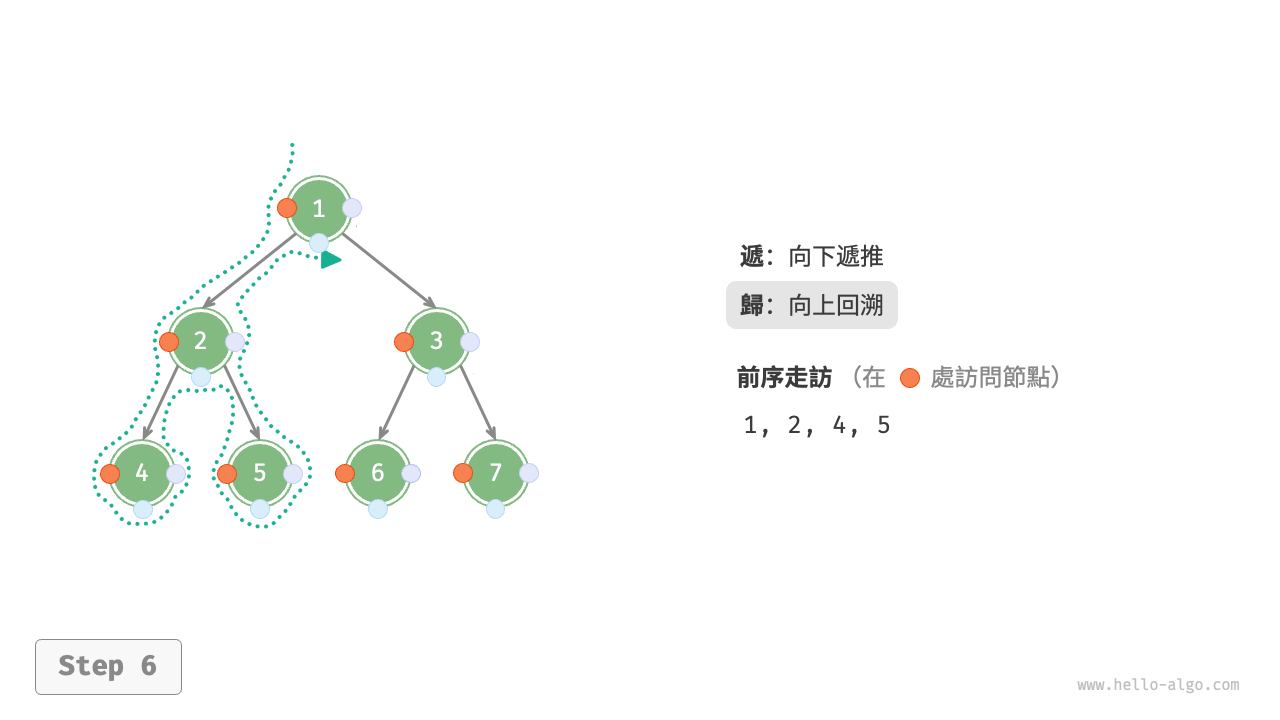
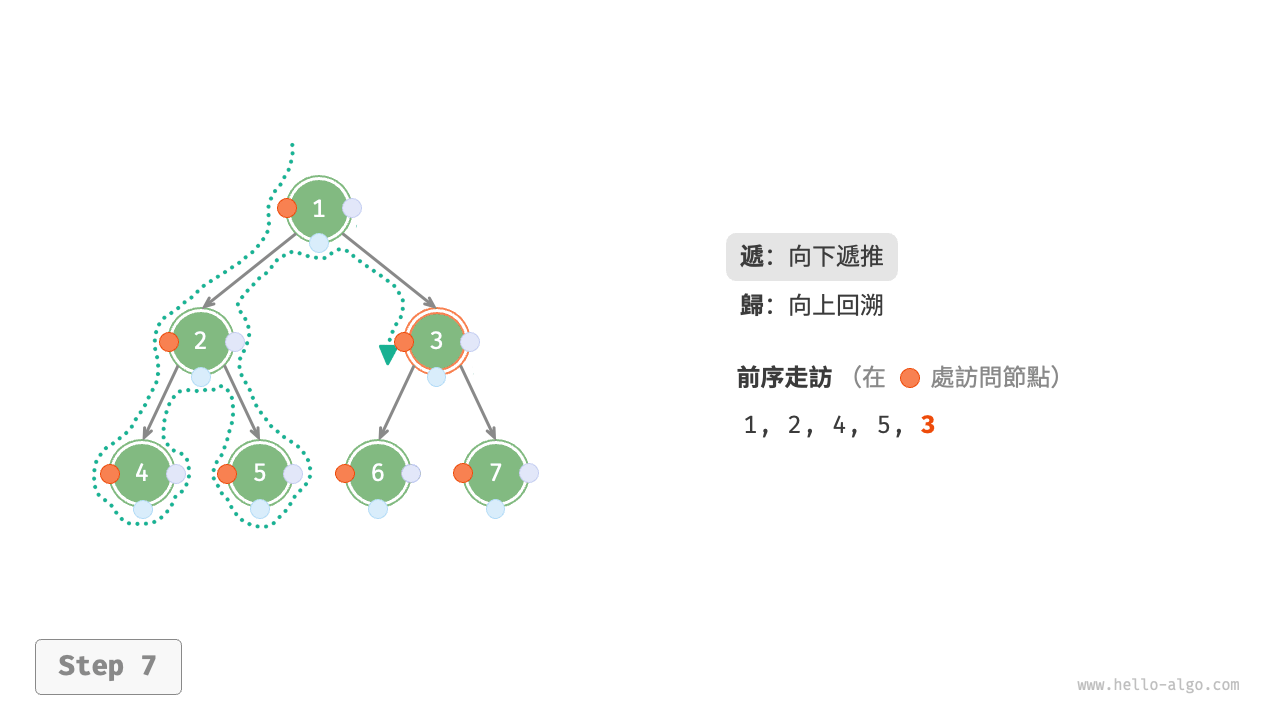
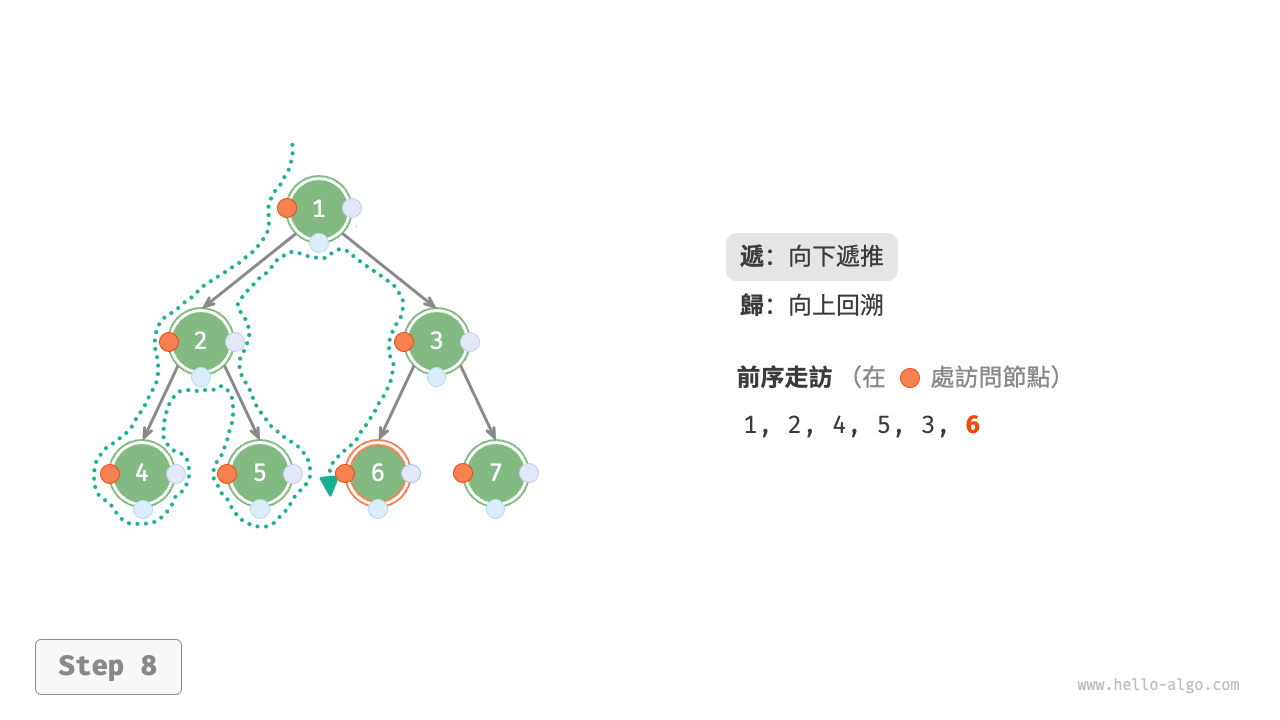
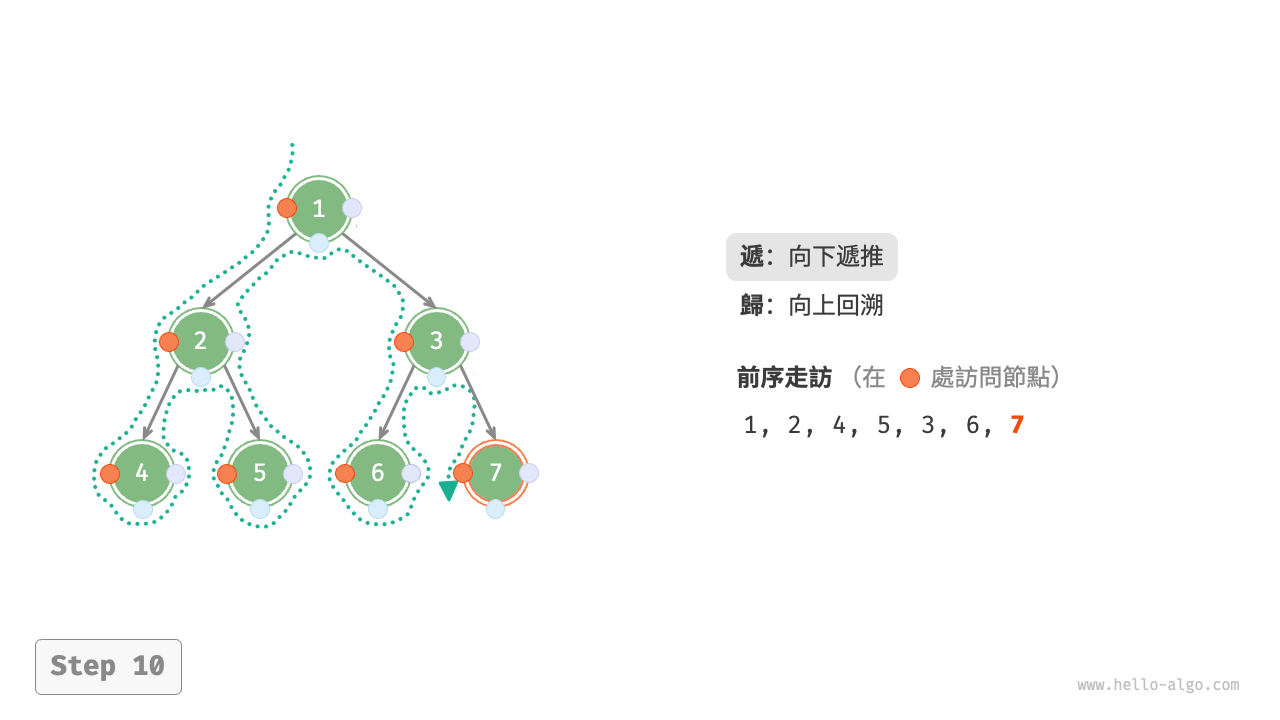
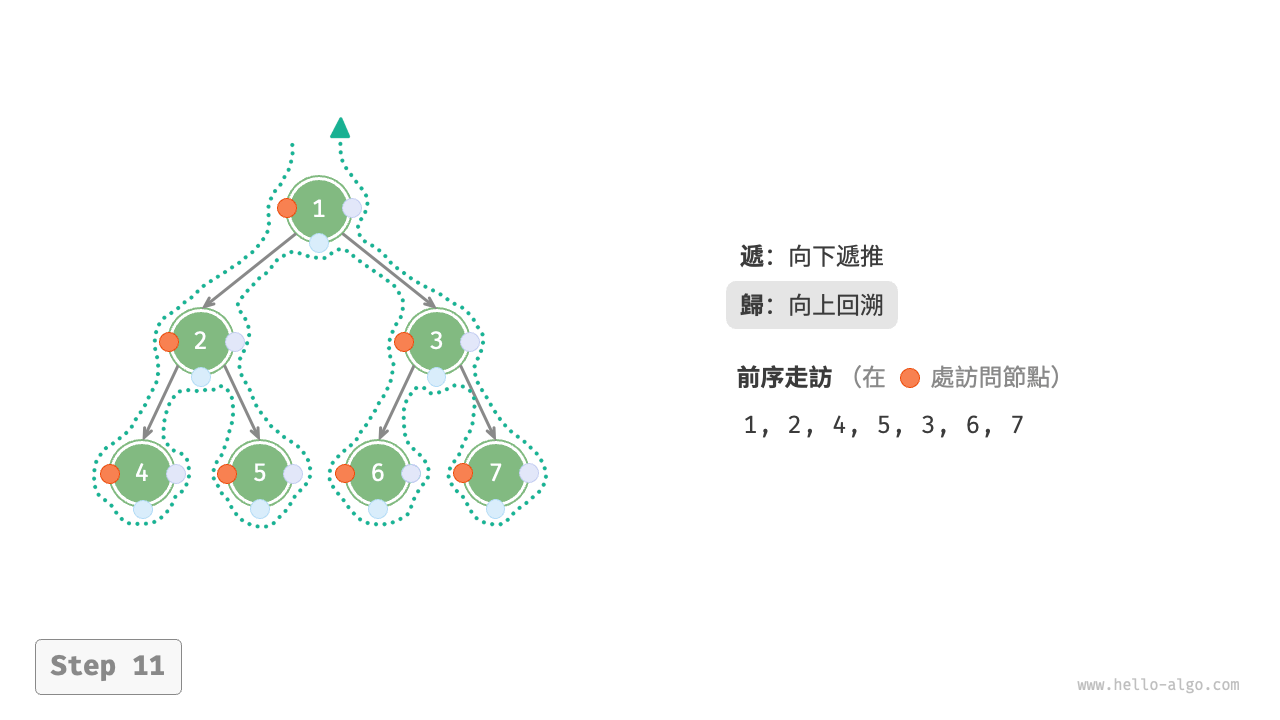
圖 7-11 展示了前序走訪二元樹的遞迴過程,其可分為“遞”和“迴”兩個逆向的部分。
- “遞”表示開啟新方法,程式在此過程中訪問下一個節點。
- “迴”表示函式返回,代表當前節點已經訪問完畢。
圖 7-11 前序走訪的遞迴過程
2. 複雜度分析¶
- 時間複雜度為 \(O(n)\) :所有節點被訪問一次,使用 \(O(n)\) 時間。
- 空間複雜度為 \(O(n)\) :在最差情況下,即樹退化為鏈結串列時,遞迴深度達到 \(n\) ,系統佔用 \(O(n)\) 堆疊幀空間。