13.3. 0-1 背包问题¶
背包问题是一个非常好的动态规划入门题目,是动态规划中最常见的问题形式。其具有很多变种,例如 0-1 背包问题、完全背包问题、多重背包问题等。
在本节中,我们先来学习基础的的 0-1 背包问题。
Question
给定 \(n\) 个物品,第 \(i\) 个物品的重量为 \(wgt[i-1]\) 、价值为 \(val[i-1]\) ,现在有个容量为 \(cap\) 的背包,请求解在不超过背包容量下背包中物品的最大价值。
请注意,物品编号 \(i\) 从 \(1\) 开始计数,数组索引从 \(0\) 开始计数,因此物品 \(i\) 对应重量 \(wgt[i-1]\) 和价值 \(val[i-1]\) 。
下图给出了一个 0-1 背包的示例数据,背包内的最大价值为 \(220\) 。
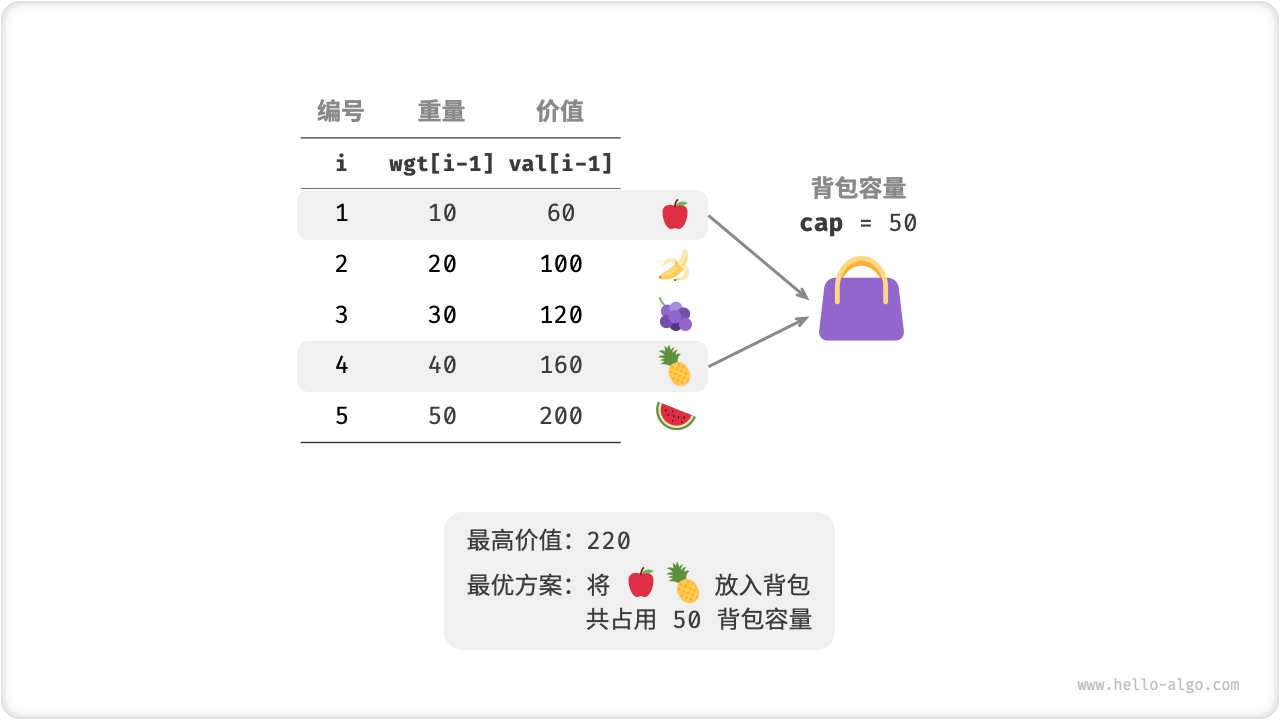
Fig. 0-1 背包的示例数据
在 0-1 背包问题中,每个物体都有不放入和放入两种决策。不放入背包,背包容量不变;放入背包,背包容量减小。由此可得:
- 状态包括物品编号 \(i\) 和背包容量 \(c\),记为 \([i, c]\) 。
- 状态 \([i, c]\) 对应子问题的解为:前 \(i\) 个物品在容量为 \(c\) 背包中的最大价值,记为 \(dp[i, c]\) 。
我们可以将 0-1 背包求解过程看作是一个由 \(n\) 轮决策组成的过程。从物品 \(n\) 开始,当我们做出物品 \(i\) 的决策后,剩余的是前 \(i-1\) 个物品的决策。因此,状态转移分为两种情况:
- 不放入物品 \(i\) :背包容量不变,状态转移至 \([i-1, c]\) ;
- 放入物品 \(i\) :背包容量减小 \(wgt[i-1]\) ,价值增加 \(val[i-1]\) ,状态转移至 \([i-1, c-wgt[i-1]]\) ;
上述的状态转移向我们展示了本题的「最优子结构」:最大价值 \(dp[i, c]\) 等于不放入物品 \(i\) 和放入物品 \(i\) 两种方案中的价值更大的那一个。由此可推出状态转移方程:
需要注意的是,若当前物品重量 \(wgt[i - 1]\) 超出剩余背包容量 \(c\) ,则只能选择不放入背包。
13.3.1. 方法一:暴力搜索¶
搜索代码包含以下要素:
- 递归参数:状态 \([i, c]\) ;返回值:子问题的解 \(dp[i, c]\) 。
- 终止条件:当物品编号越界 \(i = 0\) 或背包剩余容量为 \(0\) 时,终止递归并返回价值 \(0\) 。
- 剪枝:若当前物品重量 \(wgt[i - 1]\) 超出剩余背包容量 \(c\) ,则不能放入背包。
def knapsack_dfs(wgt, val, i, c):
"""0-1 背包:暴力搜索"""
# 若已选完所有物品或背包无容量,则返回价值 0
if i == 0 or c == 0:
return 0
# 若超过背包容量,则只能不放入背包
if wgt[i - 1] > c:
return knapsack_dfs(wgt, val, i - 1, c)
# 计算不放入和放入物品 i 的最大价值
no = knapsack_dfs(wgt, val, i - 1, c)
yes = knapsack_dfs(wgt, val, i - 1, c - wgt[i - 1]) + val[i - 1]
# 返回两种方案中价值更大的那一个
return max(no, yes)
如下图所示,由于每个物品都会产生不选和选两条搜索分支,因此最差时间复杂度为 \(O(2^n)\) 。
观察递归树,容易发现其中存在一些「重叠子问题」。而当物品较多、背包容量较大,尤其是当相同重量的物品较多时,重叠子问题的数量将会大幅增多。
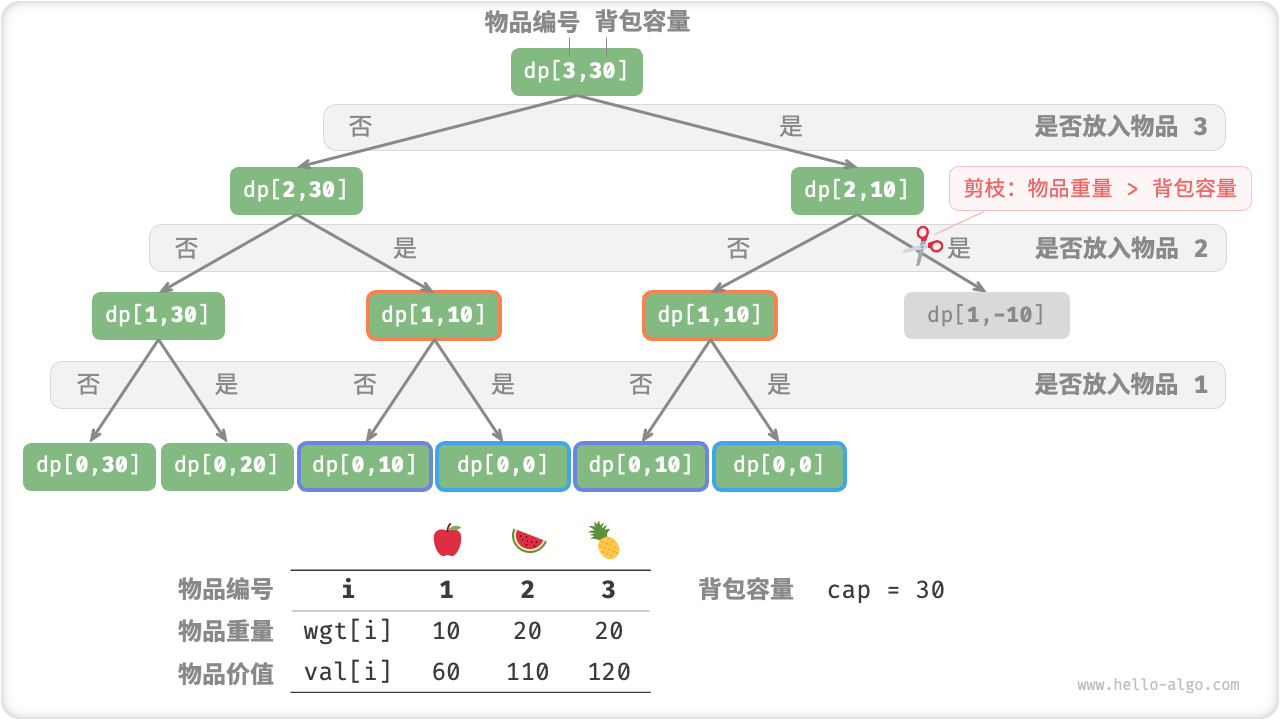
Fig. 0-1 背包的暴力搜索递归树
13.3.2. 方法二:记忆化搜索¶
为了防止重复求解重叠子问题,我们借助一个记忆列表 mem 来记录子问题的解,其中 mem[i][c] 记录解 \(dp[i, c]\) 。
def knapsack_dfs_mem(wgt, val, mem, i, c):
"""0-1 背包:记忆化搜索"""
# 若已选完所有物品或背包无容量,则返回价值 0
if i == 0 or c == 0:
return 0
# 若已有记录,则直接返回
if mem[i][c] != -1:
return mem[i][c]
# 若超过背包容量,则只能不放入背包
if wgt[i - 1] > c:
return knapsack_dfs_mem(wgt, val, mem, i - 1, c)
# 计算不放入和放入物品 i 的最大价值
no = knapsack_dfs_mem(wgt, val, mem, i - 1, c)
yes = knapsack_dfs_mem(wgt, val, mem, i - 1, c - wgt[i - 1]) + val[i - 1]
# 记录并返回两种方案中价值更大的那一个
mem[i][c] = max(no, yes)
return mem[i][c]
引入记忆化之后,所有子问题都只被计算一次,因此时间复杂度取决于子问题数量,也就是 \(O(n \times cap)\) 。
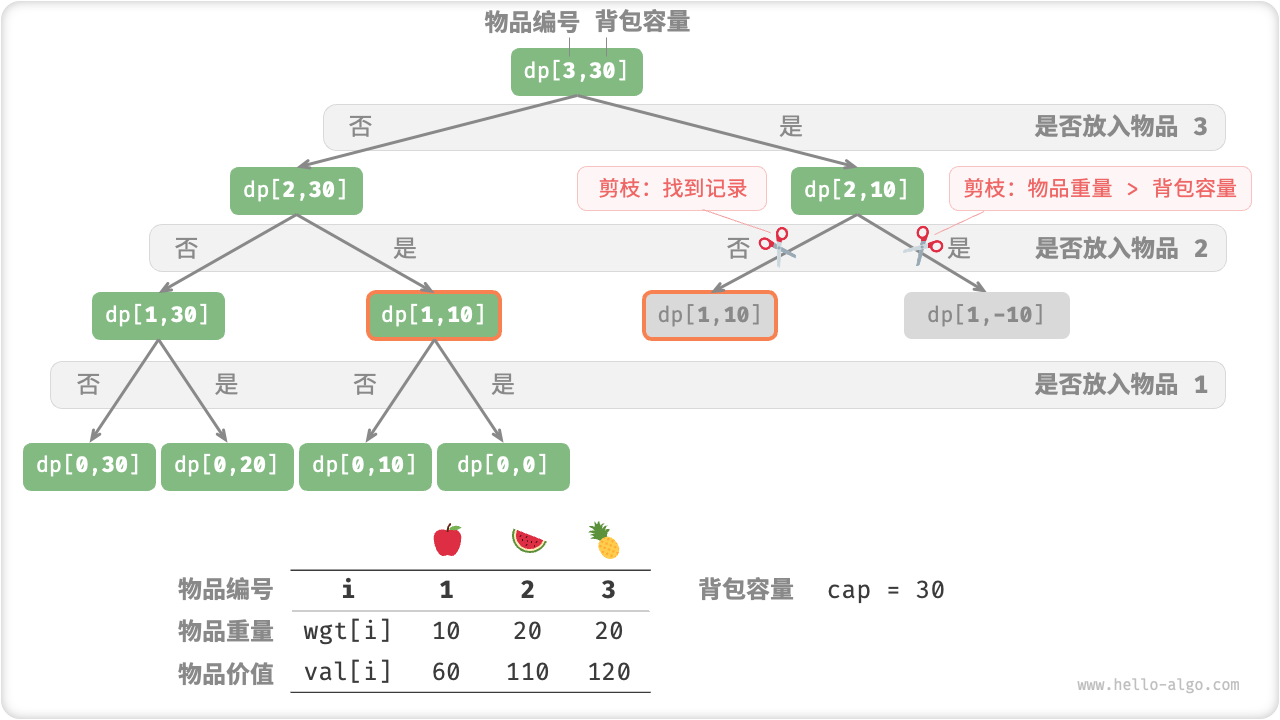
Fig. 0-1 背包的记忆化搜索递归树
13.3.3. 方法三:动态规划¶
接下来,我们将“从顶至底”的记忆化搜索代码译写为“从底至顶”的动态规划代码。
def knapsack_dp(wgt, val, cap):
"""0-1 背包:动态规划"""
n = len(wgt)
# 初始化 dp 列表
dp = [[0] * (cap + 1) for _ in range(n + 1)]
# 状态转移
for i in range(1, n + 1):
for c in range(1, cap + 1):
if wgt[i - 1] > c:
# 若超过背包容量,则不选物品 i
dp[i][c] = dp[i - 1][c]
else:
# 不选和选物品 i 这两种方案的较大值
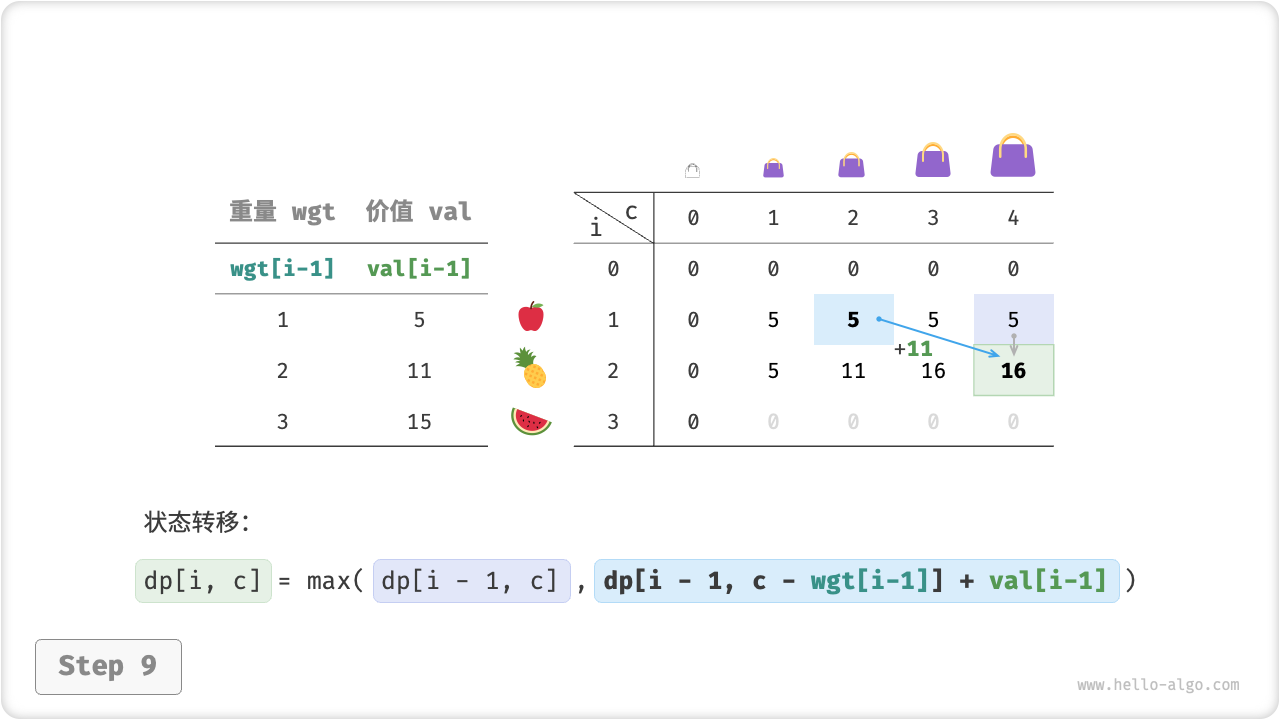
dp[i][c] = max(dp[i - 1][c - wgt[i - 1]] + val[i - 1], dp[i - 1][c])
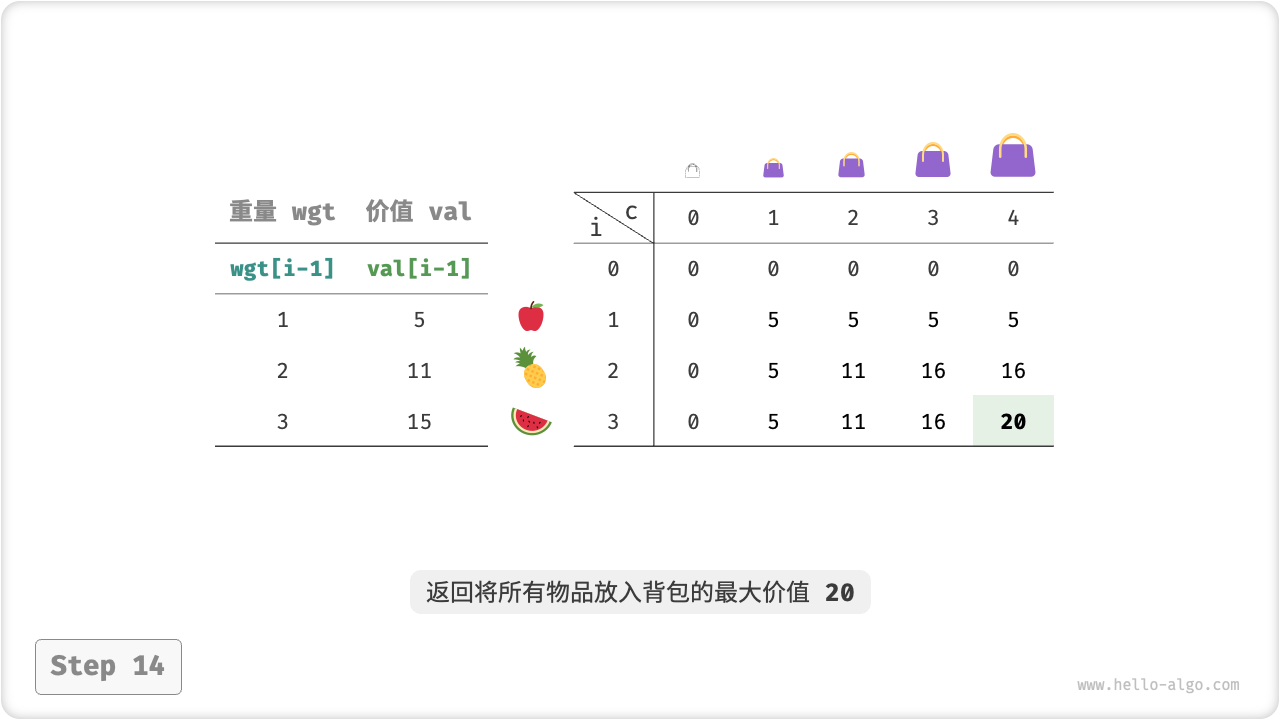
return dp[n][cap]
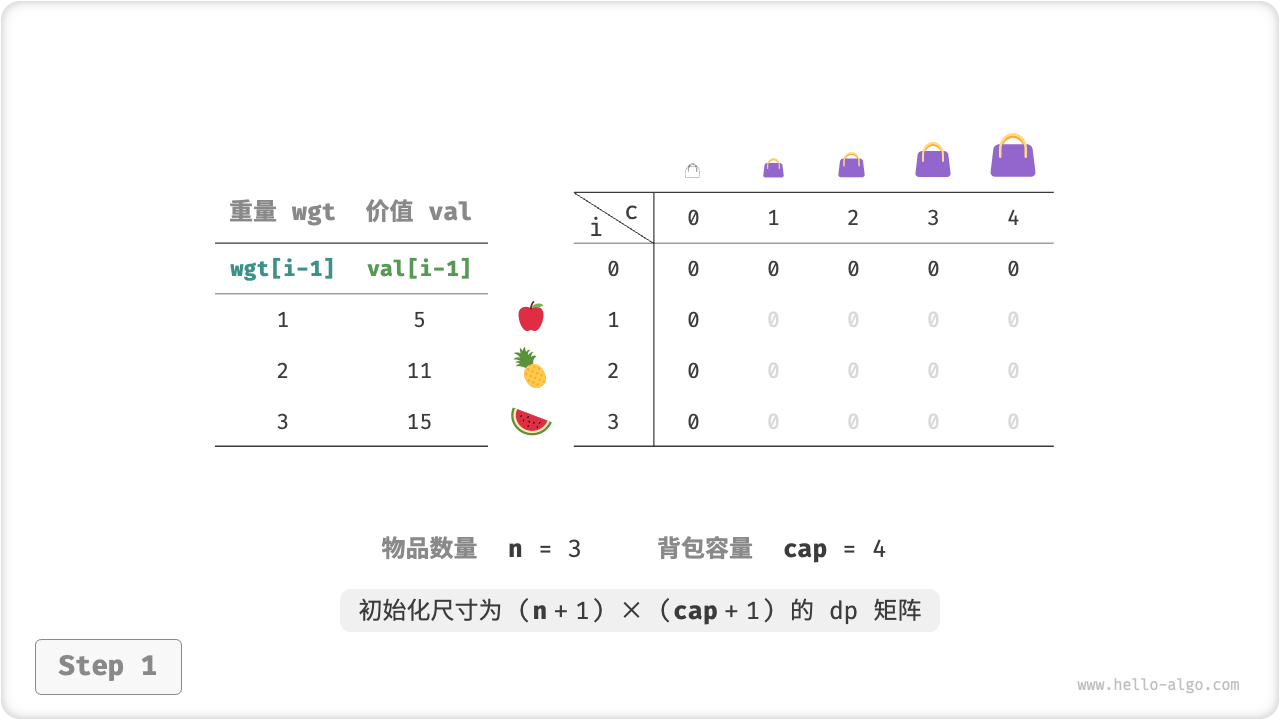
如下图所示,动态规划本质上就是填充 \(dp\) 矩阵的过程,时间复杂度也为 \(O(n \times cap)\) 。











最后考虑状态压缩。以上代码中的 \(dp\) 矩阵占用 \(O(n \times cap)\) 空间。由于每个状态都只与其上一行的状态有关,因此我们可以使用两个数组滚动前进,将空间复杂度从 \(O(n^2)\) 将低至 \(O(n)\) 。代码省略,有兴趣的同学可以自行实现。
那么,我们是否可以仅用一个数组实现状态压缩呢?观察可知,每个状态都是由左上方或正上方的格子转移过来的。假设只有一个数组,当遍历到第 \(i\) 行时,该数组存储的仍然是第 \(i-1\) 行的状态,为了避免左边区域的格子在状态转移中被覆盖,我们应采取倒序遍历。
以下动画展示了在单个数组下从第 \(i=1\) 行转换至第 \(i=2\) 行的过程。建议你思考一下正序遍历和倒序遍历的区别。

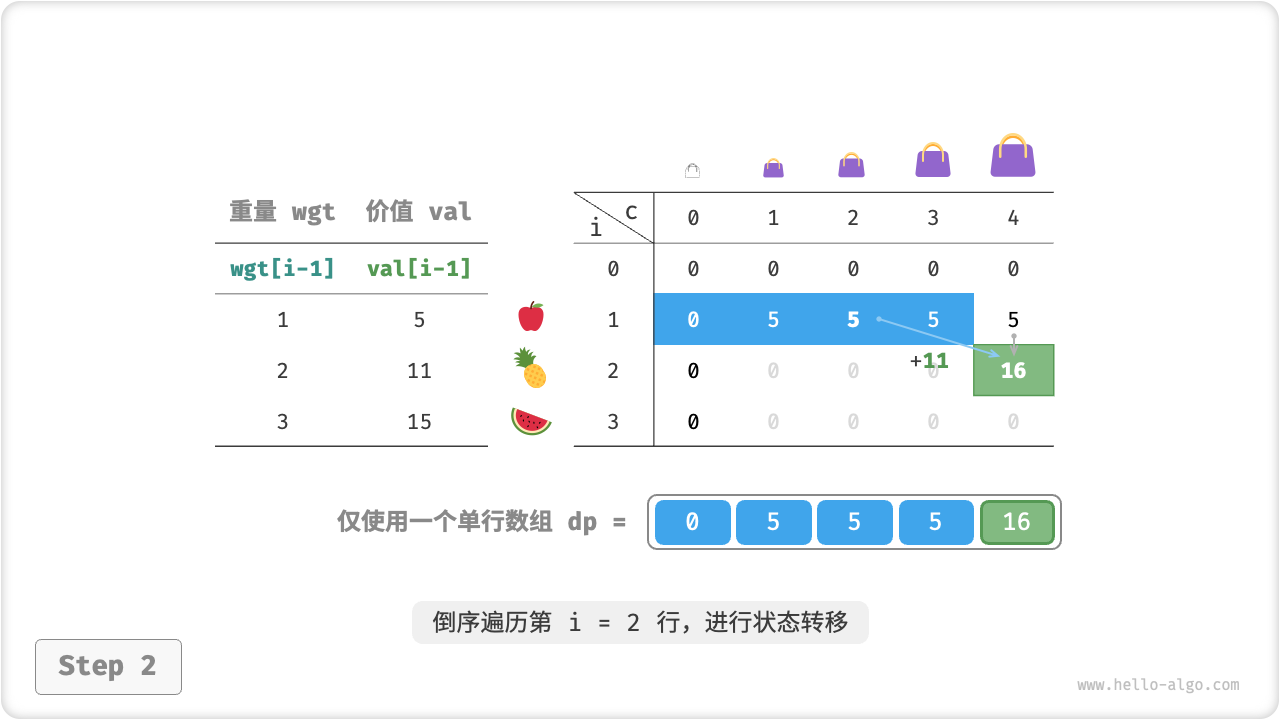



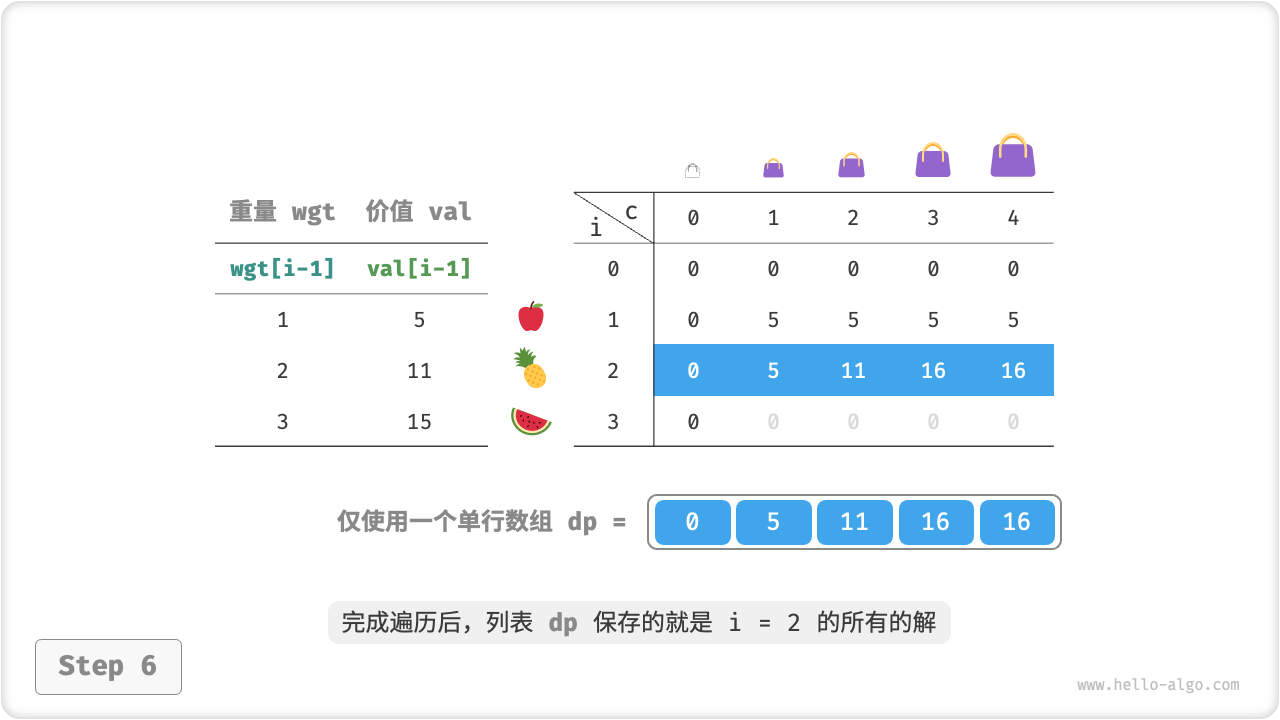
如以下代码所示,我们仅需将 \(dp\) 列表的第一维 \(i\) 直接删除,并且将内循环修改为倒序遍历即可。
def knapsack_dp_comp(wgt, val, cap):
"""0-1 背包:状态压缩后的动态规划"""
n = len(wgt)
# 初始化 dp 列表
dp = [0] * (cap + 1)
# 状态转移
for i in range(1, n + 1):
# 倒序遍历
for c in range(cap, 0, -1):
if wgt[i - 1] > c:
# 若超过背包容量,则不选物品 i
dp[c] = dp[c]
else:
# 不选和选物品 i 这两种方案的较大值
dp[c] = max(dp[c - wgt[i - 1]] + val[i - 1], dp[c])
return dp[cap]