13.2 Permutation problem¶
The permutation problem is a typical application of the backtracking algorithm. It is defined as finding all possible arrangements of elements from a given set (such as an array or string).
Table 13-2 lists several example data, including the input arrays and their corresponding permutations.
Table 13-2 Permutation examples
| Input array | Permutations |
|---|---|
| \([1]\) | \([1]\) |
| \([1, 2]\) | \([1, 2], [2, 1]\) |
| \([1, 2, 3]\) | \([1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2], [3, 2, 1]\) |
13.2.1 Cases without equal elements¶
Question
Enter an integer array without duplicate elements and return all possible permutations.
From the perspective of the backtracking algorithm, we can imagine the process of generating permutations as a series of choices. Suppose the input array is \([1, 2, 3]\), if we first choose \(1\), then \(3\), and finally \(2\), we obtain the permutation \([1, 3, 2]\). Backtracking means undoing a choice and then continuing to try other choices.
From the code perspective, the candidate set choices contains all elements of the input array, and the state state contains elements that have been selected so far. Please note that each element can only be chosen once, thus all elements in state must be unique.
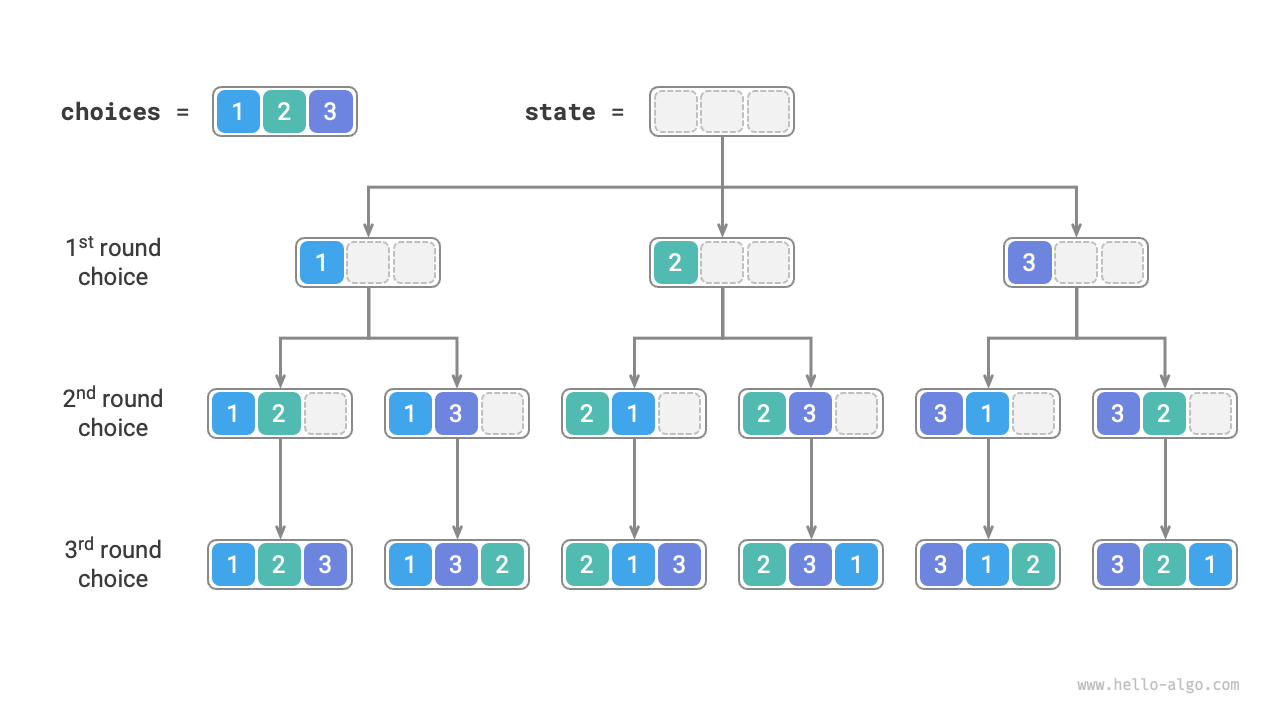
As shown in Figure 13-5, we can unfold the search process into a recursive tree, where each node represents the current state state. Starting from the root node, after three rounds of choices, we reach the leaf nodes, each corresponding to a permutation.
Figure 13-5 Permutation recursive tree
1. Pruning of repeated choices¶
To ensure that each element is selected only once, we consider introducing a boolean array selected, where selected[i] indicates whether choices[i] has been selected. We base our pruning operations on this array:
- After making the choice
choice[i], we setselected[i]to \(\text{True}\), indicating it has been chosen. - When iterating through the choice list
choices, skip all nodes that have already been selected, i.e., prune.
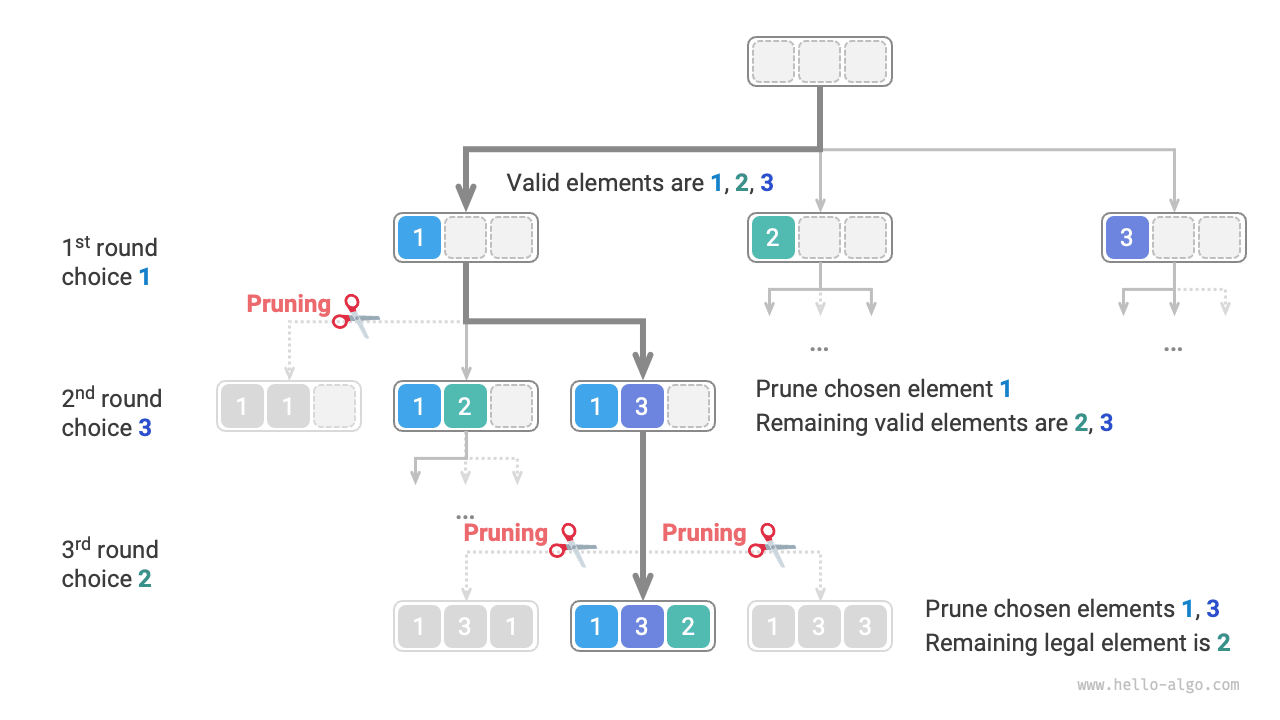
As shown in Figure 13-6, suppose we choose 1 in the first round, 3 in the second round, and 2 in the third round, we need to prune the branch of element 1 in the second round and elements 1 and 3 in the third round.
Figure 13-6 Permutation pruning example
Observing Figure 13-6, this pruning operation reduces the search space size from \(O(n^n)\) to \(O(n!)\).
2. Code implementation¶
After understanding the above information, we can "fill in the blanks" in the framework code. To shorten the overall code, we do not implement individual functions within the framework code separately, but expand them in the backtrack() function:
def backtrack(
state: list[int], choices: list[int], selected: list[bool], res: list[list[int]]
):
"""Backtracking algorithm: Permutation I"""
# When the state length equals the number of elements, record the solution
if len(state) == len(choices):
res.append(list(state))
return
# Traverse all choices
for i, choice in enumerate(choices):
# Pruning: do not allow repeated selection of elements
if not selected[i]:
# Attempt: make a choice, update the state
selected[i] = True
state.append(choice)
# Proceed to the next round of selection
backtrack(state, choices, selected, res)
# Retract: undo the choice, restore to the previous state
selected[i] = False
state.pop()
def permutations_i(nums: list[int]) -> list[list[int]]:
"""Permutation I"""
res = []
backtrack(state=[], choices=nums, selected=[False] * len(nums), res=res)
return res
/* Backtracking algorithm: Permutation I */
void backtrack(List<Integer> state, int[] choices, boolean[] selected, List<List<Integer>> res) {
// When the state length equals the number of elements, record the solution
if (state.size() == choices.length) {
res.add(new ArrayList<Integer>(state));
return;
}
// Traverse all choices
for (int i = 0; i < choices.length; i++) {
int choice = choices[i];
// Pruning: do not allow repeated selection of elements
if (!selected[i]) {
// Attempt: make a choice, update the state
selected[i] = true;
state.add(choice);
// Proceed to the next round of selection
backtrack(state, choices, selected, res);
// Retract: undo the choice, restore to the previous state
selected[i] = false;
state.remove(state.size() - 1);
}
}
}
/* Permutation I */
List<List<Integer>> permutationsI(int[] nums) {
List<List<Integer>> res = new ArrayList<List<Integer>>();
backtrack(new ArrayList<Integer>(), nums, new boolean[nums.length], res);
return res;
}
13.2.2 Considering cases with equal elements¶
Question
Enter an integer array, which may contain duplicate elements, and return all unique permutations.
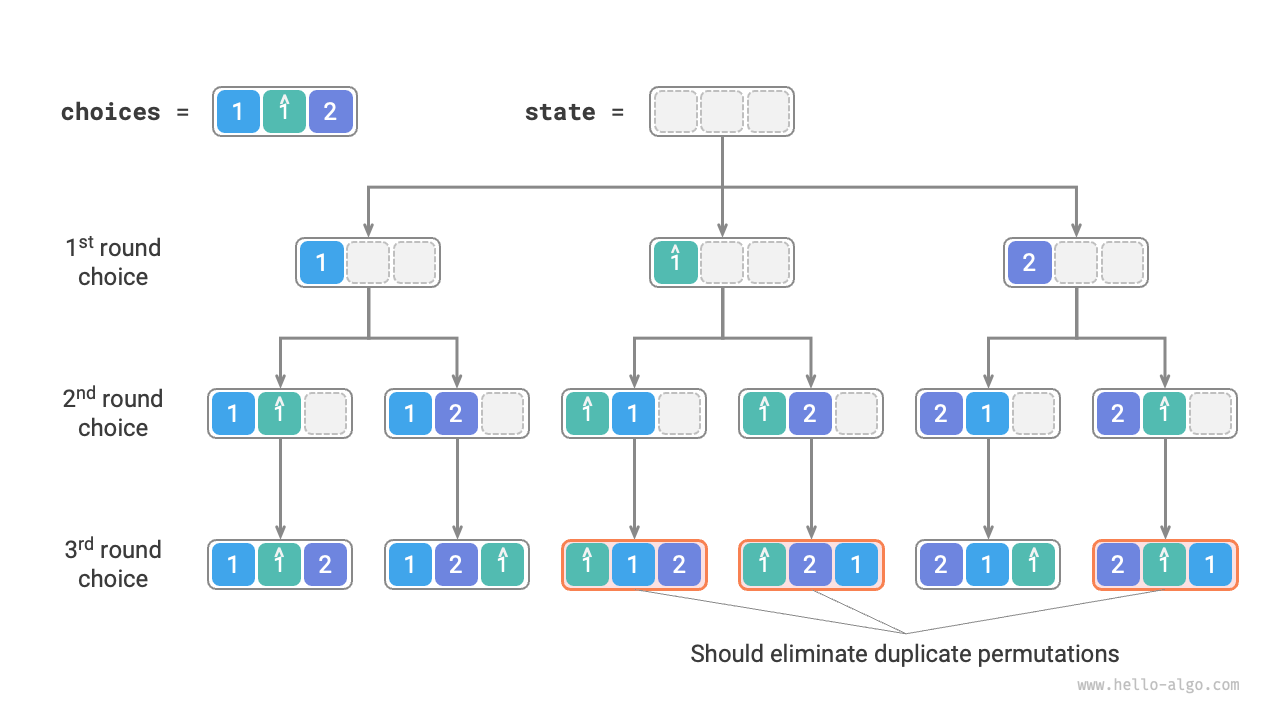
Suppose the input array is \([1, 1, 2]\). To differentiate the two duplicate elements \(1\), we mark the second \(1\) as \(\hat{1}\).
As shown in Figure 13-7, half of the permutations generated by the above method are duplicates.
Figure 13-7 Duplicate permutations
So, how do we eliminate duplicate permutations? Most directly, consider using a hash set to deduplicate permutation results. However, this is not elegant, as branches generating duplicate permutations are unnecessary and should be identified and pruned in advance, which can further improve algorithm efficiency.
1. Pruning of equal elements¶
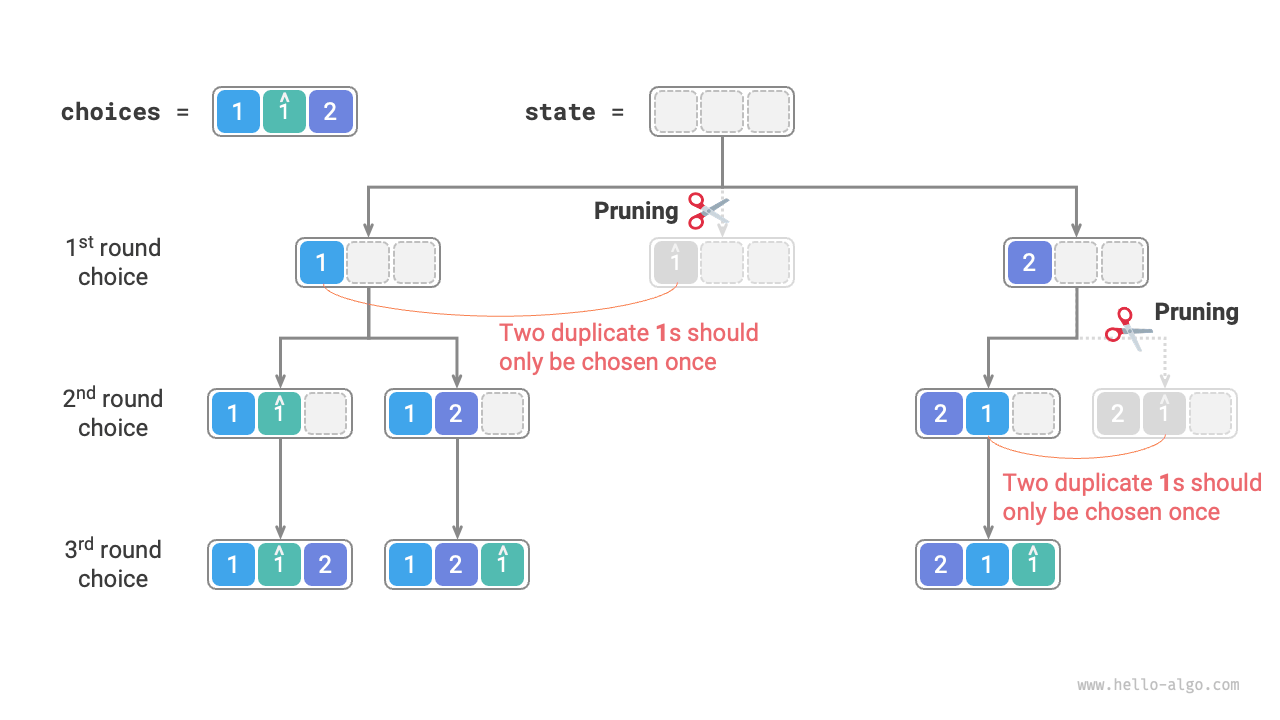
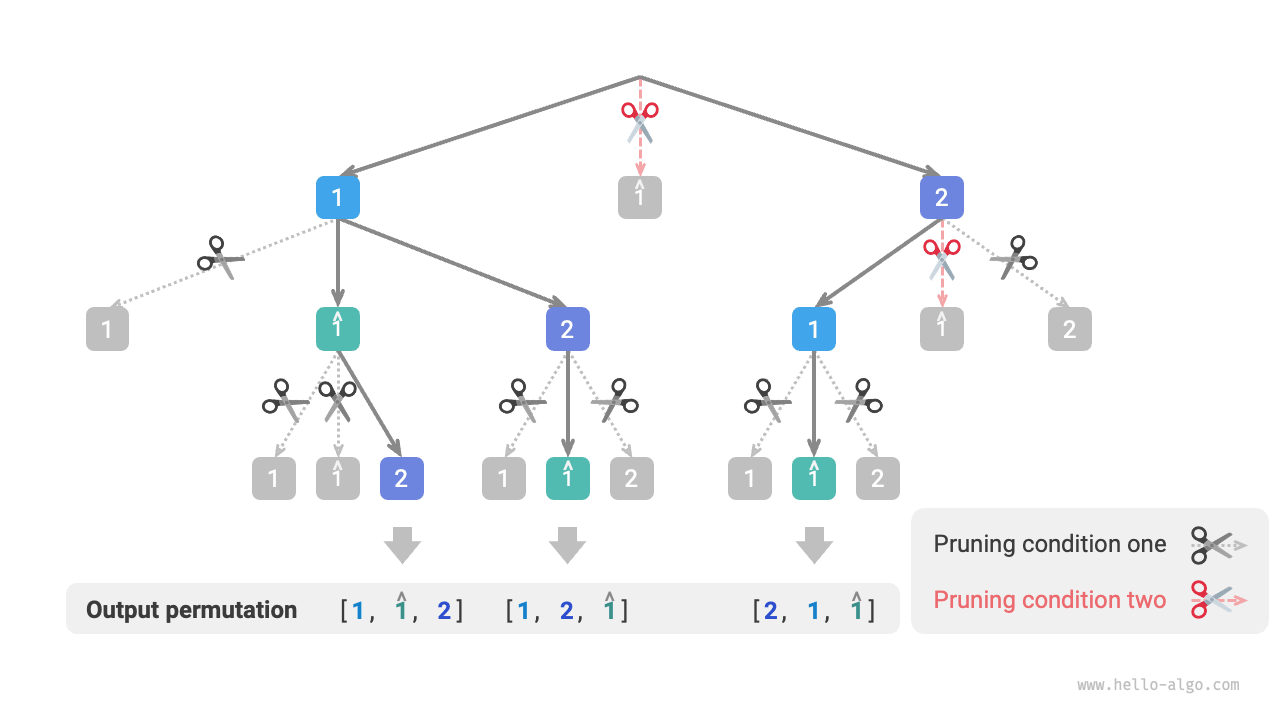
Observing Figure 13-8, in the first round, choosing \(1\) or \(\hat{1}\) results in identical permutations under both choices, thus we should prune \(\hat{1}\).
Similarly, after choosing \(2\) in the first round, choosing \(1\) and \(\hat{1}\) in the second round also produces duplicate branches, so we should also prune \(\hat{1}\) in the second round.
Essentially, our goal is to ensure that multiple equal elements are only selected once in each round of choices.
Figure 13-8 Duplicate permutations pruning
2. Code implementation¶
Based on the code from the previous problem, we consider initiating a hash set duplicated in each round of choices, used to record elements that have been tried in that round, and prune duplicate elements:
def backtrack(
state: list[int], choices: list[int], selected: list[bool], res: list[list[int]]
):
"""Backtracking algorithm: Permutation II"""
# When the state length equals the number of elements, record the solution
if len(state) == len(choices):
res.append(list(state))
return
# Traverse all choices
duplicated = set[int]()
for i, choice in enumerate(choices):
# Pruning: do not allow repeated selection of elements and do not allow repeated selection of equal elements
if not selected[i] and choice not in duplicated:
# Attempt: make a choice, update the state
duplicated.add(choice) # Record selected element values
selected[i] = True
state.append(choice)
# Proceed to the next round of selection
backtrack(state, choices, selected, res)
# Retract: undo the choice, restore to the previous state
selected[i] = False
state.pop()
def permutations_ii(nums: list[int]) -> list[list[int]]:
"""Permutation II"""
res = []
backtrack(state=[], choices=nums, selected=[False] * len(nums), res=res)
return res
/* Backtracking algorithm: Permutation II */
void backtrack(List<Integer> state, int[] choices, boolean[] selected, List<List<Integer>> res) {
// When the state length equals the number of elements, record the solution
if (state.size() == choices.length) {
res.add(new ArrayList<Integer>(state));
return;
}
// Traverse all choices
Set<Integer> duplicated = new HashSet<Integer>();
for (int i = 0; i < choices.length; i++) {
int choice = choices[i];
// Pruning: do not allow repeated selection of elements and do not allow repeated selection of equal elements
if (!selected[i] && !duplicated.contains(choice)) {
// Attempt: make a choice, update the state
duplicated.add(choice); // Record selected element values
selected[i] = true;
state.add(choice);
// Proceed to the next round of selection
backtrack(state, choices, selected, res);
// Retract: undo the choice, restore to the previous state
selected[i] = false;
state.remove(state.size() - 1);
}
}
}
/* Permutation II */
List<List<Integer>> permutationsII(int[] nums) {
List<List<Integer>> res = new ArrayList<List<Integer>>();
backtrack(new ArrayList<Integer>(), nums, new boolean[nums.length], res);
return res;
}
Assuming all elements are distinct from each other, there are \(n!\) (factorial) permutations of \(n\) elements; when recording results, it is necessary to copy a list of length \(n\), using \(O(n)\) time. Thus, the time complexity is \(O(n!n)\).
The maximum recursion depth is \(n\), using \(O(n)\) frame space. Selected uses \(O(n)\) space. At any one time, there can be up to \(n\) duplicated, using \(O(n^2)\) space. Therefore, the space complexity is \(O(n^2)\).
3. Comparison of the two pruning methods¶
Please note, although both selected and duplicated are used for pruning, their targets are different.
- Repeated choice pruning: There is only one
selectedthroughout the search process. It records which elements are currently in the state, aiming to prevent an element from appearing repeatedly instate. - Equal element pruning: Each round of choices (each call to the
backtrackfunction) contains aduplicated. It records which elements have been chosen in the current traversal (forloop), aiming to ensure equal elements are selected only once.
Figure 13-9 shows the scope of the two pruning conditions. Note, each node in the tree represents a choice, and the nodes from the root to the leaf form a permutation.
Figure 13-9 Scope of the two pruning conditions