10.1 Binary search¶
Binary search is an efficient search algorithm based on the divide-and-conquer strategy. It utilizes the orderliness of data, reducing the search range by half each round until the target element is found or the search interval is empty.
Question
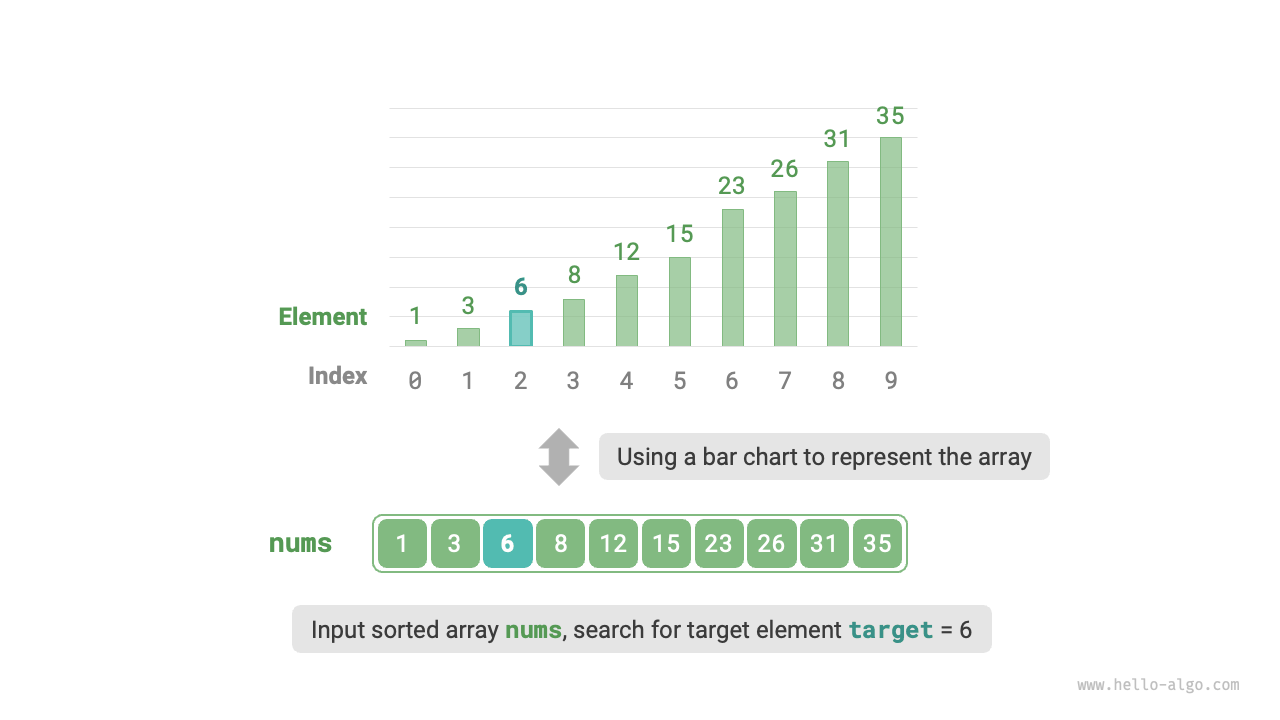
Given an array nums of length \(n\), with elements arranged in ascending order and non-repeating. Please find and return the index of element target in this array. If the array does not contain the element, return \(-1\). An example is shown in Figure 10-1.
Figure 10-1 Binary search example data
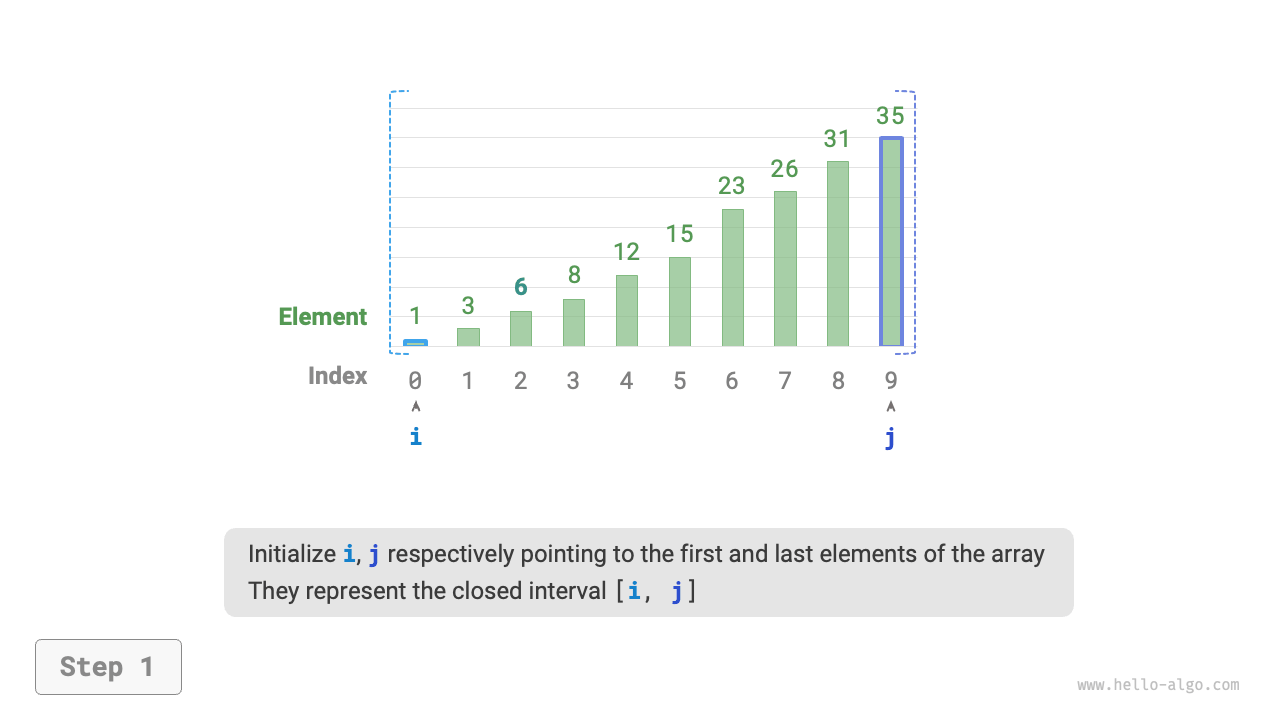
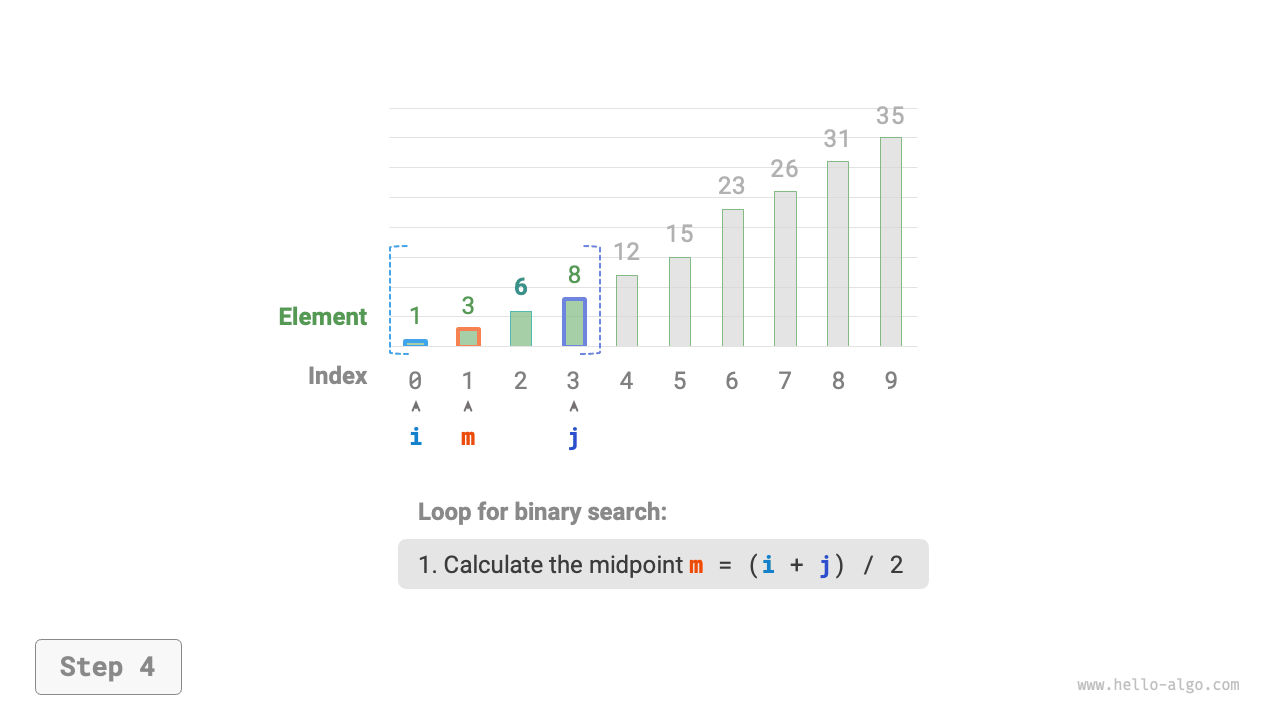
As shown in Figure 10-2, we first initialize pointers \(i = 0\) and \(j = n - 1\), pointing to the first and last elements of the array, representing the search interval \([0, n - 1]\). Please note that square brackets indicate a closed interval, which includes the boundary values themselves.
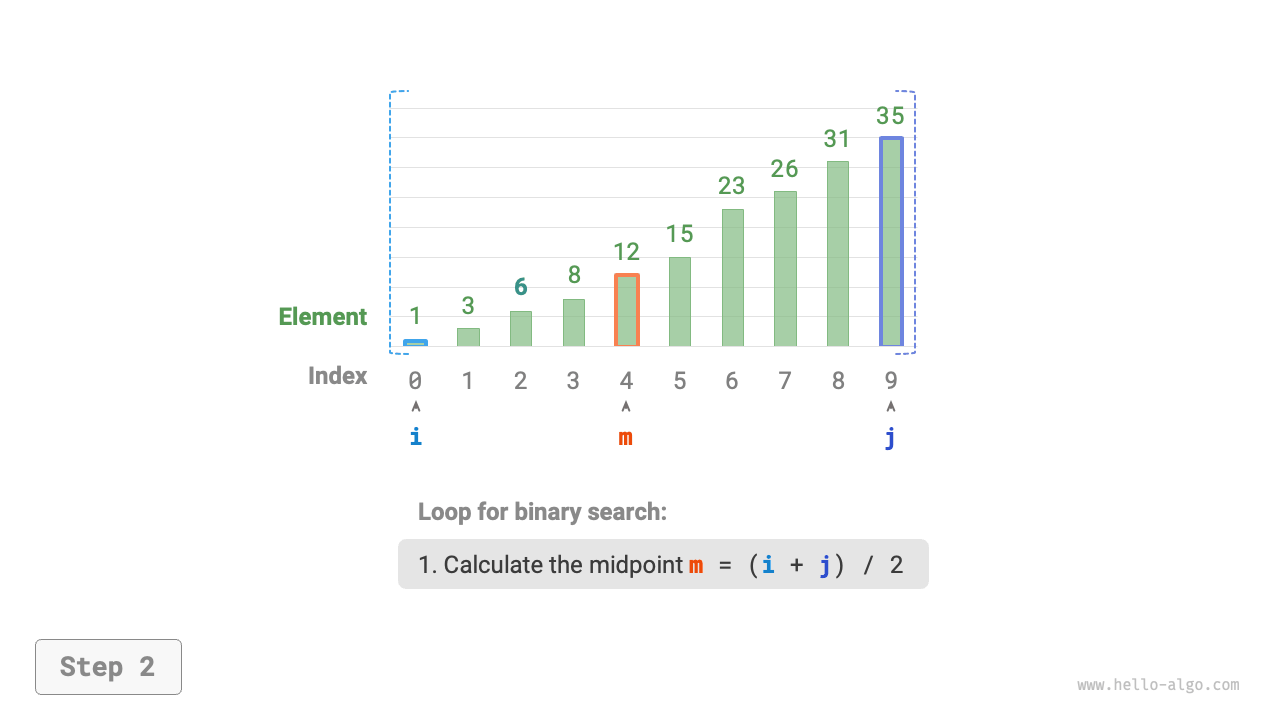
Next, perform the following two steps in a loop.
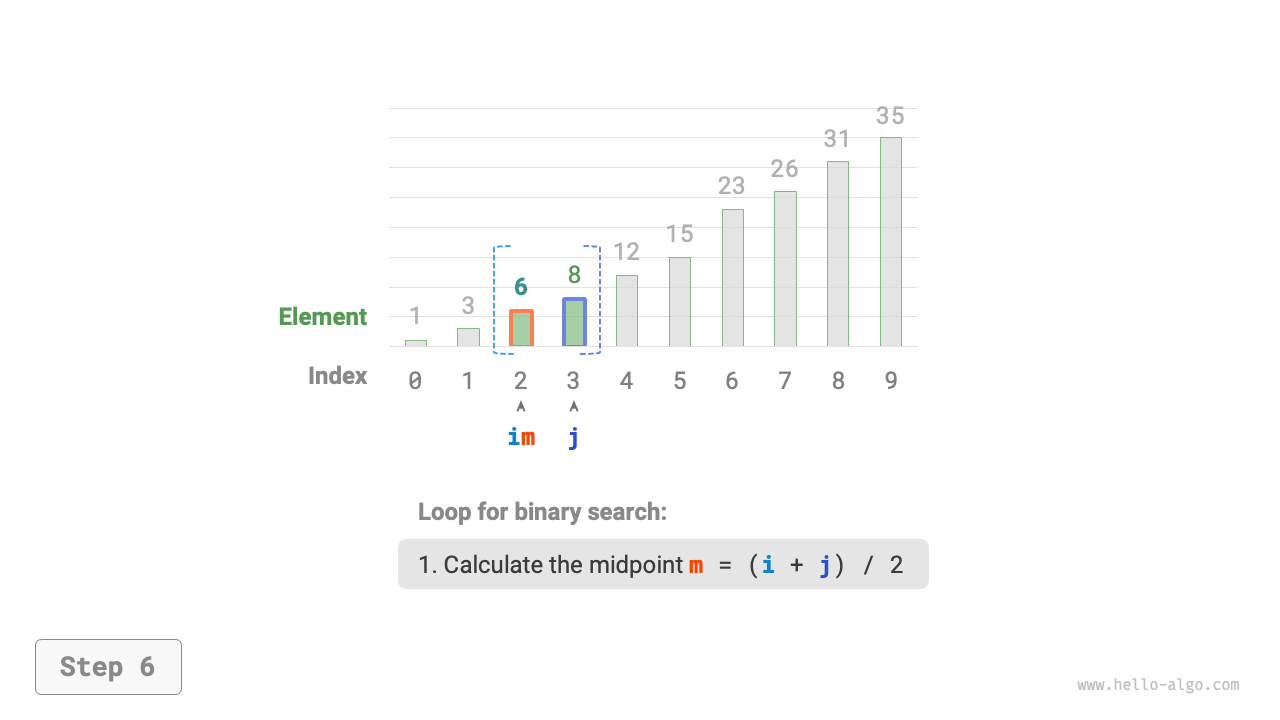
- Calculate the midpoint index \(m = \lfloor {(i + j) / 2} \rfloor\), where \(\lfloor \: \rfloor\) denotes the floor operation.
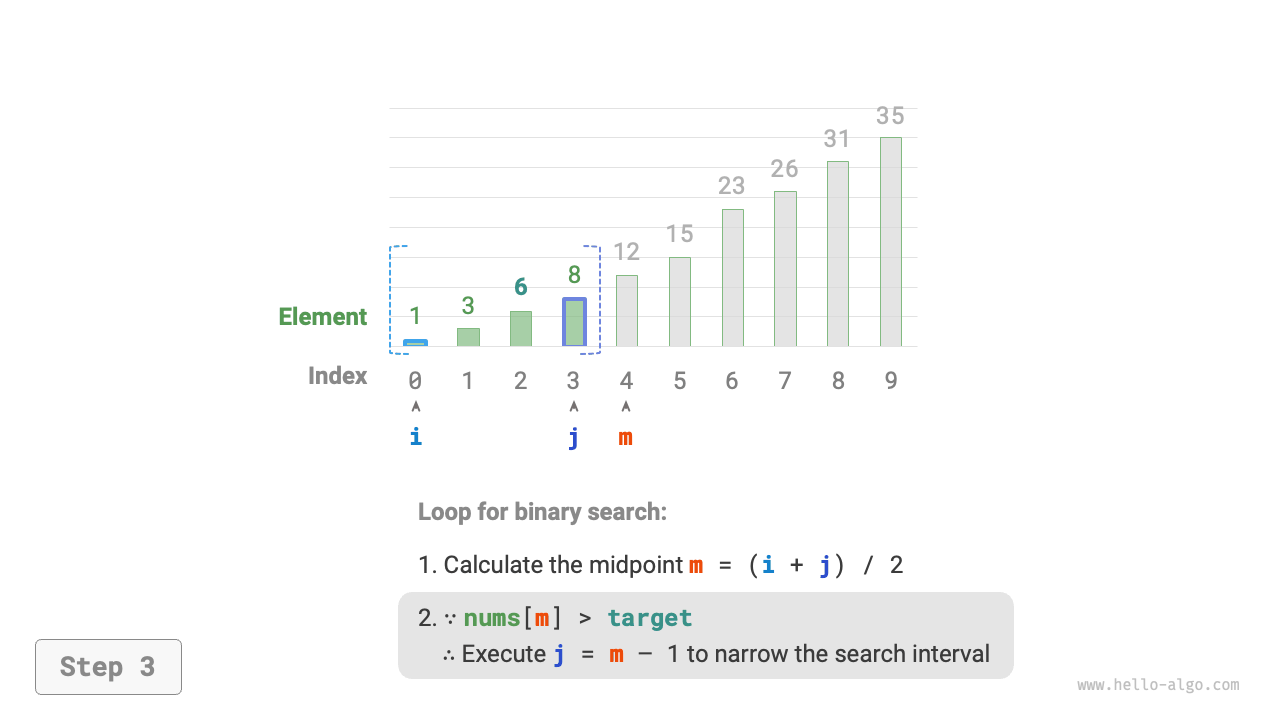
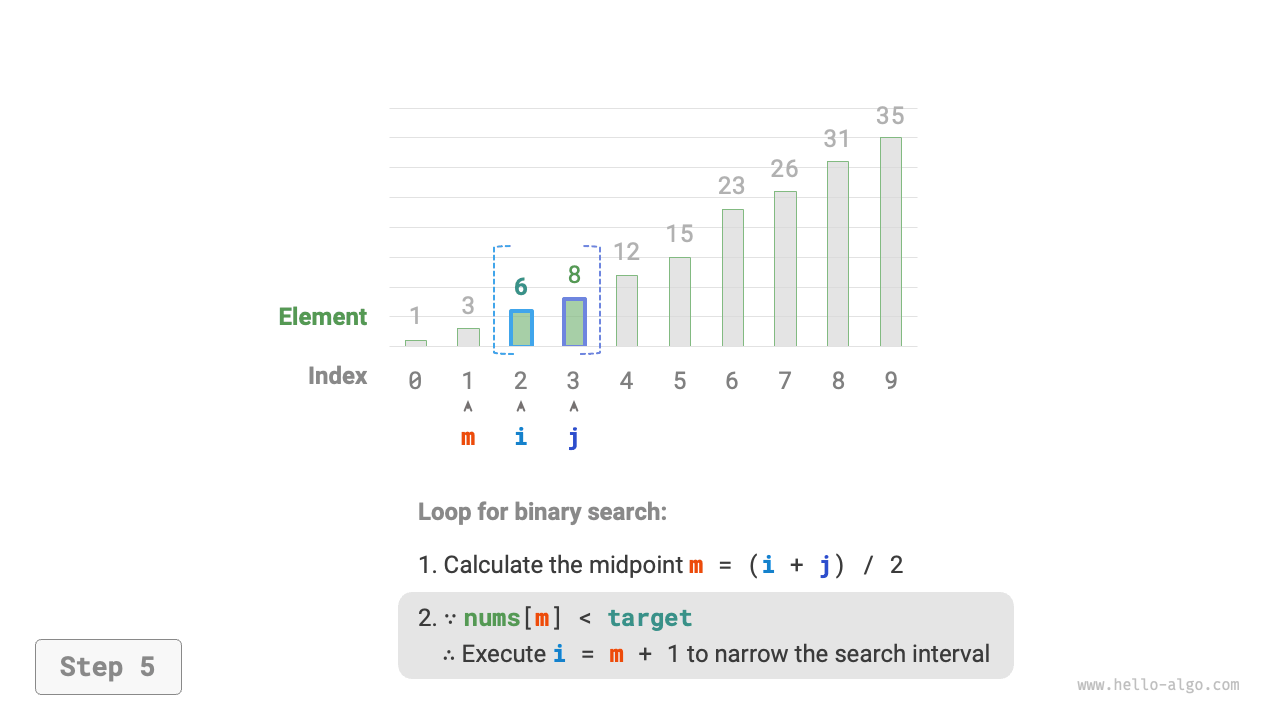
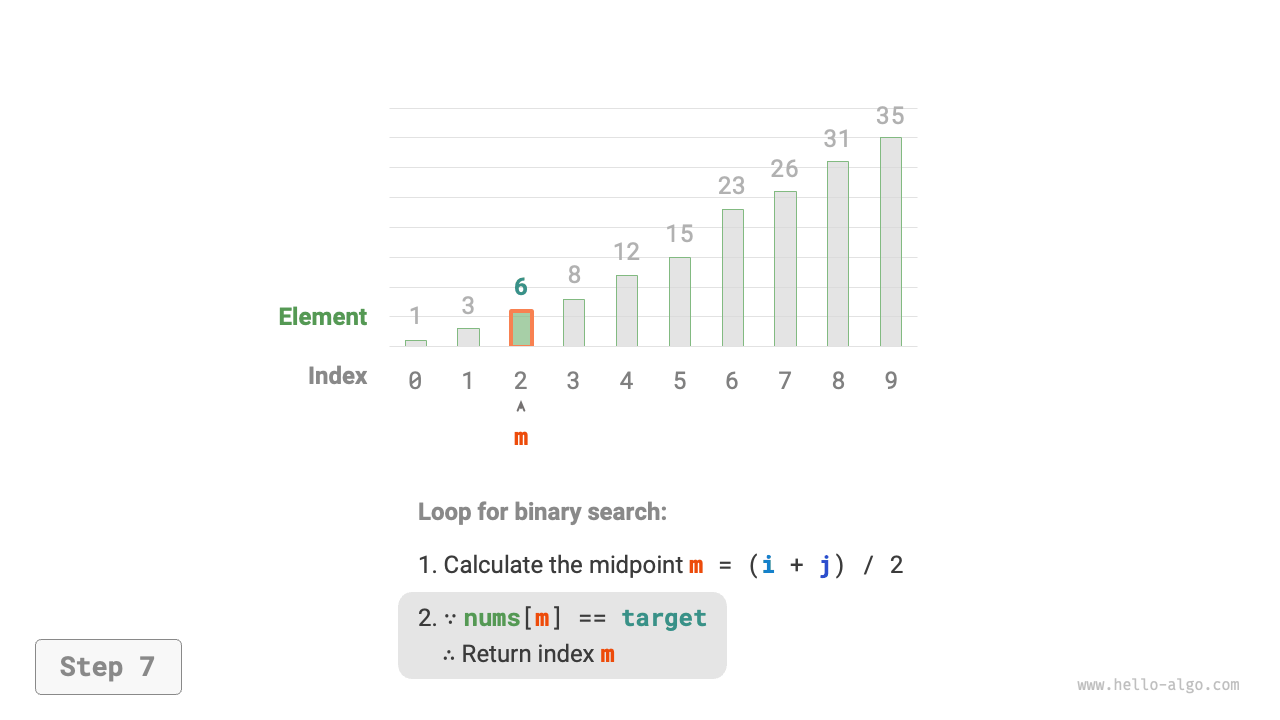
- Compare the size of
nums[m]andtarget, divided into the following three scenarios.- If
nums[m] < target, it indicates thattargetis in the interval \([m + 1, j]\), thus set \(i = m + 1\). - If
nums[m] > target, it indicates thattargetis in the interval \([i, m - 1]\), thus set \(j = m - 1\). - If
nums[m] = target, it indicates thattargetis found, thus return index \(m\).
- If
If the array does not contain the target element, the search interval will eventually reduce to empty. In this case, return \(-1\).
Figure 10-2 Binary search process
It's worth noting that since \(i\) and \(j\) are both of type int, \(i + j\) might exceed the range of int type. To avoid large number overflow, we usually use the formula \(m = \lfloor {i + (j - i) / 2} \rfloor\) to calculate the midpoint.
The code is as follows:
def binary_search(nums: list[int], target: int) -> int:
"""Binary search (double closed interval)"""
# Initialize double closed interval [0, n-1], i.e., i, j point to the first element and last element of the array respectively
i, j = 0, len(nums) - 1
# Loop until the search interval is empty (when i > j, it is empty)
while i <= j:
# Theoretically, Python's numbers can be infinitely large (depending on memory size), so there is no need to consider large number overflow
m = (i + j) // 2 # Calculate midpoint index m
if nums[m] < target:
i = m + 1 # This situation indicates that target is in the interval [m+1, j]
elif nums[m] > target:
j = m - 1 # This situation indicates that target is in the interval [i, m-1]
else:
return m # Found the target element, thus return its index
return -1 # Did not find the target element, thus return -1
/* Binary search (double closed interval) */
int binarySearch(int[] nums, int target) {
// Initialize double closed interval [0, n-1], i.e., i, j point to the first element and last element of the array respectively
int i = 0, j = nums.length - 1;
// Loop until the search interval is empty (when i > j, it is empty)
while (i <= j) {
int m = i + (j - i) / 2; // Calculate midpoint index m
if (nums[m] < target) // This situation indicates that target is in the interval [m+1, j]
i = m + 1;
else if (nums[m] > target) // This situation indicates that target is in the interval [i, m-1]
j = m - 1;
else // Found the target element, thus return its index
return m;
}
// Did not find the target element, thus return -1
return -1;
}
Time complexity is \(O(\log n)\) : In the binary loop, the interval reduces by half each round, hence the number of iterations is \(\log_2 n\).
Space complexity is \(O(1)\) : Pointers \(i\) and \(j\) use constant size space.
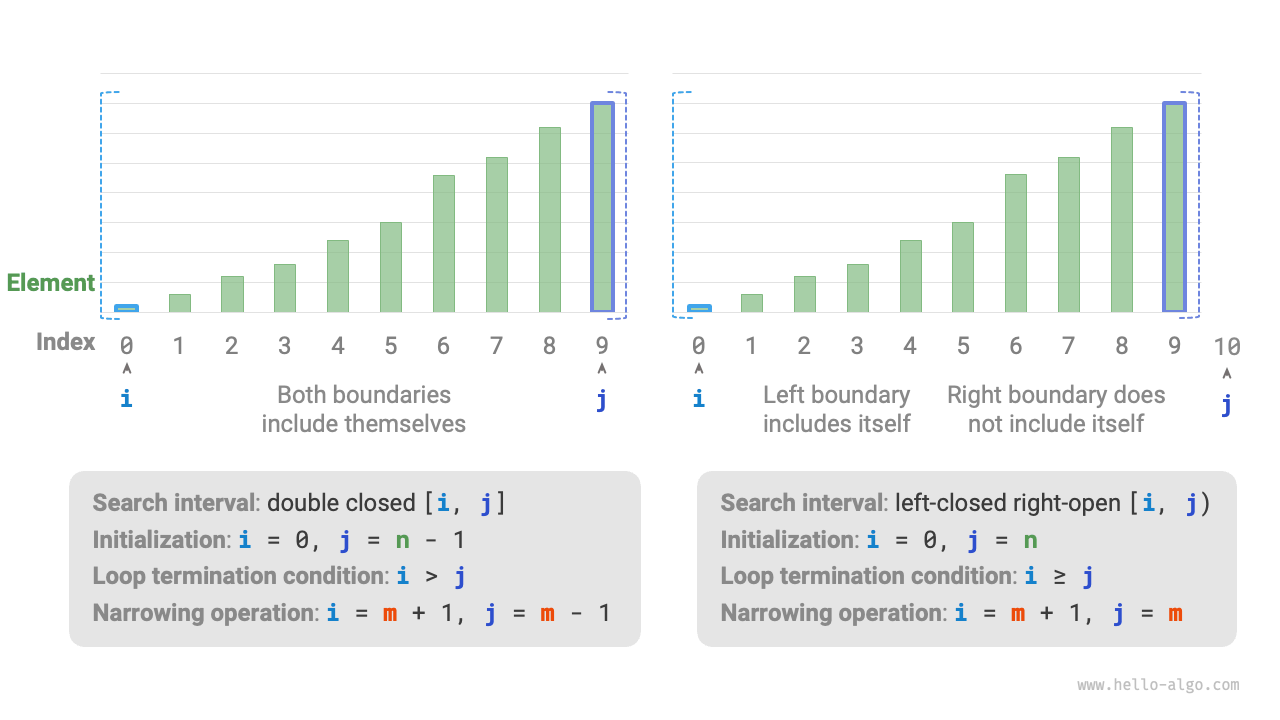
10.1.1 Interval representation methods¶
Besides the aforementioned closed interval, a common interval representation is the "left-closed right-open" interval, defined as \([0, n)\), where the left boundary includes itself, and the right boundary does not include itself. In this representation, the interval \([i, j)\) is empty when \(i = j\).
We can implement a binary search algorithm with the same functionality based on this representation:
def binary_search_lcro(nums: list[int], target: int) -> int:
"""Binary search (left closed right open interval)"""
# Initialize left closed right open interval [0, n), i.e., i, j point to the first element and the last element +1 of the array respectively
i, j = 0, len(nums)
# Loop until the search interval is empty (when i = j, it is empty)
while i < j:
m = (i + j) // 2 # Calculate midpoint index m
if nums[m] < target:
i = m + 1 # This situation indicates that target is in the interval [m+1, j)
elif nums[m] > target:
j = m # This situation indicates that target is in the interval [i, m)
else:
return m # Found the target element, thus return its index
return -1 # Did not find the target element, thus return -1
/* Binary search (left closed right open interval) */
int binarySearchLCRO(int[] nums, int target) {
// Initialize left closed right open interval [0, n), i.e., i, j point to the first element and the last element +1 of the array respectively
int i = 0, j = nums.length;
// Loop until the search interval is empty (when i = j, it is empty)
while (i < j) {
int m = i + (j - i) / 2; // Calculate midpoint index m
if (nums[m] < target) // This situation indicates that target is in the interval [m+1, j)
i = m + 1;
else if (nums[m] > target) // This situation indicates that target is in the interval [i, m)
j = m;
else // Found the target element, thus return its index
return m;
}
// Did not find the target element, thus return -1
return -1;
}
As shown in Figure 10-3, in the two types of interval representations, the initialization of the binary search algorithm, the loop condition, and the narrowing interval operation are different.
Since both boundaries in the "closed interval" representation are defined as closed, the operations to narrow the interval through pointers \(i\) and \(j\) are also symmetrical. This makes it less prone to errors, therefore, it is generally recommended to use the "closed interval" approach.
Figure 10-3 Two types of interval definitions
10.1.2 Advantages and limitations¶
Binary search performs well in both time and space aspects.
- Binary search is time-efficient. With large data volumes, the logarithmic time complexity has a significant advantage. For instance, when the data size \(n = 2^{20}\), linear search requires \(2^{20} = 1048576\) iterations, while binary search only requires \(\log_2 2^{20} = 20\) iterations.
- Binary search does not require extra space. Compared to search algorithms that rely on additional space (like hash search), binary search is more space-efficient.
However, binary search is not suitable for all situations, mainly for the following reasons.
- Binary search is only applicable to ordered data. If the input data is unordered, it is not worth sorting it just to use binary search, as sorting algorithms typically have a time complexity of \(O(n \log n)\), which is higher than both linear and binary search. For scenarios with frequent element insertion to maintain array order, inserting elements into specific positions has a time complexity of \(O(n)\), which is also quite costly.
- Binary search is only applicable to arrays. Binary search requires non-continuous (jumping) element access, which is inefficient in linked lists, thus not suitable for use in linked lists or data structures based on linked lists.
- With small data volumes, linear search performs better. In linear search, each round only requires 1 decision operation; whereas in binary search, it involves 1 addition, 1 division, 1 to 3 decision operations, 1 addition (subtraction), totaling 4 to 6 operations; therefore, when data volume \(n\) is small, linear search can be faster than binary search.