9.2 Basic operations on graphs¶
The basic operations on graphs can be divided into operations on "edges" and operations on "vertices". Under the two representation methods of "adjacency matrix" and "adjacency list", the implementation methods are different.
9.2.1 Implementation based on adjacency matrix¶
Given an undirected graph with \(n\) vertices, the various operations are implemented as shown in Figure 9-7.
- Adding or removing an edge: Directly modify the specified edge in the adjacency matrix, using \(O(1)\) time. Since it is an undirected graph, it is necessary to update the edges in both directions simultaneously.
- Adding a vertex: Add a row and a column at the end of the adjacency matrix and fill them all with \(0\)s, using \(O(n)\) time.
- Removing a vertex: Delete a row and a column in the adjacency matrix. The worst case is when the first row and column are removed, requiring \((n-1)^2\) elements to be "moved up and to the left", thus using \(O(n^2)\) time.
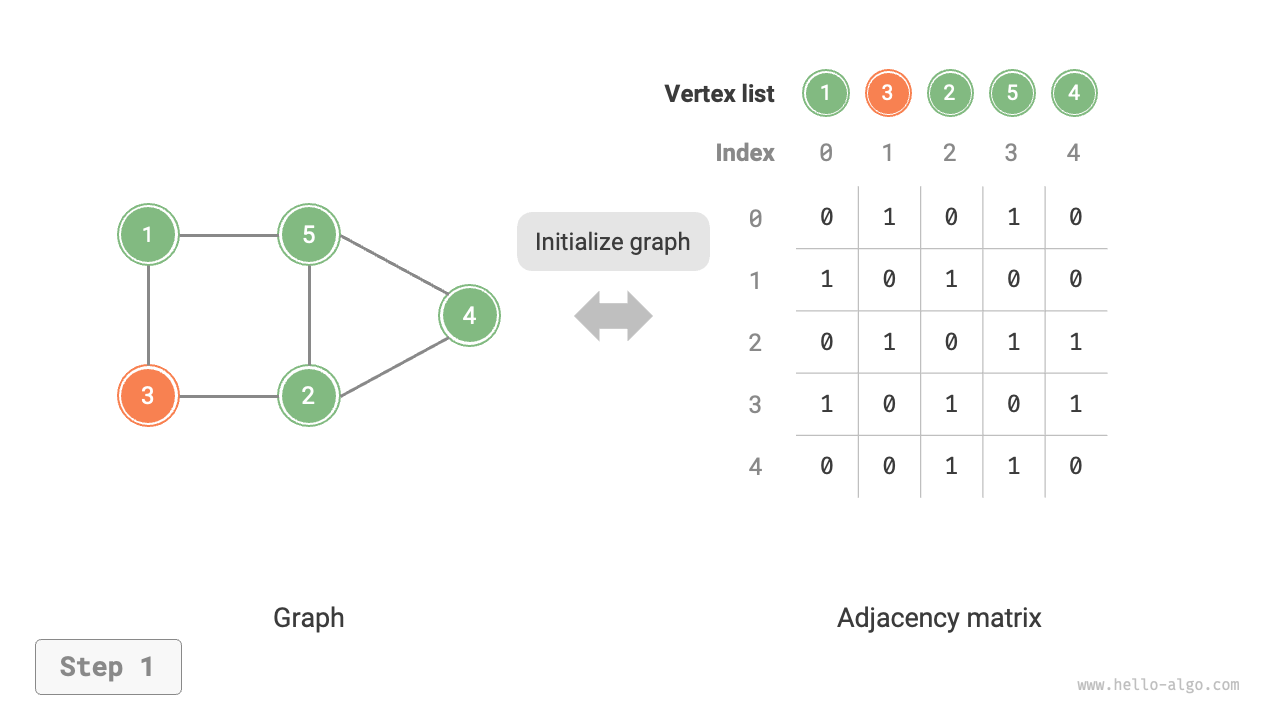
- Initialization: Pass in \(n\) vertices, initialize a vertex list
verticesof length \(n\), using \(O(n)\) time; initialize an \(n \times n\) size adjacency matrixadjMat, using \(O(n^2)\) time.
Figure 9-7 Initialization, adding and removing edges, adding and removing vertices in adjacency matrix
Below is the implementation code for graphs represented using an adjacency matrix:
class GraphAdjMat:
"""Undirected graph class based on adjacency matrix"""
def __init__(self, vertices: list[int], edges: list[list[int]]):
"""Constructor"""
# Vertex list, elements represent "vertex value", index represents "vertex index"
self.vertices: list[int] = []
# Adjacency matrix, row and column indices correspond to "vertex index"
self.adj_mat: list[list[int]] = []
# Add vertex
for val in vertices:
self.add_vertex(val)
# Add edge
# Edges elements represent vertex indices
for e in edges:
self.add_edge(e[0], e[1])
def size(self) -> int:
"""Get the number of vertices"""
return len(self.vertices)
def add_vertex(self, val: int):
"""Add vertex"""
n = self.size()
# Add new vertex value to the vertex list
self.vertices.append(val)
# Add a row to the adjacency matrix
new_row = [0] * n
self.adj_mat.append(new_row)
# Add a column to the adjacency matrix
for row in self.adj_mat:
row.append(0)
def remove_vertex(self, index: int):
"""Remove vertex"""
if index >= self.size():
raise IndexError()
# Remove vertex at `index` from the vertex list
self.vertices.pop(index)
# Remove the row at `index` from the adjacency matrix
self.adj_mat.pop(index)
# Remove the column at `index` from the adjacency matrix
for row in self.adj_mat:
row.pop(index)
def add_edge(self, i: int, j: int):
"""Add edge"""
# Parameters i, j correspond to vertices element indices
# Handle index out of bounds and equality
if i < 0 or j < 0 or i >= self.size() or j >= self.size() or i == j:
raise IndexError()
# In an undirected graph, the adjacency matrix is symmetric about the main diagonal, i.e., satisfies (i, j) == (j, i)
self.adj_mat[i][j] = 1
self.adj_mat[j][i] = 1
def remove_edge(self, i: int, j: int):
"""Remove edge"""
# Parameters i, j correspond to vertices element indices
# Handle index out of bounds and equality
if i < 0 or j < 0 or i >= self.size() or j >= self.size() or i == j:
raise IndexError()
self.adj_mat[i][j] = 0
self.adj_mat[j][i] = 0
def print(self):
"""Print adjacency matrix"""
print("Vertex list =", self.vertices)
print("Adjacency matrix =")
print_matrix(self.adj_mat)
/* Undirected graph class based on adjacency matrix */
class GraphAdjMat {
vector<int> vertices; // Vertex list, elements represent "vertex value", index represents "vertex index"
vector<vector<int>> adjMat; // Adjacency matrix, row and column indices correspond to "vertex index"
public:
/* Constructor */
GraphAdjMat(const vector<int> &vertices, const vector<vector<int>> &edges) {
// Add vertex
for (int val : vertices) {
addVertex(val);
}
// Add edge
// Edges elements represent vertex indices
for (const vector<int> &edge : edges) {
addEdge(edge[0], edge[1]);
}
}
/* Get the number of vertices */
int size() const {
return vertices.size();
}
/* Add vertex */
void addVertex(int val) {
int n = size();
// Add new vertex value to the vertex list
vertices.push_back(val);
// Add a row to the adjacency matrix
adjMat.emplace_back(vector<int>(n, 0));
// Add a column to the adjacency matrix
for (vector<int> &row : adjMat) {
row.push_back(0);
}
}
/* Remove vertex */
void removeVertex(int index) {
if (index >= size()) {
throw out_of_range("Vertex does not exist");
}
// Remove vertex at `index` from the vertex list
vertices.erase(vertices.begin() + index);
// Remove the row at `index` from the adjacency matrix
adjMat.erase(adjMat.begin() + index);
// Remove the column at `index` from the adjacency matrix
for (vector<int> &row : adjMat) {
row.erase(row.begin() + index);
}
}
/* Add edge */
// Parameters i, j correspond to vertices element indices
void addEdge(int i, int j) {
// Handle index out of bounds and equality
if (i < 0 || j < 0 || i >= size() || j >= size() || i == j) {
throw out_of_range("Vertex does not exist");
}
// In an undirected graph, the adjacency matrix is symmetric about the main diagonal, i.e., satisfies (i, j) == (j, i)
adjMat[i][j] = 1;
adjMat[j][i] = 1;
}
/* Remove edge */
// Parameters i, j correspond to vertices element indices
void removeEdge(int i, int j) {
// Handle index out of bounds and equality
if (i < 0 || j < 0 || i >= size() || j >= size() || i == j) {
throw out_of_range("Vertex does not exist");
}
adjMat[i][j] = 0;
adjMat[j][i] = 0;
}
/* Print adjacency matrix */
void print() {
cout << "Vertex list = ";
printVector(vertices);
cout << "Adjacency matrix =" << endl;
printVectorMatrix(adjMat);
}
};
/* Undirected graph class based on adjacency matrix */
class GraphAdjMat {
List<Integer> vertices; // Vertex list, elements represent "vertex value", index represents "vertex index"
List<List<Integer>> adjMat; // Adjacency matrix, row and column indices correspond to "vertex index"
/* Constructor */
public GraphAdjMat(int[] vertices, int[][] edges) {
this.vertices = new ArrayList<>();
this.adjMat = new ArrayList<>();
// Add vertex
for (int val : vertices) {
addVertex(val);
}
// Add edge
// Edges elements represent vertex indices
for (int[] e : edges) {
addEdge(e[0], e[1]);
}
}
/* Get the number of vertices */
public int size() {
return vertices.size();
}
/* Add vertex */
public void addVertex(int val) {
int n = size();
// Add new vertex value to the vertex list
vertices.add(val);
// Add a row to the adjacency matrix
List<Integer> newRow = new ArrayList<>(n);
for (int j = 0; j < n; j++) {
newRow.add(0);
}
adjMat.add(newRow);
// Add a column to the adjacency matrix
for (List<Integer> row : adjMat) {
row.add(0);
}
}
/* Remove vertex */
public void removeVertex(int index) {
if (index >= size())
throw new IndexOutOfBoundsException();
// Remove vertex at `index` from the vertex list
vertices.remove(index);
// Remove the row at `index` from the adjacency matrix
adjMat.remove(index);
// Remove the column at `index` from the adjacency matrix
for (List<Integer> row : adjMat) {
row.remove(index);
}
}
/* Add edge */
// Parameters i, j correspond to vertices element indices
public void addEdge(int i, int j) {
// Handle index out of bounds and equality
if (i < 0 || j < 0 || i >= size() || j >= size() || i == j)
throw new IndexOutOfBoundsException();
// In an undirected graph, the adjacency matrix is symmetric about the main diagonal, i.e., satisfies (i, j) == (j, i)
adjMat.get(i).set(j, 1);
adjMat.get(j).set(i, 1);
}
/* Remove edge */
// Parameters i, j correspond to vertices element indices
public void removeEdge(int i, int j) {
// Handle index out of bounds and equality
if (i < 0 || j < 0 || i >= size() || j >= size() || i == j)
throw new IndexOutOfBoundsException();
adjMat.get(i).set(j, 0);
adjMat.get(j).set(i, 0);
}
/* Print adjacency matrix */
public void print() {
System.out.print("Vertex list = ");
System.out.println(vertices);
System.out.println("Adjacency matrix =");
PrintUtil.printMatrix(adjMat);
}
}
9.2.2 Implementation based on adjacency list¶
Given an undirected graph with a total of \(n\) vertices and \(m\) edges, the various operations can be implemented as shown in Figure 9-8.
- Adding an edge: Simply add the edge at the end of the corresponding vertex's linked list, using \(O(1)\) time. Because it is an undirected graph, it is necessary to add edges in both directions simultaneously.
- Removing an edge: Find and remove the specified edge in the corresponding vertex's linked list, using \(O(m)\) time. In an undirected graph, it is necessary to remove edges in both directions simultaneously.
- Adding a vertex: Add a linked list in the adjacency list and make the new vertex the head node of the list, using \(O(1)\) time.
- Removing a vertex: It is necessary to traverse the entire adjacency list, removing all edges that include the specified vertex, using \(O(n + m)\) time.
- Initialization: Create \(n\) vertices and \(2m\) edges in the adjacency list, using \(O(n + m)\) time.
Figure 9-8 Initialization, adding and removing edges, adding and removing vertices in adjacency list
Below is the adjacency list code implementation. Compared to Figure 9-8, the actual code has the following differences.
- For convenience in adding and removing vertices, and to simplify the code, we use lists (dynamic arrays) instead of linked lists.
- Use a hash table to store the adjacency list,
keybeing the vertex instance,valuebeing the list (linked list) of adjacent vertices of that vertex.
Additionally, we use the Vertex class to represent vertices in the adjacency list. The reason for this is: if, like with the adjacency matrix, list indexes were used to distinguish different vertices, then suppose you want to delete the vertex at index \(i\), you would need to traverse the entire adjacency list and decrement all indexes greater than \(i\) by \(1\), which is very inefficient. However, if each vertex is a unique Vertex instance, then deleting a vertex does not require any changes to other vertices.
class GraphAdjList:
"""Undirected graph class based on adjacency list"""
def __init__(self, edges: list[list[Vertex]]):
"""Constructor"""
# Adjacency list, key: vertex, value: all adjacent vertices of that vertex
self.adj_list = dict[Vertex, list[Vertex]]()
# Add all vertices and edges
for edge in edges:
self.add_vertex(edge[0])
self.add_vertex(edge[1])
self.add_edge(edge[0], edge[1])
def size(self) -> int:
"""Get the number of vertices"""
return len(self.adj_list)
def add_edge(self, vet1: Vertex, vet2: Vertex):
"""Add edge"""
if vet1 not in self.adj_list or vet2 not in self.adj_list or vet1 == vet2:
raise ValueError()
# Add edge vet1 - vet2
self.adj_list[vet1].append(vet2)
self.adj_list[vet2].append(vet1)
def remove_edge(self, vet1: Vertex, vet2: Vertex):
"""Remove edge"""
if vet1 not in self.adj_list or vet2 not in self.adj_list or vet1 == vet2:
raise ValueError()
# Remove edge vet1 - vet2
self.adj_list[vet1].remove(vet2)
self.adj_list[vet2].remove(vet1)
def add_vertex(self, vet: Vertex):
"""Add vertex"""
if vet in self.adj_list:
return
# Add a new linked list to the adjacency list
self.adj_list[vet] = []
def remove_vertex(self, vet: Vertex):
"""Remove vertex"""
if vet not in self.adj_list:
raise ValueError()
# Remove the vertex vet's corresponding linked list from the adjacency list
self.adj_list.pop(vet)
# Traverse other vertices' linked lists, removing all edges containing vet
for vertex in self.adj_list:
if vet in self.adj_list[vertex]:
self.adj_list[vertex].remove(vet)
def print(self):
"""Print the adjacency list"""
print("Adjacency list =")
for vertex in self.adj_list:
tmp = [v.val for v in self.adj_list[vertex]]
print(f"{vertex.val}: {tmp},")
/* Undirected graph class based on adjacency list */
class GraphAdjList {
public:
// Adjacency list, key: vertex, value: all adjacent vertices of that vertex
unordered_map<Vertex *, vector<Vertex *>> adjList;
/* Remove a specified node from vector */
void remove(vector<Vertex *> &vec, Vertex *vet) {
for (int i = 0; i < vec.size(); i++) {
if (vec[i] == vet) {
vec.erase(vec.begin() + i);
break;
}
}
}
/* Constructor */
GraphAdjList(const vector<vector<Vertex *>> &edges) {
// Add all vertices and edges
for (const vector<Vertex *> &edge : edges) {
addVertex(edge[0]);
addVertex(edge[1]);
addEdge(edge[0], edge[1]);
}
}
/* Get the number of vertices */
int size() {
return adjList.size();
}
/* Add edge */
void addEdge(Vertex *vet1, Vertex *vet2) {
if (!adjList.count(vet1) || !adjList.count(vet2) || vet1 == vet2)
throw invalid_argument("Vertex does not exist");
// Add edge vet1 - vet2
adjList[vet1].push_back(vet2);
adjList[vet2].push_back(vet1);
}
/* Remove edge */
void removeEdge(Vertex *vet1, Vertex *vet2) {
if (!adjList.count(vet1) || !adjList.count(vet2) || vet1 == vet2)
throw invalid_argument("Vertex does not exist");
// Remove edge vet1 - vet2
remove(adjList[vet1], vet2);
remove(adjList[vet2], vet1);
}
/* Add vertex */
void addVertex(Vertex *vet) {
if (adjList.count(vet))
return;
// Add a new linked list to the adjacency list
adjList[vet] = vector<Vertex *>();
}
/* Remove vertex */
void removeVertex(Vertex *vet) {
if (!adjList.count(vet))
throw invalid_argument("Vertex does not exist");
// Remove the vertex vet's corresponding linked list from the adjacency list
adjList.erase(vet);
// Traverse other vertices' linked lists, removing all edges containing vet
for (auto &adj : adjList) {
remove(adj.second, vet);
}
}
/* Print the adjacency list */
void print() {
cout << "Adjacency list =" << endl;
for (auto &adj : adjList) {
const auto &key = adj.first;
const auto &vec = adj.second;
cout << key->val << ": ";
printVector(vetsToVals(vec));
}
}
};
/* Undirected graph class based on adjacency list */
class GraphAdjList {
// Adjacency list, key: vertex, value: all adjacent vertices of that vertex
Map<Vertex, List<Vertex>> adjList;
/* Constructor */
public GraphAdjList(Vertex[][] edges) {
this.adjList = new HashMap<>();
// Add all vertices and edges
for (Vertex[] edge : edges) {
addVertex(edge[0]);
addVertex(edge[1]);
addEdge(edge[0], edge[1]);
}
}
/* Get the number of vertices */
public int size() {
return adjList.size();
}
/* Add edge */
public void addEdge(Vertex vet1, Vertex vet2) {
if (!adjList.containsKey(vet1) || !adjList.containsKey(vet2) || vet1 == vet2)
throw new IllegalArgumentException();
// Add edge vet1 - vet2
adjList.get(vet1).add(vet2);
adjList.get(vet2).add(vet1);
}
/* Remove edge */
public void removeEdge(Vertex vet1, Vertex vet2) {
if (!adjList.containsKey(vet1) || !adjList.containsKey(vet2) || vet1 == vet2)
throw new IllegalArgumentException();
// Remove edge vet1 - vet2
adjList.get(vet1).remove(vet2);
adjList.get(vet2).remove(vet1);
}
/* Add vertex */
public void addVertex(Vertex vet) {
if (adjList.containsKey(vet))
return;
// Add a new linked list to the adjacency list
adjList.put(vet, new ArrayList<>());
}
/* Remove vertex */
public void removeVertex(Vertex vet) {
if (!adjList.containsKey(vet))
throw new IllegalArgumentException();
// Remove the vertex vet's corresponding linked list from the adjacency list
adjList.remove(vet);
// Traverse other vertices' linked lists, removing all edges containing vet
for (List<Vertex> list : adjList.values()) {
list.remove(vet);
}
}
/* Print the adjacency list */
public void print() {
System.out.println("Adjacency list =");
for (Map.Entry<Vertex, List<Vertex>> pair : adjList.entrySet()) {
List<Integer> tmp = new ArrayList<>();
for (Vertex vertex : pair.getValue())
tmp.add(vertex.val);
System.out.println(pair.getKey().val + ": " + tmp + ",");
}
}
}
9.2.3 Efficiency comparison¶
Assuming there are \(n\) vertices and \(m\) edges in the graph, Table 9-2 compares the time efficiency and space efficiency of the adjacency matrix and adjacency list.
Table 9-2 Comparison of adjacency matrix and adjacency list
| Adjacency matrix | Adjacency list (Linked list) | Adjacency list (Hash table) | |
|---|---|---|---|
| Determine adjacency | \(O(1)\) | \(O(m)\) | \(O(1)\) |
| Add an edge | \(O(1)\) | \(O(1)\) | \(O(1)\) |
| Remove an edge | \(O(1)\) | \(O(m)\) | \(O(1)\) |
| Add a vertex | \(O(n)\) | \(O(1)\) | \(O(1)\) |
| Remove a vertex | \(O(n^2)\) | \(O(n + m)\) | \(O(n)\) |
| Memory space usage | \(O(n^2)\) | \(O(n + m)\) | \(O(n + m)\) |
Observing Table 9-2, it seems that the adjacency list (hash table) has the best time efficiency and space efficiency. However, in practice, operating on edges in the adjacency matrix is more efficient, requiring only a single array access or assignment operation. Overall, the adjacency matrix exemplifies the principle of "space for time", while the adjacency list exemplifies "time for space".