15.3   最大容量問題

Question

輸入一個陣列 \(ht\) ，其中的每個元素代表一個垂直隔板的高度。陣列中的任意兩個隔板，以及它們之間的空間可以組成一個容器。

容器的容量等於高度和寬度的乘積（面積），其中高度由較短的隔板決定，寬度是兩個隔板的陣列索引之差。

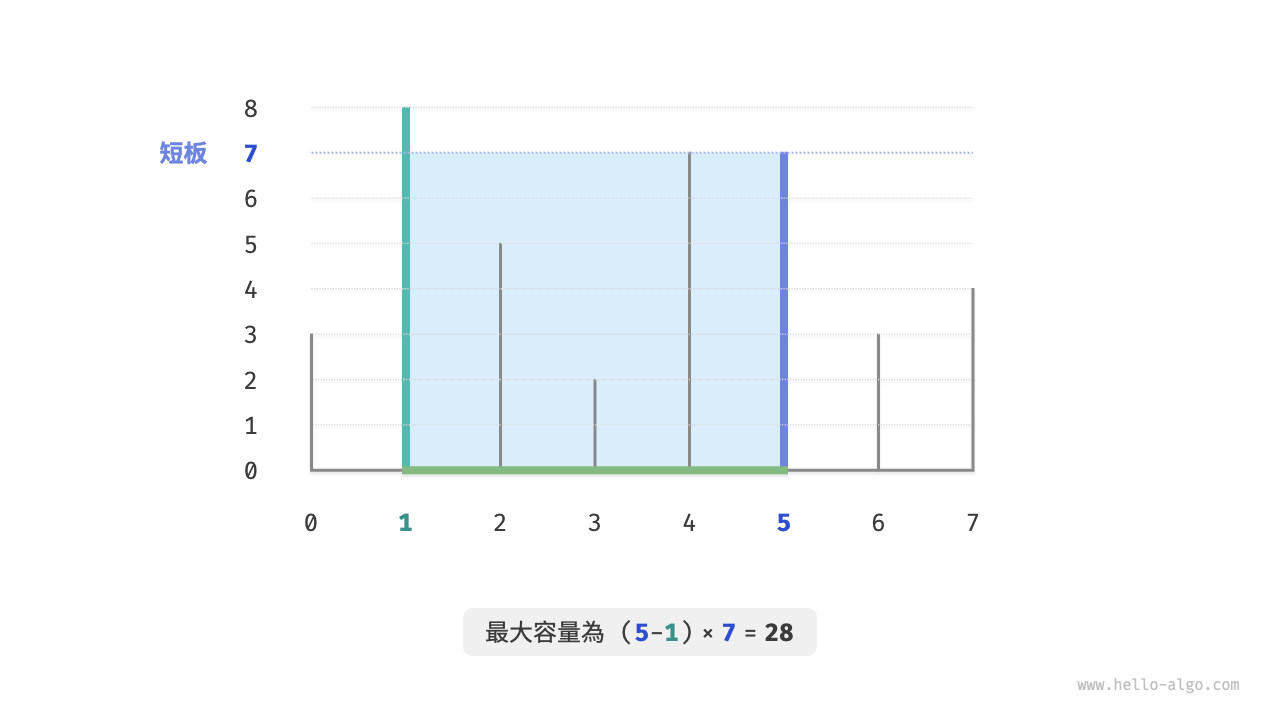
請在陣列中選擇兩個隔板，使得組成的容器的容量最大，返回最大容量。示例如圖 15-7 所示。

圖 15-7   最大容量問題的示例資料

容器由任意兩個隔板圍成，因此本題的狀態為兩個隔板的索引，記為 \([i, j]\) 。

根據題意，容量等於高度乘以寬度，其中高度由短板決定，寬度是兩隔板的陣列索引之差。設容量為 \(cap[i, j]\) ，則可得計算公式：

\[ cap[i, j] = \min(ht[i], ht[j]) \times (j - i) \]

設陣列長度為 \(n\) ，兩個隔板的組合數量（狀態總數）為 \(C_n^2 = \frac{n(n - 1)}{2}\) 個。最直接地，我們可以窮舉所有狀態，從而求得最大容量，時間複雜度為 \(O(n^2)\) 。

1.   貪婪策略確定

這道題還有更高效率的解法。如圖 15-8 所示，現選取一個狀態 \([i, j]\) ，其滿足索引 \(i < j\) 且高度 \(ht[i] < ht[j]\) ，即 \(i\) 為短板、\(j\) 為長板。

圖 15-8   初始狀態

如圖 15-9 所示，若此時將長板 \(j\) 向短板 \(i\) 靠近，則容量一定變小。

這是因為在移動長板 \(j\) 後，寬度 \(j-i\) 肯定變小；而高度由短板決定，因此高度只可能不變（ \(i\) 仍為短板）或變小（移動後的 \(j\) 成為短板）。

圖 15-9   向內移動長板後的狀態

反向思考，我們只有向內收縮短板 \(i\) ，才有可能使容量變大。因為雖然寬度一定變小，但高度可能會變大（移動後的短板 \(i\) 可能會變長）。例如在圖 15-10 中，移動短板後面積變大。

圖 15-10   向內移動短板後的狀態

由此便可推出本題的貪婪策略：初始化兩指標，使其分列容器兩端，每輪向內收縮短板對應的指標，直至兩指標相遇。

圖 15-11 展示了貪婪策略的執行過程。

1. 初始狀態下，指標 \(i\) 和 \(j\) 分列陣列兩端。
2. 計算當前狀態的容量 \(cap[i, j]\) ，並更新最大容量。
3. 比較板 \(i\) 和 板 \(j\) 的高度，並將短板向內移動一格。
4. 迴圈執行第 2. 步和第 3. 步，直至 \(i\) 和 \(j\) 相遇時結束。

<1><2><3><4><5><6><7><8><9>

圖 15-11   最大容量問題的貪婪過程

2.   程式碼實現

程式碼迴圈最多 \(n\) 輪，因此時間複雜度為 \(O(n)\) 。

變數 \(i\)、\(j\)、\(res\) 使用常數大小的額外空間，因此空間複雜度為 \(O(1)\) 。

PythonC++JavaC#GoSwiftJSTSDartRustCKotlinRubyZig

max_capacity.py

def max_capacity(ht: list[int]) -> int:
    """最大容量：貪婪"""
    # 初始化 i, j，使其分列陣列兩端
    i, j = 0, len(ht) - 1
    # 初始最大容量為 0
    res = 0
    # 迴圈貪婪選擇，直至兩板相遇
    while i < j:
        # 更新最大容量
        cap = min(ht[i], ht[j]) * (j - i)
        res = max(res, cap)
        # 向內移動短板
        if ht[i] < ht[j]:
            i += 1
        else:
            j -= 1
    return res

max_capacity.cpp

/* 最大容量：貪婪 */
int maxCapacity(vector<int> &ht) {
    // 初始化 i, j，使其分列陣列兩端
    int i = 0, j = ht.size() - 1;
    // 初始最大容量為 0
    int res = 0;
    // 迴圈貪婪選擇，直至兩板相遇
    while (i < j) {
        // 更新最大容量
        int cap = min(ht[i], ht[j]) * (j - i);
        res = max(res, cap);
        // 向內移動短板
        if (ht[i] < ht[j]) {
            i++;
        } else {
            j--;
        }
    }
    return res;
}

max_capacity.java

/* 最大容量：貪婪 */
int maxCapacity(int[] ht) {
    // 初始化 i, j，使其分列陣列兩端
    int i = 0, j = ht.length - 1;
    // 初始最大容量為 0
    int res = 0;
    // 迴圈貪婪選擇，直至兩板相遇
    while (i < j) {
        // 更新最大容量
        int cap = Math.min(ht[i], ht[j]) * (j - i);
        res = Math.max(res, cap);
        // 向內移動短板
        if (ht[i] < ht[j]) {
            i++;
        } else {
            j--;
        }
    }
    return res;
}

max_capacity.cs

/* 最大容量：貪婪 */
int MaxCapacity(int[] ht) {
    // 初始化 i, j，使其分列陣列兩端
    int i = 0, j = ht.Length - 1;
    // 初始最大容量為 0
    int res = 0;
    // 迴圈貪婪選擇，直至兩板相遇
    while (i < j) {
        // 更新最大容量
        int cap = Math.Min(ht[i], ht[j]) * (j - i);
        res = Math.Max(res, cap);
        // 向內移動短板
        if (ht[i] < ht[j]) {
            i++;
        } else {
            j--;
        }
    }
    return res;
}

max_capacity.go

/* 最大容量：貪婪 */
func maxCapacity(ht []int) int {
    // 初始化 i, j，使其分列陣列兩端
    i, j := 0, len(ht)-1
    // 初始最大容量為 0
    res := 0
    // 迴圈貪婪選擇，直至兩板相遇
    for i < j {
        // 更新最大容量
        capacity := int(math.Min(float64(ht[i]), float64(ht[j]))) * (j - i)
        res = int(math.Max(float64(res), float64(capacity)))
        // 向內移動短板
        if ht[i] < ht[j] {
            i++
        } else {
            j--
        }
    }
    return res
}

max_capacity.swift

/* 最大容量：貪婪 */
func maxCapacity(ht: [Int]) -> Int {
    // 初始化 i, j，使其分列陣列兩端
    var i = ht.startIndex, j = ht.endIndex - 1
    // 初始最大容量為 0
    var res = 0
    // 迴圈貪婪選擇，直至兩板相遇
    while i < j {
        // 更新最大容量
        let cap = min(ht[i], ht[j]) * (j - i)
        res = max(res, cap)
        // 向內移動短板
        if ht[i] < ht[j] {
            i += 1
        } else {
            j -= 1
        }
    }
    return res
}

max_capacity.js

/* 最大容量：貪婪 */
function maxCapacity(ht) {
    // 初始化 i, j，使其分列陣列兩端
    let i = 0,
        j = ht.length - 1;
    // 初始最大容量為 0
    let res = 0;
    // 迴圈貪婪選擇，直至兩板相遇
    while (i < j) {
        // 更新最大容量
        const cap = Math.min(ht[i], ht[j]) * (j - i);
        res = Math.max(res, cap);
        // 向內移動短板
        if (ht[i] < ht[j]) {
            i += 1;
        } else {
            j -= 1;
        }
    }
    return res;
}

max_capacity.ts

/* 最大容量：貪婪 */
function maxCapacity(ht: number[]): number {
    // 初始化 i, j，使其分列陣列兩端
    let i = 0,
        j = ht.length - 1;
    // 初始最大容量為 0
    let res = 0;
    // 迴圈貪婪選擇，直至兩板相遇
    while (i < j) {
        // 更新最大容量
        const cap: number = Math.min(ht[i], ht[j]) * (j - i);
        res = Math.max(res, cap);
        // 向內移動短板
        if (ht[i] < ht[j]) {
            i += 1;
        } else {
            j -= 1;
        }
    }
    return res;
}

max_capacity.dart

/* 最大容量：貪婪 */
int maxCapacity(List<int> ht) {
  // 初始化 i, j，使其分列陣列兩端
  int i = 0, j = ht.length - 1;
  // 初始最大容量為 0
  int res = 0;
  // 迴圈貪婪選擇，直至兩板相遇
  while (i < j) {
    // 更新最大容量
    int cap = min(ht[i], ht[j]) * (j - i);
    res = max(res, cap);
    // 向內移動短板
    if (ht[i] < ht[j]) {
      i++;
    } else {
      j--;
    }
  }
  return res;
}

max_capacity.rs

/* 最大容量：貪婪 */
fn max_capacity(ht: &[i32]) -> i32 {
    // 初始化 i, j，使其分列陣列兩端
    let mut i = 0;
    let mut j = ht.len() - 1;
    // 初始最大容量為 0
    let mut res = 0;
    // 迴圈貪婪選擇，直至兩板相遇
    while i < j {
        // 更新最大容量
        let cap = std::cmp::min(ht[i], ht[j]) * (j - i) as i32;
        res = std::cmp::max(res, cap);
        // 向內移動短板
        if ht[i] < ht[j] {
            i += 1;
        } else {
            j -= 1;
        }
    }
    res
}

max_capacity.c

/* 最大容量：貪婪 */
int maxCapacity(int ht[], int htLength) {
    // 初始化 i, j，使其分列陣列兩端
    int i = 0;
    int j = htLength - 1;
    // 初始最大容量為 0
    int res = 0;
    // 迴圈貪婪選擇，直至兩板相遇
    while (i < j) {
        // 更新最大容量
        int capacity = myMin(ht[i], ht[j]) * (j - i);
        res = myMax(res, capacity);
        // 向內移動短板
        if (ht[i] < ht[j]) {
            i++;
        } else {
            j--;
        }
    }
    return res;
}

max_capacity.kt

/* 最大容量：貪婪 */
fun maxCapacity(ht: IntArray): Int {
    // 初始化 i, j，使其分列陣列兩端
    var i = 0
    var j = ht.size - 1
    // 初始最大容量為 0
    var res = 0
    // 迴圈貪婪選擇，直至兩板相遇
    while (i < j) {
        // 更新最大容量
        val cap = min(ht[i], ht[j]) * (j - i)
        res = max(res, cap)
        // 向內移動短板
        if (ht[i] < ht[j]) {
            i++
        } else {
            j--
        }
    }
    return res
}

max_capacity.rb

### 最大容量：貪婪 ###
def max_capacity(ht)
  # 初始化 i, j，使其分列陣列兩端
  i, j = 0, ht.length - 1
  # 初始最大容量為 0
  res = 0

  # 迴圈貪婪選擇，直至兩板相遇
  while i < j
    # 更新最大容量
    cap = [ht[i], ht[j]].min * (j - i)
    res = [res, cap].max
    # 向內移動短板
    if ht[i] < ht[j]
      i += 1
    else
      j -= 1
    end
  end

  res
end

max_capacity.zig

[class]{}-[func]{maxCapacity}

視覺化執行

全螢幕觀看 >

3.   正確性證明

之所以貪婪比窮舉更快，是因為每輪的貪婪選擇都會“跳過”一些狀態。

比如在狀態 \(cap[i, j]\) 下，\(i\) 為短板、\(j\) 為長板。若貪婪地將短板 \(i\) 向內移動一格，會導致圖 15-12 所示的狀態被“跳過”。這意味著之後無法驗證這些狀態的容量大小。

\[ cap[i, i+1], cap[i, i+2], \dots, cap[i, j-2], cap[i, j-1] \]

圖 15-12   移動短板導致被跳過的狀態

觀察發現，這些被跳過的狀態實際上就是將長板 \(j\) 向內移動的所有狀態。前面我們已經證明內移長板一定會導致容量變小。也就是說，被跳過的狀態都不可能是最優解，跳過它們不會導致錯過最優解。

以上分析說明，移動短板的操作是“安全”的，貪婪策略是有效的。