10.5.   重识搜索算法

「搜索算法 Searching Algorithm」用于在数据结构（例如数组、链表、树或图）中搜索一个或一组满足特定条件的元素。

根据实现思路，搜索算法总体可分为两种：

• 通过遍历数据结构来定位目标元素，例如数组、链表、树和图的遍历等。
• 利用数据组织结构或数据包含的先验信息，实现高效元素查找，例如二分查找、哈希查找和二叉搜索树查找等。

不难发现，这些知识点都已在前面的章节中介绍过，因此搜索算法对于我们来说并不陌生。在本节中，我们将从更加系统的视角切入，重新审视搜索算法。

10.5.1.   暴力搜索

暴力搜索通过遍历数据结构的每个元素来定位目标元素。

• 「线性搜索」适用于数组和链表等线性数据结构。它从数据结构的一端开始，逐个访问元素，直到找到目标元素或到达另一端仍没有找到目标元素为止。
• 「广度优先搜索」和「深度优先搜索」是图和树的两种遍历策略。广度优先搜索从初始节点开始逐层搜索，由近及远地访问各个节点。深度优先搜索是从初始节点开始，沿着一条路径走到头为止，再回溯并尝试其他路径，直到遍历完整个数据结构。

暴力搜索的优点是简单且通用性好，无需对数据做预处理和借助额外的数据结构。

然而，此类算法的时间复杂度为 \(O(n)\) ，其中 \(n\) 为元素数量，因此在数据量较大的情况下性能较差。

10.5.2.   自适应搜索

自适应搜索利用数据的特有属性（例如有序性）来优化搜索过程，从而更高效地定位目标元素。

• 「二分查找」利用数据的有序性实现高效查找，仅适用于数组。
• 「哈希查找」利用哈希表将搜索数据和目标数据建立为键值对映射，从而实现查询操作。
• 「树查找」在特定的树结构（例如二叉搜索树）中，基于比较节点值来快速排除节点，从而定位目标元素。

此类算法的优点是效率高，时间复杂度可达到 \(O(\log n)\) 甚至 \(O(1)\) 。

然而，使用这些算法往往需要对数据进行预处理。例如，二分查找需要预先对数组进行排序，哈希查找和树查找都需要借助额外的数据结构，维护这些数据结构也需要额外的时间和空间开支。

Note

自适应搜索算法常被称为查找算法，主要关注在特定数据结构中快速检索目标元素。

10.5.3.   搜索方法选取

给定大小为 \(n\) 的一组数据，我们可以使用线性搜索、二分查找、树查找、哈希查找等多种方法在该数据中搜索目标元素。各个方法的工作原理如下图所示。

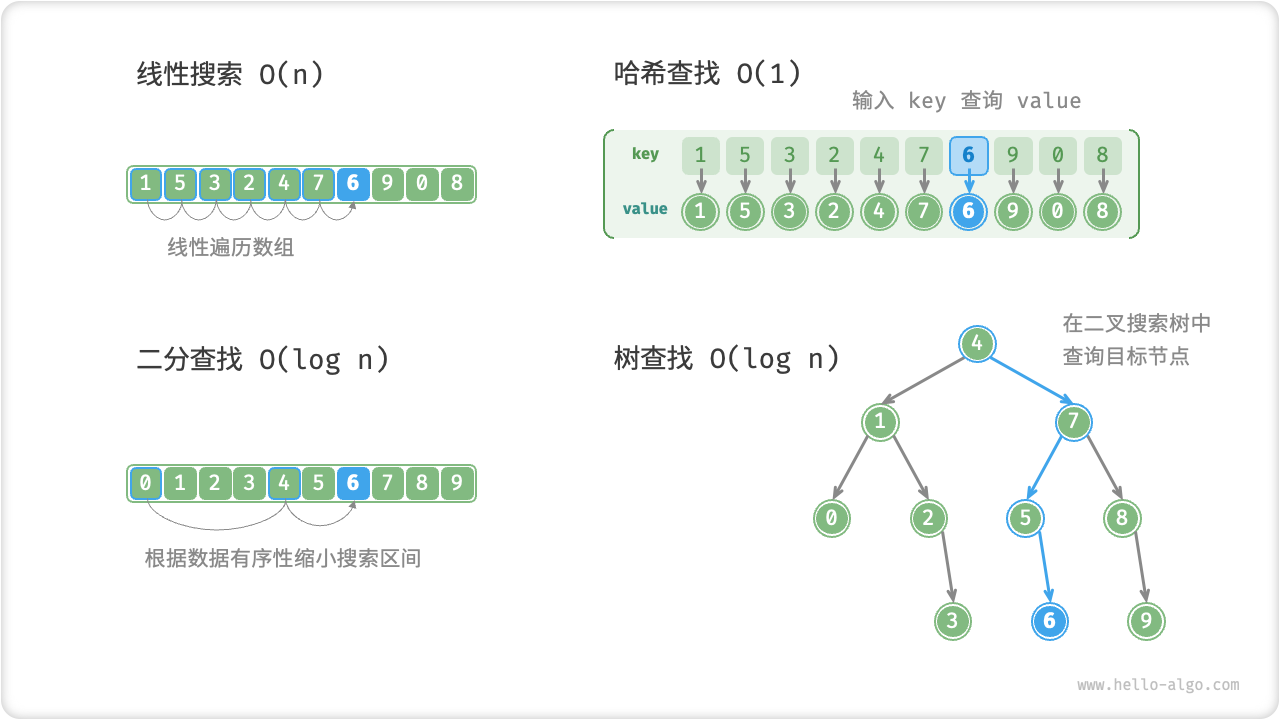
图：多种搜索策略

上述几种方法的操作效率与特性如下表所示。

	线性搜索	二分查找	树查找	哈希查找
查找元素	\(O(n)\)	\(O(\log n)\)	\(O(\log n)\)	\(O(1)\)
插入元素	\(O(1)\)	\(O(n)\)	\(O(\log n)\)	\(O(1)\)
删除元素	\(O(n)\)	\(O(n)\)	\(O(\log n)\)	\(O(1)\)
额外空间	\(O(1)\)	\(O(1)\)	\(O(n)\)	\(O(n)\)
数据预处理	/	排序 \(O(n \log n)\)	建树 \(O(n \log n)\)	建哈希表 \(O(n)\)
数据是否有序	无序	有序	有序	无序

除了以上表格内容，搜索算法的选择还取决于数据体量、搜索性能要求、数据查询与更新频率等。

线性搜索

• 通用性较好，无需任何数据预处理操作。假如我们仅需查询一次数据，那么其他三种方法的数据预处理的时间比线性搜索的时间还要更长。
• 适用于体量较小的数据，此情况下时间复杂度对效率影响较小。
• 适用于数据更新频率较高的场景，因为该方法不需要对数据进行任何额外维护。

二分查找

• 适用于大数据量的情况，效率表现稳定，最差时间复杂度为 \(O(\log n)\) 。
• 数据量不能过大，因为存储数组需要连续的内存空间。
• 不适用于高频增删数据的场景，因为维护有序数组的开销较大。

哈希查找

• 适合对查询性能要求很高的场景，平均时间复杂度为 \(O(1)\) 。
• 不适合需要有序数据或范围查找的场景，因为哈希表无法维护数据的有序性。
• 对哈希函数和哈希冲突处理策略的依赖性较高，具有较大的性能劣化风险。
• 不适合数据量过大的情况，因为哈希表需要额外空间来最大程度地减少冲突，从而提供良好的查询性能。

树查找

• 适用于海量数据，因为树节点在内存中是离散存储的。
• 适合需要维护有序数据或范围查找的场景。
• 在持续增删节点的过程中，二叉搜索树可能产生倾斜，时间复杂度劣化至 \(O(n)\) 。
• 若使用 AVL 树或红黑树，则各项操作可在 \(O(\log n)\) 效率下稳定运行，但维护树平衡的操作会增加额外开销。

评论