2.2   迭代与递归

在数据结构与算法中，重复执行某个任务是很常见的，其与算法的复杂度密切相关。而要重复执行某个任务，我们通常会选用两种基本的程序结构：迭代和递归。

2.2.1   迭代

「迭代 iteration」是一种重复执行某个任务的控制结构。在迭代中，程序会在满足一定的条件下重复执行某段代码，直到这个条件不再满足。

1.   for 循环

for 循环是最常见的迭代形式之一，适合预先知道迭代次数时使用。

以下函数基于 for 循环实现了求和 \(1 + 2 + \dots + n\) ，求和结果使用变量 res 记录。需要注意的是，Python 中 range(a, b) 对应的区间是“左闭右开”的，对应的遍历范围为 \(a, a + 1, \dots, b-1\) 。

JavaC++PythonGoJSTSCC#SwiftZigDartRust

iteration.java

/* for 循环 */
int forLoop(int n) {
    int res = 0;
    // 循环求和 1, 2, ..., n-1, n
    for (int i = 1; i <= n; i++) {
        res += i;
    }
    return res;
}

iteration.cpp

/* for 循环 */
int forLoop(int n) {
    int res = 0;
    // 循环求和 1, 2, ..., n-1, n
    for (int i = 1; i <= n; ++i) {
        res += i;
    }
    return res;
}

iteration.py

def for_loop(n: int) -> int:
    """for 循环"""
    res = 0
    # 循环求和 1, 2, ..., n-1, n
    for i in range(1, n + 1):
        res += i
    return res

iteration.go

[class]{}-[func]{forLoop}

iteration.js

[class]{}-[func]{forLoop}

iteration.ts

[class]{}-[func]{forLoop}

iteration.c

[class]{}-[func]{forLoop}

iteration.cs

[class]{iteration}-[func]{forLoop}

iteration.swift

[class]{}-[func]{forLoop}

iteration.zig

[class]{}-[func]{forLoop}

iteration.dart

/* for 循环 */
int forLoop(int n) {
  int res = 0;
  // 循环求和 1, 2, ..., n-1, n
  for (int i = 1; i <= n; i++) {
    res += i;
  }
  return res;
}

iteration.rs

[class]{}-[func]{for_loop}

图 2-1 展示了该求和函数的流程框图。

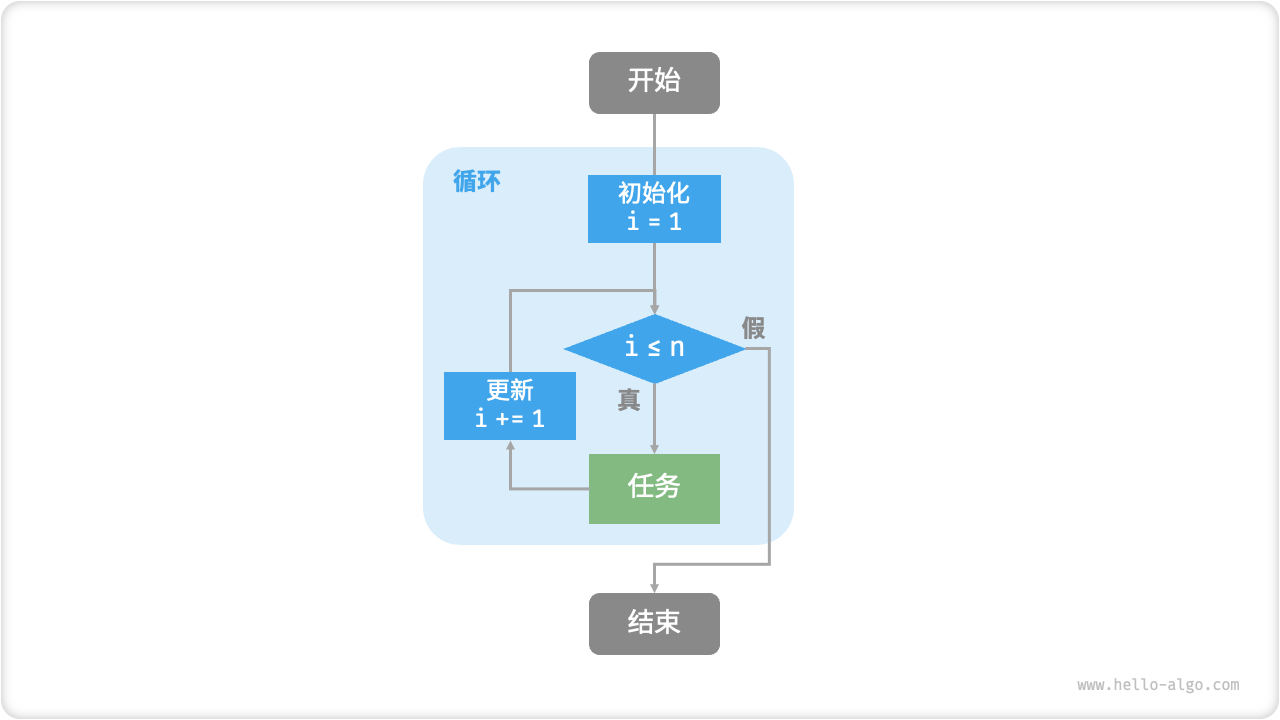
图 2-1   求和函数的流程框图

此求和函数的操作数量与输入数据大小 \(n\) 成正比，或者说成“线性关系”。实际上，时间复杂度描述的就是这个“线性关系”。相关内容将会在下一节中详细介绍。

2.   while 循环

与 for 循环类似，while 循环也是一种实现迭代的方法。在 while 循环中，程序每轮都会先检查条件，如果条件为真则继续执行，否则就结束循环。

下面，我们用 while 循环来实现求和 \(1 + 2 + \dots + n\) 。

JavaC++PythonGoJSTSCC#SwiftZigDartRust

iteration.java

/* while 循环 */
int whileLoop(int n) {
    int res = 0;
    int i = 1; // 初始化条件变量
    // 循环求和 1, 2, ..., n-1, n
    while (i <= n) {
        res += i;
        i++; // 更新条件变量
    }
    return res;
}

iteration.cpp

/* while 循环 */
int whileLoop(int n) {
    int res = 0;
    int i = 1; // 初始化条件变量
    // 循环求和 1, 2, ..., n-1, n
    while (i <= n) {
        res += i;
        i++; // 更新条件变量
    }
    return res;
}

iteration.py

def while_loop(n: int) -> int:
    """while 循环"""
    res = 0
    i = 1  # 初始化条件变量
    # 循环求和 1, 2, ..., n-1, n
    while i <= n:
        res += i
        i += 1  # 更新条件变量
    return res

iteration.go

[class]{}-[func]{whileLoop}

iteration.js

[class]{}-[func]{whileLoop}

iteration.ts

[class]{}-[func]{whileLoop}

iteration.c

[class]{}-[func]{whileLoop}

iteration.cs

[class]{iteration}-[func]{whileLoop}

iteration.swift

[class]{}-[func]{whileLoop}

iteration.zig

[class]{}-[func]{whileLoop}

iteration.dart

/* while 循环 */
int whileLoop(int n) {
  int res = 0;
  int i = 1; // 初始化条件变量
  // 循环求和 1, 2, ..., n-1, n
  while (i <= n) {
    res += i;
    i++; // 更新条件变量
  }
  return res;
}

iteration.rs

[class]{}-[func]{while_loop}

在 while 循环中，由于初始化和更新条件变量的步骤是独立在循环结构之外的，因此它比 for 循环的自由度更高。

例如在以下代码中，条件变量 \(i\) 每轮进行了两次更新，这种情况就不太方便用 for 循环实现。

JavaC++PythonGoJSTSCC#SwiftZigDartRust

iteration.java

/* while 循环（两次更新） */
int whileLoopII(int n) {
    int res = 0;
    int i = 1; // 初始化条件变量
    // 循环求和 1, 4, ...
    while (i <= n) {
        res += i;
        // 更新条件变量
        i++;
        i *= 2;
    }
    return res;
}

iteration.cpp

/* while 循环（两次更新） */
int whileLoopII(int n) {
    int res = 0;
    int i = 1; // 初始化条件变量
    // 循环求和 1, 4, ...
    while (i <= n) {
        res += i;
        // 更新条件变量
        i++;
        i *= 2;
    }
    return res;
}

iteration.py

def while_loop_ii(n: int) -> int:
    """while 循环（两次更新）"""
    res = 0
    i = 1  # 初始化条件变量
    # 循环求和 1, 4, ...
    while i <= n:
        res += i
        # 更新条件变量
        i += 1
        i *= 2
    return res

iteration.go

[class]{}-[func]{whileLoopII}

iteration.js

[class]{}-[func]{whileLoopII}

iteration.ts

[class]{}-[func]{whileLoopII}

iteration.c

[class]{}-[func]{whileLoopII}

iteration.cs

[class]{iteration}-[func]{whileLoopII}

iteration.swift

[class]{}-[func]{whileLoopII}

iteration.zig

[class]{}-[func]{whileLoopII}

iteration.dart

/* while 循环（两次更新） */
int whileLoopII(int n) {
  int res = 0;
  int i = 1; // 初始化条件变量
  // 循环求和 1, 4, ...
  while (i <= n) {
    res += i;
    // 更新条件变量
    i++;
    i *= 2;
  }
  return res;
}

iteration.rs

[class]{}-[func]{while_loop_ii}

总的来说，for 循环的代码更加紧凑，while 循环更加灵活，两者都可以实现迭代结构。选择使用哪一个应该根据特定问题的需求来决定。

3.   嵌套循环

我们可以在一个循环结构内嵌套另一个循环结构，以 for 循环为例：

JavaC++PythonGoJSTSCC#SwiftZigDartRust

iteration.java

/* 双层 for 循环 */
String nestedForLoop(int n) {
    StringBuilder res = new StringBuilder();
    // 循环 i = 1, 2, ..., n-1, n
    for (int i = 1; i <= n; i++) {
        // 循环 j = 1, 2, ..., n-1, n
        for (int j = 1; j <= n; j++) {
            res.append("(" + i + ", " + j + "), ");
        }
    }
    return res.toString();
}

iteration.cpp

/* 双层 for 循环 */
string nestedForLoop(int n) {
    ostringstream res;
    // 循环 i = 1, 2, ..., n-1, n
    for (int i = 1; i <= n; ++i) {
        // 循环 j = 1, 2, ..., n-1, n
        for (int j = 1; j <= n; ++j) {
            res << "(" << i << ", " << j << "), ";
        }
    }
    return res.str();
}

iteration.py

def nested_for_loop(n: int) -> str:
    """双层 for 循环"""
    res = ""
    # 循环 i = 1, 2, ..., n-1, n
    for i in range(1, n + 1):
        # 循环 j = 1, 2, ..., n-1, n
        for j in range(1, n + 1):
            res += f"({i}, {j}), "
    return res

iteration.go

[class]{}-[func]{nestedForLoop}

iteration.js

[class]{}-[func]{nestedForLoop}

iteration.ts

[class]{}-[func]{nestedForLoop}

iteration.c

[class]{}-[func]{nestedForLoop}

iteration.cs

[class]{iteration}-[func]{nestedForLoop}

iteration.swift

[class]{}-[func]{nestedForLoop}

iteration.zig

[class]{}-[func]{nestedForLoop}

iteration.dart

/* 双层 for 循环 */
String nestedForLoop(int n) {
  String res = "";
  // 循环 i = 1, 2, ..., n-1, n
  for (int i = 1; i <= n; i++) {
    // 循环 j = 1, 2, ..., n-1, n
    for (int j = 1; j <= n; j++) {
      res += "($i, $j), ";
    }
  }
  return res;
}

iteration.rs

[class]{}-[func]{nested_for_loop}

图 2-2 给出了该嵌套循环的流程框图。

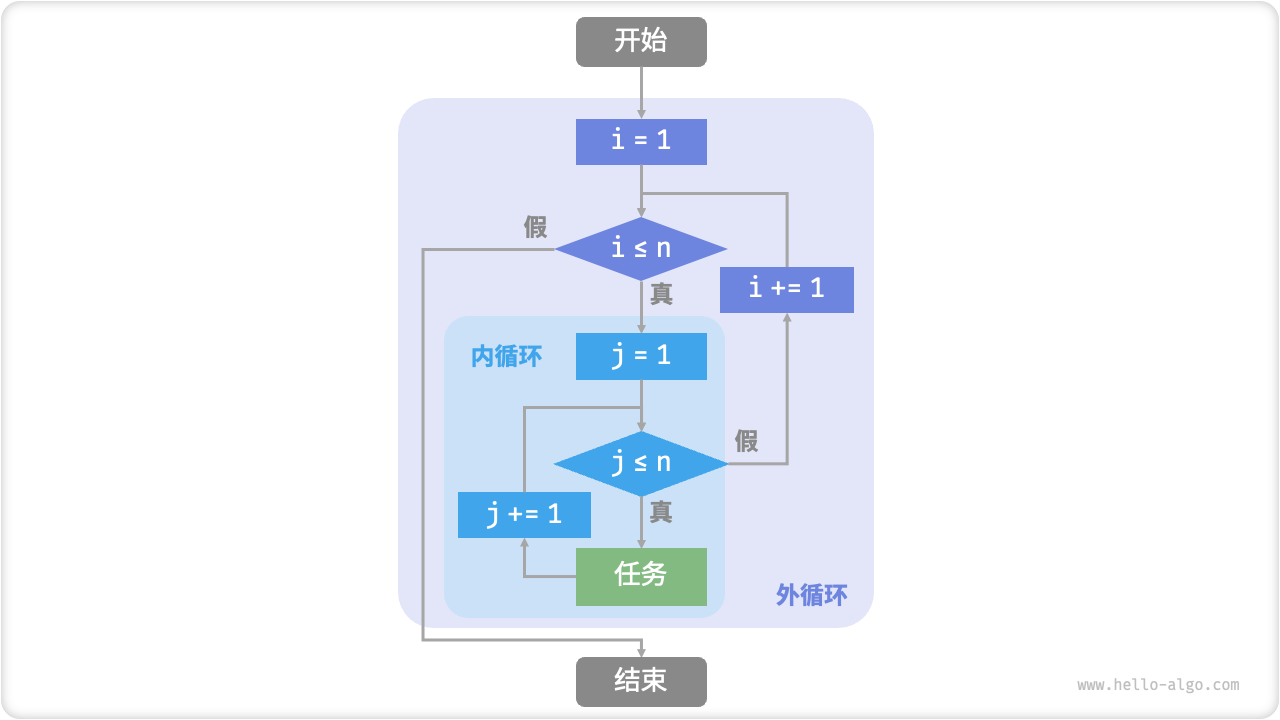
图 2-2   嵌套循环的流程框图

在这种情况下，函数的操作数量与 \(n^2\) 成正比，或者说算法运行时间和输入数据大小 \(n\) 成“平方关系”。

我们可以继续添加嵌套循环，每一次嵌套都是一次“升维”，将会使时间复杂度提高至“立方关系”、“四次方关系”、以此类推。

2.2.2   递归

「递归 recursion」是一种算法策略，通过函数调用自身来解决问题。它主要包含两个阶段。

1. 递：程序不断深入地调用自身，通常传入更小或更简化的参数，直到达到“终止条件”。
2. 归：触发“终止条件”后，程序从最深层的递归函数开始逐层返回，汇聚每一层的结果。

而从实现的角度看，递归代码主要包含三个要素。

1. 终止条件：用于决定什么时候由“递”转“归”。
2. 递归调用：对应“递”，函数调用自身，通常输入更小或更简化的参数。
3. 返回结果：对应“归”，将当前递归层级的结果返回至上一层。

观察以下代码，我们只需调用函数 recur(n) ，就可以完成 \(1 + 2 + \dots + n\) 的计算：

JavaC++PythonGoJSTSCC#SwiftZigDartRust

recursion.java

/* 递归 */
int recur(int n) {
    // 终止条件
    if (n == 1)
        return 1;
    // 递：递归调用
    int res = recur(n - 1);
    // 归：返回结果
    return n + res;
}

recursion.cpp

/* 递归 */
int recur(int n) {
    // 终止条件
    if (n == 1)
        return 1;
    // 递：递归调用
    int res = recur(n - 1);
    // 归：返回结果
    return n + res;
}

recursion.py

def recur(n: int) -> int:
    """递归"""
    # 终止条件
    if n == 1:
        return 1
    # 递：递归调用
    res = recur(n - 1)
    # 归：返回结果
    return n + res

recursion.go

[class]{}-[func]{recur}

recursion.js

[class]{}-[func]{recur}

recursion.ts

[class]{}-[func]{recur}

recursion.c

[class]{}-[func]{recur}

recursion.cs

[class]{recursion}-[func]{recur}

recursion.swift

[class]{}-[func]{recur}

recursion.zig

[class]{}-[func]{recur}

recursion.dart

/* 递归 */
int recur(int n) {
  // 终止条件
  if (n == 1) return 1;
  // 递：递归调用
  int res = recur(n - 1);
  // 归：返回结果
  return n + res;
}

recursion.rs

[class]{}-[func]{recur}

图 2-3 展示了该函数的递归过程。

图 2-3   求和函数的递归过程

虽然从计算角度看，迭代与递归可以得到相同的结果，但它们代表了两种完全不同的思考和解决问题的范式。

• 迭代：“自下而上”地解决问题。从最基础的步骤开始，然后不断重复或累加这些步骤，直到任务完成。
• 递归：“自上而下”地解决问题。将原问题分解为更小的子问题，这些子问题和原问题具有相同的形式。接下来将子问题继续分解为更小的子问题，直到基本情况时停止（基本情况的解是已知的）。

以上述的求和函数为例，设问题 \(f(n) = 1 + 2 + \dots + n\) 。

• 迭代：在循环中模拟求和过程，从 \(1\) 遍历到 \(n\) ，每轮执行求和操作，即可求得 \(f(n)\) 。
• 递归：将问题分解为子问题 \(f(n) = n + f(n-1)\) ，不断（递归地）分解下去，直至基本情况 \(f(0) = 0\) 时终止。

1.   调用栈

递归函数每次调用自身时，系统都会为新开启的函数分配内存，以存储局部变量、调用地址和其他信息等。这将导致两方面的结果。

• 函数的上下文数据都存储在称为“栈帧空间”的内存区域中，直至函数返回后才会被释放。因此，递归通常比迭代更加耗费内存空间。
• 递归调用函数会产生额外的开销。因此递归通常比循环的时间效率更低。

如图 2-4 所示，在触发终止条件前，同时存在 \(n\) 个未返回的递归函数，递归深度为 \(n\) 。

图 2-4   递归调用深度

在实际中，编程语言允许的递归深度通常是有限的，过深的递归可能导致栈溢出报错。

2.   尾递归

有趣的是，如果函数在返回前的最后一步才进行递归调用，则该函数可以被编译器或解释器优化，使其在空间效率上与迭代相当。这种情况被称为「尾递归 tail recursion」。

• 普通递归：当函数返回到上一层级的函数后，需要继续执行代码，因此系统需要保存上一层调用的上下文。
• 尾递归：递归调用是函数返回前的最后一个操作，这意味着函数返回到上一层级后，无需继续执行其他操作，因此系统无需保存上一层函数的上下文。

以计算 \(1 + 2 + \dots + n\) 为例，我们可以将结果变量 res 设为函数参数，从而实现尾递归。

JavaC++PythonGoJSTSCC#SwiftZigDartRust

recursion.java

/* 尾递归 */
int tailRecur(int n, int res) {
    // 终止条件
    if (n == 0)
        return res;
    // 尾递归调用
    return tailRecur(n - 1, res + n);
}

recursion.cpp

/* 尾递归 */
int tailRecur(int n, int res) {
    // 终止条件
    if (n == 0)
        return res;
    // 尾递归调用
    return tailRecur(n - 1, res + n);
}

recursion.py

def tail_recur(n, res):
    """尾递归"""
    # 终止条件
    if n == 0:
        return res
    # 尾递归调用
    return tail_recur(n - 1, res + n)

recursion.go

[class]{}-[func]{tailRecur}

recursion.js

[class]{}-[func]{tailRecur}

recursion.ts

[class]{}-[func]{tailRecur}

recursion.c

[class]{}-[func]{tailRecur}

recursion.cs

[class]{recursion}-[func]{tailRecur}

recursion.swift

[class]{}-[func]{tailRecur}

recursion.zig

[class]{}-[func]{tailRecur}

recursion.dart

/* 尾递归 */
int tailRecur(int n, int res) {
  // 终止条件
  if (n == 0) return res;
  // 尾递归调用
  return tailRecur(n - 1, res + n);
}

recursion.rs

[class]{}-[func]{tail_recur}

两种递归的过程对比如图 2-5 所示。

• 普通递归：求和操作是在“归”的过程中执行的，每层返回后都要再执行一次求和操作。
• 尾递归：求和操作是在“递”的过程中执行的，“归”的过程只需层层返回。

图 2-5   尾递归过程

请注意，许多编译器或解释器并不支持尾递归优化。例如，Python 默认不支持尾递归优化，因此即使函数是尾递归形式，但仍然可能会遇到栈溢出问题。

3.   递归树

当处理与“分治”相关的算法问题时，递归往往比迭代的思路更加直观、代码更加易读。以“斐波那契数列”为例。

Question

给定一个斐波那契数列 \(0, 1, 1, 2, 3, 5, 8, 13, \dots\) ，求该数列的第 \(n\) 个数字。

设斐波那契数列的第 \(n\) 个数字为 \(f(n)\) ，易得两个结论。

• 数列的前两个数字为 \(f(1) = 0\) 和 \(f(2) = 1\) 。
• 数列中的每个数字是前两个数字的和，即 \(f(n) = f(n - 1) + f(n - 2)\) 。

按照递推关系进行递归调用，将前两个数字作为终止条件，便可写出递归代码。调用 fib(n) 即可得到斐波那契数列的第 \(n\) 个数字。

JavaC++PythonGoJSTSCC#SwiftZigDartRust

recursion.java

/* 斐波那契数列：递归 */
int fib(int n) {
    // 终止条件 f(1) = 0, f(2) = 1
    if (n == 1 || n == 2)
        return n - 1;
    // 递归调用 f(n) = f(n-1) + f(n-2)
    int res = fib(n - 1) + fib(n - 2);
    // 返回结果 f(n)
    return res;
}

recursion.cpp

/* 斐波那契数列：递归 */
int fib(int n) {
    // 终止条件 f(1) = 0, f(2) = 1
    if (n == 1 || n == 2)
        return n - 1;
    // 递归调用 f(n) = f(n-1) + f(n-2)
    int res = fib(n - 1) + fib(n - 2);
    // 返回结果 f(n)
    return res;
}

recursion.py

def fib(n: int) -> int:
    """斐波那契数列：递归"""
    # 终止条件 f(1) = 0, f(2) = 1
    if n == 1 or n == 2:
        return n - 1
    # 递归调用 f(n) = f(n-1) + f(n-2)
    res = fib(n - 1) + fib(n - 2)
    # 返回结果 f(n)
    return res

recursion.go

[class]{}-[func]{fib}

recursion.js

[class]{}-[func]{fib}

recursion.ts

[class]{}-[func]{fib}

recursion.c

[class]{}-[func]{fib}

recursion.cs

[class]{recursion}-[func]{fib}

recursion.swift

[class]{}-[func]{fib}

recursion.zig

[class]{}-[func]{fib}

recursion.dart

/* 斐波那契数列：递归 */
int fib(int n) {
  // 终止条件 f(1) = 0, f(2) = 1
  if (n == 1 || n == 2) return n - 1;
  // 递归调用 f(n) = f(n-1) + f(n-2)
  int res = fib(n - 1) + fib(n - 2);
  // 返回结果 f(n)
  return res;
}

recursion.rs

[class]{}-[func]{fib}

观察以上代码，我们在函数内递归调用了两个函数，这意味着从一个调用产生了两个调用分支。如图 2-6 所示，这样不断递归调用下去，最终将产生一个层数为 \(n\) 的「递归树 recursion tree」。

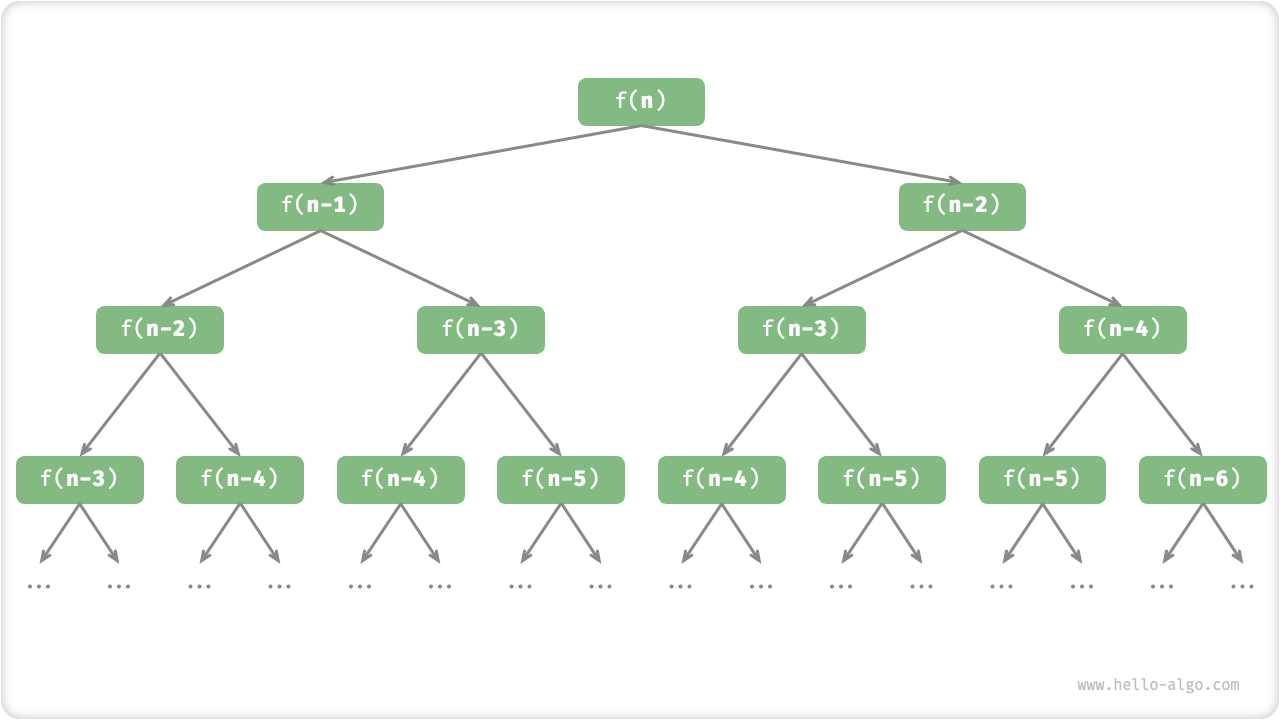
图 2-6   斐波那契数列的递归树

本质上看，递归体现“将问题分解为更小子问题”的思维范式，这种分治策略是至关重要的。

• 从算法角度看，搜索、排序、回溯、分治、动态规划等许多重要算法策略都直接或间接地应用这种思维方式。
• 从数据结构角度看，递归天然适合处理链表、树和图的相关问题，因为它们非常适合用分治思想进行分析。

评论