13.2   Permutation problem

The permutation problem is a typical application of the backtracking algorithm. It is defined as finding all possible arrangements of elements from a given set (such as an array or string).

Table 13-2 lists several example data, including the input arrays and their corresponding permutations.

Table 13-2   Permutation examples

Input array	Permutations
\([1]\)	\([1]\)
\([1, 2]\)	\([1, 2], [2, 1]\)
\([1, 2, 3]\)	\([1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2], [3, 2, 1]\)

13.2.1   Cases without equal elements

Question

Enter an integer array without duplicate elements and return all possible permutations.

From the perspective of the backtracking algorithm, we can imagine the process of generating permutations as a series of choices. Suppose the input array is \([1, 2, 3]\), if we first choose \(1\), then \(3\), and finally \(2\), we obtain the permutation \([1, 3, 2]\). Backtracking means undoing a choice and then continuing to try other choices.

From the code perspective, the candidate set choices contains all elements of the input array, and the state state contains elements that have been selected so far. Please note that each element can only be chosen once, thus all elements in state must be unique.

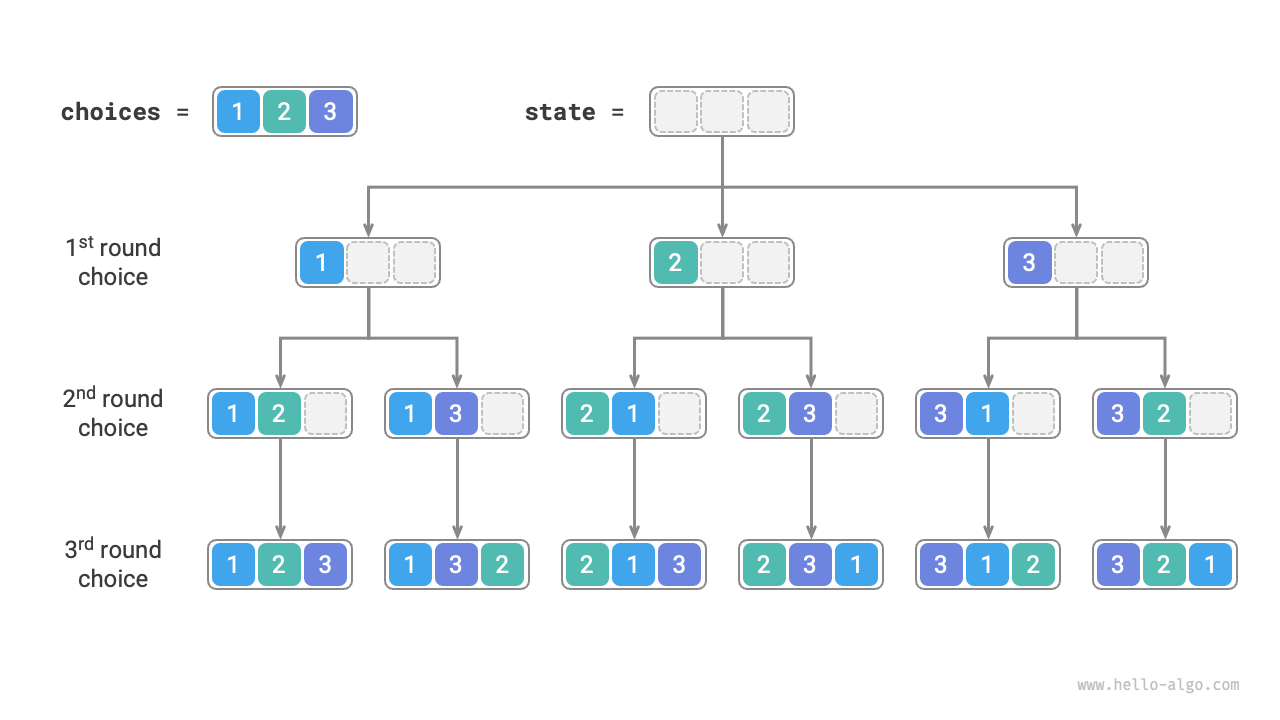
As shown in Figure 13-5, we can unfold the search process into a recursive tree, where each node represents the current state state. Starting from the root node, after three rounds of choices, we reach the leaf nodes, each corresponding to a permutation.

Figure 13-5   Permutation recursive tree

1.   Pruning of repeated choices

To ensure that each element is selected only once, we consider introducing a boolean array selected, where selected[i] indicates whether choices[i] has been selected. We base our pruning operations on this array:

• After making the choice choice[i], we set selected[i] to \(\text{True}\), indicating it has been chosen.
• When iterating through the choice list choices, skip all nodes that have already been selected, i.e., prune.

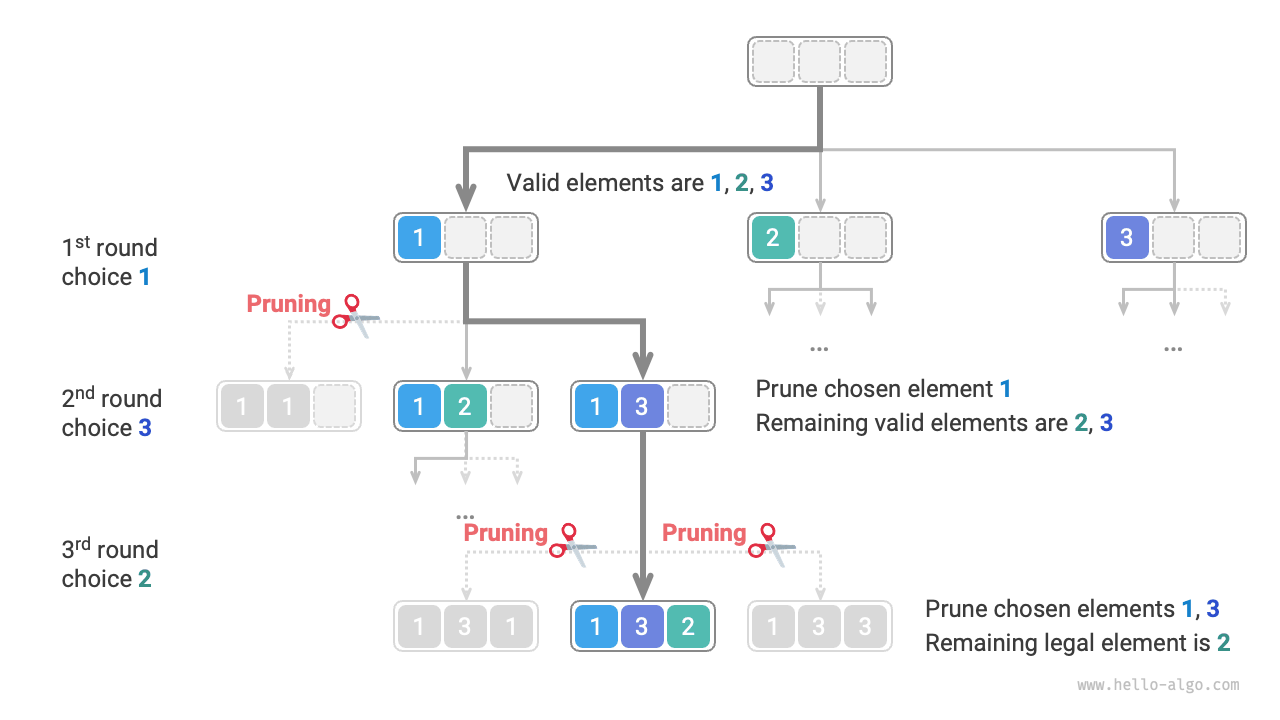
As shown in Figure 13-6, suppose we choose 1 in the first round, 3 in the second round, and 2 in the third round, we need to prune the branch of element 1 in the second round and elements 1 and 3 in the third round.

Figure 13-6   Permutation pruning example

Observing Figure 13-6, this pruning operation reduces the search space size from \(O(n^n)\) to \(O(n!)\).

2.   Code implementation

After understanding the above information, we can "fill in the blanks" in the framework code. To shorten the overall code, we do not implement individual functions within the framework code separately, but expand them in the backtrack() function:

PythonC++JavaC#GoSwiftJSTSDartRustCKotlinRubyZig

permutations_i.py

def backtrack(
    state: list[int], choices: list[int], selected: list[bool], res: list[list[int]]
):
    """回溯算法：全排列 I"""
    # 当状态长度等于元素数量时，记录解
    if len(state) == len(choices):
        res.append(list(state))
        return
    # 遍历所有选择
    for i, choice in enumerate(choices):
        # 剪枝：不允许重复选择元素
        if not selected[i]:
            # 尝试：做出选择，更新状态
            selected[i] = True
            state.append(choice)
            # 进行下一轮选择
            backtrack(state, choices, selected, res)
            # 回退：撤销选择，恢复到之前的状态
            selected[i] = False
            state.pop()

def permutations_i(nums: list[int]) -> list[list[int]]:
    """全排列 I"""
    res = []
    backtrack(state=[], choices=nums, selected=[False] * len(nums), res=res)
    return res

permutations_i.cpp

/* 回溯算法：全排列 I */
void backtrack(vector<int> &state, const vector<int> &choices, vector<bool> &selected, vector<vector<int>> &res) {
    // 当状态长度等于元素数量时，记录解
    if (state.size() == choices.size()) {
        res.push_back(state);
        return;
    }
    // 遍历所有选择
    for (int i = 0; i < choices.size(); i++) {
        int choice = choices[i];
        // 剪枝：不允许重复选择元素
        if (!selected[i]) {
            // 尝试：做出选择，更新状态
            selected[i] = true;
            state.push_back(choice);
            // 进行下一轮选择
            backtrack(state, choices, selected, res);
            // 回退：撤销选择，恢复到之前的状态
            selected[i] = false;
            state.pop_back();
        }
    }
}

/* 全排列 I */
vector<vector<int>> permutationsI(vector<int> nums) {
    vector<int> state;
    vector<bool> selected(nums.size(), false);
    vector<vector<int>> res;
    backtrack(state, nums, selected, res);
    return res;
}

permutations_i.java

/* 回溯算法：全排列 I */
void backtrack(List<Integer> state, int[] choices, boolean[] selected, List<List<Integer>> res) {
    // 当状态长度等于元素数量时，记录解
    if (state.size() == choices.length) {
        res.add(new ArrayList<Integer>(state));
        return;
    }
    // 遍历所有选择
    for (int i = 0; i < choices.length; i++) {
        int choice = choices[i];
        // 剪枝：不允许重复选择元素
        if (!selected[i]) {
            // 尝试：做出选择，更新状态
            selected[i] = true;
            state.add(choice);
            // 进行下一轮选择
            backtrack(state, choices, selected, res);
            // 回退：撤销选择，恢复到之前的状态
            selected[i] = false;
            state.remove(state.size() - 1);
        }
    }
}

/* 全排列 I */
List<List<Integer>> permutationsI(int[] nums) {
    List<List<Integer>> res = new ArrayList<List<Integer>>();
    backtrack(new ArrayList<Integer>(), nums, new boolean[nums.length], res);
    return res;
}

permutations_i.cs

/* 回溯算法：全排列 I */
void Backtrack(List<int> state, int[] choices, bool[] selected, List<List<int>> res) {
    // 当状态长度等于元素数量时，记录解
    if (state.Count == choices.Length) {
        res.Add(new List<int>(state));
        return;
    }
    // 遍历所有选择
    for (int i = 0; i < choices.Length; i++) {
        int choice = choices[i];
        // 剪枝：不允许重复选择元素
        if (!selected[i]) {
            // 尝试：做出选择，更新状态
            selected[i] = true;
            state.Add(choice);
            // 进行下一轮选择
            Backtrack(state, choices, selected, res);
            // 回退：撤销选择，恢复到之前的状态
            selected[i] = false;
            state.RemoveAt(state.Count - 1);
        }
    }
}

/* 全排列 I */
List<List<int>> PermutationsI(int[] nums) {
    List<List<int>> res = [];
    Backtrack([], nums, new bool[nums.Length], res);
    return res;
}

permutations_i.go

/* 回溯算法：全排列 I */
func backtrackI(state *[]int, choices *[]int, selected *[]bool, res *[][]int) {
    // 当状态长度等于元素数量时，记录解
    if len(*state) == len(*choices) {
        newState := append([]int{}, *state...)
        *res = append(*res, newState)
    }
    // 遍历所有选择
    for i := 0; i < len(*choices); i++ {
        choice := (*choices)[i]
        // 剪枝：不允许重复选择元素
        if !(*selected)[i] {
            // 尝试：做出选择，更新状态
            (*selected)[i] = true
            *state = append(*state, choice)
            // 进行下一轮选择
            backtrackI(state, choices, selected, res)
            // 回退：撤销选择，恢复到之前的状态
            (*selected)[i] = false
            *state = (*state)[:len(*state)-1]
        }
    }
}

/* 全排列 I */
func permutationsI(nums []int) [][]int {
    res := make([][]int, 0)
    state := make([]int, 0)
    selected := make([]bool, len(nums))
    backtrackI(&state, &nums, &selected, &res)
    return res
}

permutations_i.swift

/* 回溯算法：全排列 I */
func backtrack(state: inout [Int], choices: [Int], selected: inout [Bool], res: inout [[Int]]) {
    // 当状态长度等于元素数量时，记录解
    if state.count == choices.count {
        res.append(state)
        return
    }
    // 遍历所有选择
    for (i, choice) in choices.enumerated() {
        // 剪枝：不允许重复选择元素
        if !selected[i] {
            // 尝试：做出选择，更新状态
            selected[i] = true
            state.append(choice)
            // 进行下一轮选择
            backtrack(state: &state, choices: choices, selected: &selected, res: &res)
            // 回退：撤销选择，恢复到之前的状态
            selected[i] = false
            state.removeLast()
        }
    }
}

/* 全排列 I */
func permutationsI(nums: [Int]) -> [[Int]] {
    var state: [Int] = []
    var selected = Array(repeating: false, count: nums.count)
    var res: [[Int]] = []
    backtrack(state: &state, choices: nums, selected: &selected, res: &res)
    return res
}

permutations_i.js

/* 回溯算法：全排列 I */
function backtrack(state, choices, selected, res) {
    // 当状态长度等于元素数量时，记录解
    if (state.length === choices.length) {
        res.push([...state]);
        return;
    }
    // 遍历所有选择
    choices.forEach((choice, i) => {
        // 剪枝：不允许重复选择元素
        if (!selected[i]) {
            // 尝试：做出选择，更新状态
            selected[i] = true;
            state.push(choice);
            // 进行下一轮选择
            backtrack(state, choices, selected, res);
            // 回退：撤销选择，恢复到之前的状态
            selected[i] = false;
            state.pop();
        }
    });
}

/* 全排列 I */
function permutationsI(nums) {
    const res = [];
    backtrack([], nums, Array(nums.length).fill(false), res);
    return res;
}

permutations_i.ts

/* 回溯算法：全排列 I */
function backtrack(
    state: number[],
    choices: number[],
    selected: boolean[],
    res: number[][]
): void {
    // 当状态长度等于元素数量时，记录解
    if (state.length === choices.length) {
        res.push([...state]);
        return;
    }
    // 遍历所有选择
    choices.forEach((choice, i) => {
        // 剪枝：不允许重复选择元素
        if (!selected[i]) {
            // 尝试：做出选择，更新状态
            selected[i] = true;
            state.push(choice);
            // 进行下一轮选择
            backtrack(state, choices, selected, res);
            // 回退：撤销选择，恢复到之前的状态
            selected[i] = false;
            state.pop();
        }
    });
}

/* 全排列 I */
function permutationsI(nums: number[]): number[][] {
    const res: number[][] = [];
    backtrack([], nums, Array(nums.length).fill(false), res);
    return res;
}

permutations_i.dart

/* 回溯算法：全排列 I */
void backtrack(
  List<int> state,
  List<int> choices,
  List<bool> selected,
  List<List<int>> res,
) {
  // 当状态长度等于元素数量时，记录解
  if (state.length == choices.length) {
    res.add(List.from(state));
    return;
  }
  // 遍历所有选择
  for (int i = 0; i < choices.length; i++) {
    int choice = choices[i];
    // 剪枝：不允许重复选择元素
    if (!selected[i]) {
      // 尝试：做出选择，更新状态
      selected[i] = true;
      state.add(choice);
      // 进行下一轮选择
      backtrack(state, choices, selected, res);
      // 回退：撤销选择，恢复到之前的状态
      selected[i] = false;
      state.removeLast();
    }
  }
}

/* 全排列 I */
List<List<int>> permutationsI(List<int> nums) {
  List<List<int>> res = [];
  backtrack([], nums, List.filled(nums.length, false), res);
  return res;
}

permutations_i.rs

/* 回溯算法：全排列 I */
fn backtrack(mut state: Vec<i32>, choices: &[i32], selected: &mut [bool], res: &mut Vec<Vec<i32>>) {
    // 当状态长度等于元素数量时，记录解
    if state.len() == choices.len() {
        res.push(state);
        return;
    }
    // 遍历所有选择
    for i in 0..choices.len() {
        let choice = choices[i];
        // 剪枝：不允许重复选择元素
        if !selected[i] {
            // 尝试：做出选择，更新状态
            selected[i] = true;
            state.push(choice);
            // 进行下一轮选择
            backtrack(state.clone(), choices, selected, res);
            // 回退：撤销选择，恢复到之前的状态
            selected[i] = false;
            state.remove(state.len() - 1);
        }
    }
}

/* 全排列 I */
fn permutations_i(nums: &mut [i32]) -> Vec<Vec<i32>> {
    let mut res = Vec::new(); // 状态（子集）
    backtrack(Vec::new(), nums, &mut vec![false; nums.len()], &mut res);
    res
}

permutations_i.c

/* 回溯算法：全排列 I */
void backtrack(int *state, int stateSize, int *choices, int choicesSize, bool *selected, int **res, int *resSize) {
    // 当状态长度等于元素数量时，记录解
    if (stateSize == choicesSize) {
        res[*resSize] = (int *)malloc(choicesSize * sizeof(int));
        for (int i = 0; i < choicesSize; i++) {
            res[*resSize][i] = state[i];
        }
        (*resSize)++;
        return;
    }
    // 遍历所有选择
    for (int i = 0; i < choicesSize; i++) {
        int choice = choices[i];
        // 剪枝：不允许重复选择元素
        if (!selected[i]) {
            // 尝试：做出选择，更新状态
            selected[i] = true;
            state[stateSize] = choice;
            // 进行下一轮选择
            backtrack(state, stateSize + 1, choices, choicesSize, selected, res, resSize);
            // 回退：撤销选择，恢复到之前的状态
            selected[i] = false;
        }
    }
}

/* 全排列 I */
int **permutationsI(int *nums, int numsSize, int *returnSize) {
    int *state = (int *)malloc(numsSize * sizeof(int));
    bool *selected = (bool *)malloc(numsSize * sizeof(bool));
    for (int i = 0; i < numsSize; i++) {
        selected[i] = false;
    }
    int **res = (int **)malloc(MAX_SIZE * sizeof(int *));
    *returnSize = 0;

    backtrack(state, 0, nums, numsSize, selected, res, returnSize);

    free(state);
    free(selected);

    return res;
}

permutations_i.kt

/* 回溯算法：全排列 I */
fun backtrack(
    state: MutableList<Int>,
    choices: IntArray,
    selected: BooleanArray,
    res: MutableList<MutableList<Int>?>
) {
    // 当状态长度等于元素数量时，记录解
    if (state.size == choices.size) {
        res.add(state.toMutableList())
        return
    }
    // 遍历所有选择
    for (i in choices.indices) {
        val choice = choices[i]
        // 剪枝：不允许重复选择元素
        if (!selected[i]) {
            // 尝试：做出选择，更新状态
            selected[i] = true
            state.add(choice)
            // 进行下一轮选择
            backtrack(state, choices, selected, res)
            // 回退：撤销选择，恢复到之前的状态
            selected[i] = false
            state.removeAt(state.size - 1)
        }
    }
}

/* 全排列 I */
fun permutationsI(nums: IntArray): MutableList<MutableList<Int>?> {
    val res = mutableListOf<MutableList<Int>?>()
    backtrack(mutableListOf(), nums, BooleanArray(nums.size), res)
    return res
}

permutations_i.rb

[class]{}-[func]{backtrack}

[class]{}-[func]{permutations_i}

permutations_i.zig

[class]{}-[func]{backtrack}

[class]{}-[func]{permutationsI}

Code Visualization

Full Screen >

13.2.2   Considering cases with equal elements

Question

Enter an integer array, which may contain duplicate elements, and return all unique permutations.

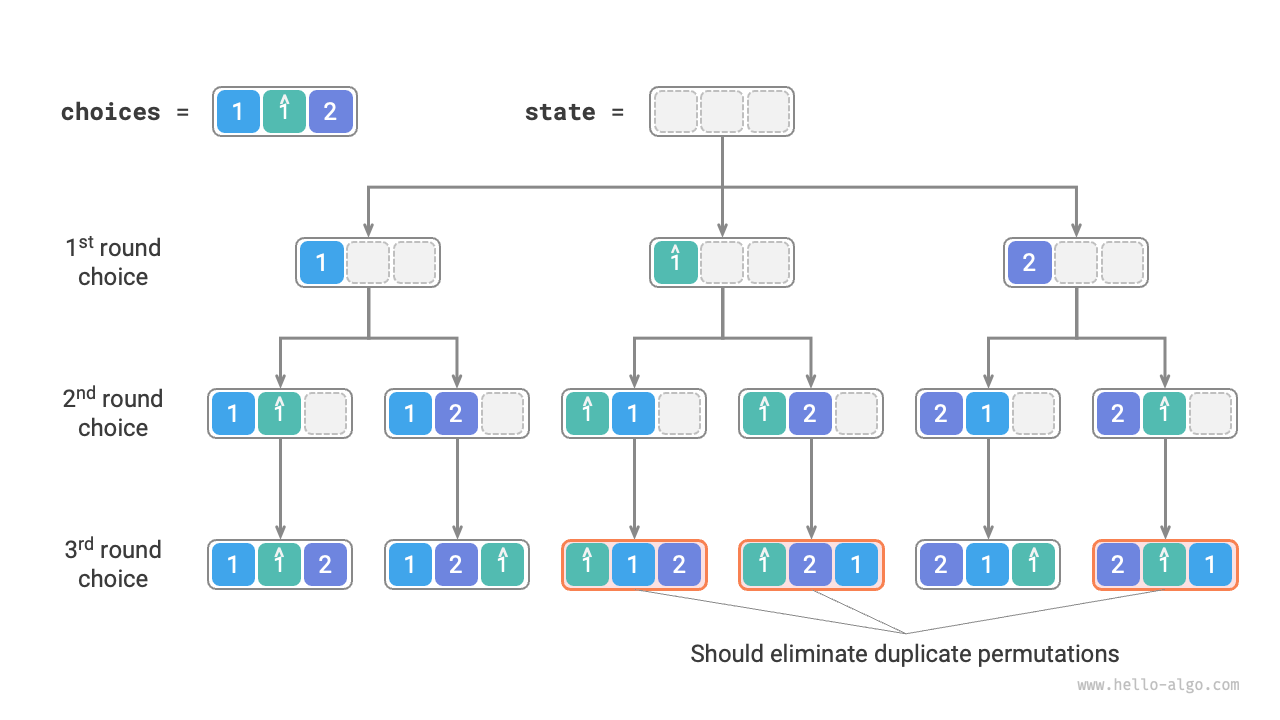
Suppose the input array is \([1, 1, 2]\). To differentiate the two duplicate elements \(1\), we mark the second \(1\) as \(\hat{1}\).

As shown in Figure 13-7, half of the permutations generated by the above method are duplicates.

Figure 13-7   Duplicate permutations

So, how do we eliminate duplicate permutations? Most directly, consider using a hash set to deduplicate permutation results. However, this is not elegant, as branches generating duplicate permutations are unnecessary and should be identified and pruned in advance, which can further improve algorithm efficiency.

1.   Pruning of equal elements

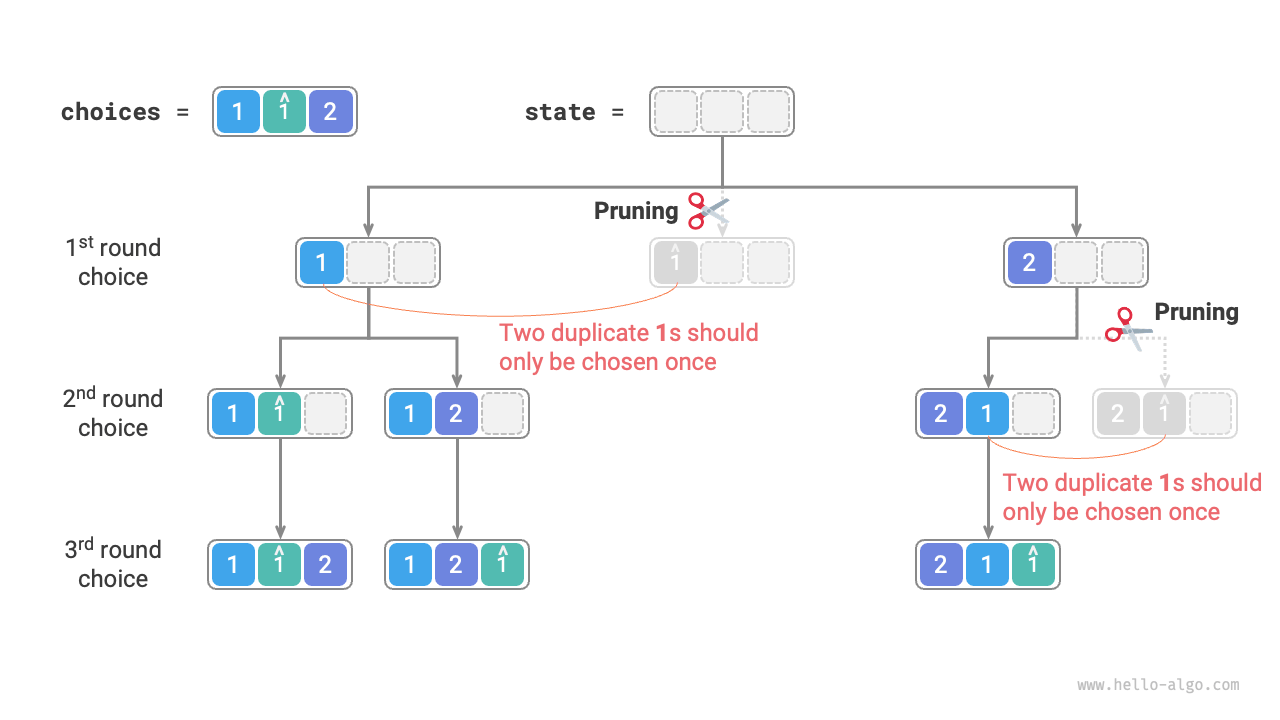
Observing Figure 13-8, in the first round, choosing \(1\) or \(\hat{1}\) results in identical permutations under both choices, thus we should prune \(\hat{1}\).

Similarly, after choosing \(2\) in the first round, choosing \(1\) and \(\hat{1}\) in the second round also produces duplicate branches, so we should also prune \(\hat{1}\) in the second round.

Essentially, our goal is to ensure that multiple equal elements are only selected once in each round of choices.

Figure 13-8   Duplicate permutations pruning

2.   Code implementation

Based on the code from the previous problem, we consider initiating a hash set duplicated in each round of choices, used to record elements that have been tried in that round, and prune duplicate elements:

PythonC++JavaC#GoSwiftJSTSDartRustCKotlinRubyZig

permutations_ii.py

def backtrack(
    state: list[int], choices: list[int], selected: list[bool], res: list[list[int]]
):
    """回溯算法：全排列 II"""
    # 当状态长度等于元素数量时，记录解
    if len(state) == len(choices):
        res.append(list(state))
        return
    # 遍历所有选择
    duplicated = set[int]()
    for i, choice in enumerate(choices):
        # 剪枝：不允许重复选择元素 且 不允许重复选择相等元素
        if not selected[i] and choice not in duplicated:
            # 尝试：做出选择，更新状态
            duplicated.add(choice)  # 记录选择过的元素值
            selected[i] = True
            state.append(choice)
            # 进行下一轮选择
            backtrack(state, choices, selected, res)
            # 回退：撤销选择，恢复到之前的状态
            selected[i] = False
            state.pop()

def permutations_ii(nums: list[int]) -> list[list[int]]:
    """全排列 II"""
    res = []
    backtrack(state=[], choices=nums, selected=[False] * len(nums), res=res)
    return res

permutations_ii.cpp

/* 回溯算法：全排列 II */
void backtrack(vector<int> &state, const vector<int> &choices, vector<bool> &selected, vector<vector<int>> &res) {
    // 当状态长度等于元素数量时，记录解
    if (state.size() == choices.size()) {
        res.push_back(state);
        return;
    }
    // 遍历所有选择
    unordered_set<int> duplicated;
    for (int i = 0; i < choices.size(); i++) {
        int choice = choices[i];
        // 剪枝：不允许重复选择元素 且 不允许重复选择相等元素
        if (!selected[i] && duplicated.find(choice) == duplicated.end()) {
            // 尝试：做出选择，更新状态
            duplicated.emplace(choice); // 记录选择过的元素值
            selected[i] = true;
            state.push_back(choice);
            // 进行下一轮选择
            backtrack(state, choices, selected, res);
            // 回退：撤销选择，恢复到之前的状态
            selected[i] = false;
            state.pop_back();
        }
    }
}

/* 全排列 II */
vector<vector<int>> permutationsII(vector<int> nums) {
    vector<int> state;
    vector<bool> selected(nums.size(), false);
    vector<vector<int>> res;
    backtrack(state, nums, selected, res);
    return res;
}

permutations_ii.java

/* 回溯算法：全排列 II */
void backtrack(List<Integer> state, int[] choices, boolean[] selected, List<List<Integer>> res) {
    // 当状态长度等于元素数量时，记录解
    if (state.size() == choices.length) {
        res.add(new ArrayList<Integer>(state));
        return;
    }
    // 遍历所有选择
    Set<Integer> duplicated = new HashSet<Integer>();
    for (int i = 0; i < choices.length; i++) {
        int choice = choices[i];
        // 剪枝：不允许重复选择元素 且 不允许重复选择相等元素
        if (!selected[i] && !duplicated.contains(choice)) {
            // 尝试：做出选择，更新状态
            duplicated.add(choice); // 记录选择过的元素值
            selected[i] = true;
            state.add(choice);
            // 进行下一轮选择
            backtrack(state, choices, selected, res);
            // 回退：撤销选择，恢复到之前的状态
            selected[i] = false;
            state.remove(state.size() - 1);
        }
    }
}

/* 全排列 II */
List<List<Integer>> permutationsII(int[] nums) {
    List<List<Integer>> res = new ArrayList<List<Integer>>();
    backtrack(new ArrayList<Integer>(), nums, new boolean[nums.length], res);
    return res;
}

permutations_ii.cs

/* 回溯算法：全排列 II */
void Backtrack(List<int> state, int[] choices, bool[] selected, List<List<int>> res) {
    // 当状态长度等于元素数量时，记录解
    if (state.Count == choices.Length) {
        res.Add(new List<int>(state));
        return;
    }
    // 遍历所有选择
    HashSet<int> duplicated = [];
    for (int i = 0; i < choices.Length; i++) {
        int choice = choices[i];
        // 剪枝：不允许重复选择元素 且 不允许重复选择相等元素
        if (!selected[i] && !duplicated.Contains(choice)) {
            // 尝试：做出选择，更新状态
            duplicated.Add(choice); // 记录选择过的元素值
            selected[i] = true;
            state.Add(choice);
            // 进行下一轮选择
            Backtrack(state, choices, selected, res);
            // 回退：撤销选择，恢复到之前的状态
            selected[i] = false;
            state.RemoveAt(state.Count - 1);
        }
    }
}

/* 全排列 II */
List<List<int>> PermutationsII(int[] nums) {
    List<List<int>> res = [];
    Backtrack([], nums, new bool[nums.Length], res);
    return res;
}

permutations_ii.go

/* 回溯算法：全排列 II */
func backtrackII(state *[]int, choices *[]int, selected *[]bool, res *[][]int) {
    // 当状态长度等于元素数量时，记录解
    if len(*state) == len(*choices) {
        newState := append([]int{}, *state...)
        *res = append(*res, newState)
    }
    // 遍历所有选择
    duplicated := make(map[int]struct{}, 0)
    for i := 0; i < len(*choices); i++ {
        choice := (*choices)[i]
        // 剪枝：不允许重复选择元素 且 不允许重复选择相等元素
        if _, ok := duplicated[choice]; !ok && !(*selected)[i] {
            // 尝试：做出选择，更新状态
            // 记录选择过的元素值
            duplicated[choice] = struct{}{}
            (*selected)[i] = true
            *state = append(*state, choice)
            // 进行下一轮选择
            backtrackII(state, choices, selected, res)
            // 回退：撤销选择，恢复到之前的状态
            (*selected)[i] = false
            *state = (*state)[:len(*state)-1]
        }
    }
}

/* 全排列 II */
func permutationsII(nums []int) [][]int {
    res := make([][]int, 0)
    state := make([]int, 0)
    selected := make([]bool, len(nums))
    backtrackII(&state, &nums, &selected, &res)
    return res
}

permutations_ii.swift

/* 回溯算法：全排列 II */
func backtrack(state: inout [Int], choices: [Int], selected: inout [Bool], res: inout [[Int]]) {
    // 当状态长度等于元素数量时，记录解
    if state.count == choices.count {
        res.append(state)
        return
    }
    // 遍历所有选择
    var duplicated: Set<Int> = []
    for (i, choice) in choices.enumerated() {
        // 剪枝：不允许重复选择元素 且 不允许重复选择相等元素
        if !selected[i], !duplicated.contains(choice) {
            // 尝试：做出选择，更新状态
            duplicated.insert(choice) // 记录选择过的元素值
            selected[i] = true
            state.append(choice)
            // 进行下一轮选择
            backtrack(state: &state, choices: choices, selected: &selected, res: &res)
            // 回退：撤销选择，恢复到之前的状态
            selected[i] = false
            state.removeLast()
        }
    }
}

/* 全排列 II */
func permutationsII(nums: [Int]) -> [[Int]] {
    var state: [Int] = []
    var selected = Array(repeating: false, count: nums.count)
    var res: [[Int]] = []
    backtrack(state: &state, choices: nums, selected: &selected, res: &res)
    return res
}

permutations_ii.js

/* 回溯算法：全排列 II */
function backtrack(state, choices, selected, res) {
    // 当状态长度等于元素数量时，记录解
    if (state.length === choices.length) {
        res.push([...state]);
        return;
    }
    // 遍历所有选择
    const duplicated = new Set();
    choices.forEach((choice, i) => {
        // 剪枝：不允许重复选择元素 且 不允许重复选择相等元素
        if (!selected[i] && !duplicated.has(choice)) {
            // 尝试：做出选择，更新状态
            duplicated.add(choice); // 记录选择过的元素值
            selected[i] = true;
            state.push(choice);
            // 进行下一轮选择
            backtrack(state, choices, selected, res);
            // 回退：撤销选择，恢复到之前的状态
            selected[i] = false;
            state.pop();
        }
    });
}

/* 全排列 II */
function permutationsII(nums) {
    const res = [];
    backtrack([], nums, Array(nums.length).fill(false), res);
    return res;
}

permutations_ii.ts

/* 回溯算法：全排列 II */
function backtrack(
    state: number[],
    choices: number[],
    selected: boolean[],
    res: number[][]
): void {
    // 当状态长度等于元素数量时，记录解
    if (state.length === choices.length) {
        res.push([...state]);
        return;
    }
    // 遍历所有选择
    const duplicated = new Set();
    choices.forEach((choice, i) => {
        // 剪枝：不允许重复选择元素 且 不允许重复选择相等元素
        if (!selected[i] && !duplicated.has(choice)) {
            // 尝试：做出选择，更新状态
            duplicated.add(choice); // 记录选择过的元素值
            selected[i] = true;
            state.push(choice);
            // 进行下一轮选择
            backtrack(state, choices, selected, res);
            // 回退：撤销选择，恢复到之前的状态
            selected[i] = false;
            state.pop();
        }
    });
}

/* 全排列 II */
function permutationsII(nums: number[]): number[][] {
    const res: number[][] = [];
    backtrack([], nums, Array(nums.length).fill(false), res);
    return res;
}

permutations_ii.dart

/* 回溯算法：全排列 II */
void backtrack(
  List<int> state,
  List<int> choices,
  List<bool> selected,
  List<List<int>> res,
) {
  // 当状态长度等于元素数量时，记录解
  if (state.length == choices.length) {
    res.add(List.from(state));
    return;
  }
  // 遍历所有选择
  Set<int> duplicated = {};
  for (int i = 0; i < choices.length; i++) {
    int choice = choices[i];
    // 剪枝：不允许重复选择元素 且 不允许重复选择相等元素
    if (!selected[i] && !duplicated.contains(choice)) {
      // 尝试：做出选择，更新状态
      duplicated.add(choice); // 记录选择过的元素值
      selected[i] = true;
      state.add(choice);
      // 进行下一轮选择
      backtrack(state, choices, selected, res);
      // 回退：撤销选择，恢复到之前的状态
      selected[i] = false;
      state.removeLast();
    }
  }
}

/* 全排列 II */
List<List<int>> permutationsII(List<int> nums) {
  List<List<int>> res = [];
  backtrack([], nums, List.filled(nums.length, false), res);
  return res;
}

permutations_ii.rs

/* 回溯算法：全排列 II */
fn backtrack(mut state: Vec<i32>, choices: &[i32], selected: &mut [bool], res: &mut Vec<Vec<i32>>) {
    // 当状态长度等于元素数量时，记录解
    if state.len() == choices.len() {
        res.push(state);
        return;
    }
    // 遍历所有选择
    let mut duplicated = HashSet::<i32>::new();
    for i in 0..choices.len() {
        let choice = choices[i];
        // 剪枝：不允许重复选择元素 且 不允许重复选择相等元素
        if !selected[i] && !duplicated.contains(&choice) {
            // 尝试：做出选择，更新状态
            duplicated.insert(choice); // 记录选择过的元素值
            selected[i] = true;
            state.push(choice);
            // 进行下一轮选择
            backtrack(state.clone(), choices, selected, res);
            // 回退：撤销选择，恢复到之前的状态
            selected[i] = false;
            state.remove(state.len() - 1);
        }
    }
}

/* 全排列 II */
fn permutations_ii(nums: &mut [i32]) -> Vec<Vec<i32>> {
    let mut res = Vec::new();
    backtrack(Vec::new(), nums, &mut vec![false; nums.len()], &mut res);
    res
}

permutations_ii.c

/* 回溯算法：全排列 II */
void backtrack(int *state, int stateSize, int *choices, int choicesSize, bool *selected, int **res, int *resSize) {
    // 当状态长度等于元素数量时，记录解
    if (stateSize == choicesSize) {
        res[*resSize] = (int *)malloc(choicesSize * sizeof(int));
        for (int i = 0; i < choicesSize; i++) {
            res[*resSize][i] = state[i];
        }
        (*resSize)++;
        return;
    }
    // 遍历所有选择
    bool duplicated[MAX_SIZE] = {false};
    for (int i = 0; i < choicesSize; i++) {
        int choice = choices[i];
        // 剪枝：不允许重复选择元素 且 不允许重复选择相等元素
        if (!selected[i] && !duplicated[choice]) {
            // 尝试：做出选择，更新状态
            duplicated[choice] = true; // 记录选择过的元素值
            selected[i] = true;
            state[stateSize] = choice;
            // 进行下一轮选择
            backtrack(state, stateSize + 1, choices, choicesSize, selected, res, resSize);
            // 回退：撤销选择，恢复到之前的状态
            selected[i] = false;
        }
    }
}

/* 全排列 II */
int **permutationsII(int *nums, int numsSize, int *returnSize) {
    int *state = (int *)malloc(numsSize * sizeof(int));
    bool *selected = (bool *)malloc(numsSize * sizeof(bool));
    for (int i = 0; i < numsSize; i++) {
        selected[i] = false;
    }
    int **res = (int **)malloc(MAX_SIZE * sizeof(int *));
    *returnSize = 0;

    backtrack(state, 0, nums, numsSize, selected, res, returnSize);

    free(state);
    free(selected);

    return res;
}

permutations_ii.kt

/* 回溯算法：全排列 II */
fun backtrack(
    state: MutableList<Int>,
    choices: IntArray,
    selected: BooleanArray,
    res: MutableList<MutableList<Int>?>
) {
    // 当状态长度等于元素数量时，记录解
    if (state.size == choices.size) {
        res.add(state.toMutableList())
        return
    }
    // 遍历所有选择
    val duplicated = HashSet<Int>()
    for (i in choices.indices) {
        val choice = choices[i]
        // 剪枝：不允许重复选择元素 且 不允许重复选择相等元素
        if (!selected[i] && !duplicated.contains(choice)) {
            // 尝试：做出选择，更新状态
            duplicated.add(choice) // 记录选择过的元素值
            selected[i] = true
            state.add(choice)
            // 进行下一轮选择
            backtrack(state, choices, selected, res)
            // 回退：撤销选择，恢复到之前的状态
            selected[i] = false
            state.removeAt(state.size - 1)
        }
    }
}

/* 全排列 II */
fun permutationsII(nums: IntArray): MutableList<MutableList<Int>?> {
    val res = mutableListOf<MutableList<Int>?>()
    backtrack(mutableListOf(), nums, BooleanArray(nums.size), res)
    return res
}

permutations_ii.rb

[class]{}-[func]{backtrack}

[class]{}-[func]{permutations_ii}

permutations_ii.zig

[class]{}-[func]{backtrack}

[class]{}-[func]{permutationsII}

Code Visualization

Full Screen >

Assuming all elements are distinct from each other, there are \(n!\) (factorial) permutations of \(n\) elements; when recording results, it is necessary to copy a list of length \(n\), using \(O(n)\) time. Thus, the time complexity is \(O(n!n)\).

The maximum recursion depth is \(n\), using \(O(n)\) frame space. Selected uses \(O(n)\) space. At any one time, there can be up to \(n\) duplicated, using \(O(n^2)\) space. Therefore, the space complexity is \(O(n^2)\).

3.   Comparison of the two pruning methods

Please note, although both selected and duplicated are used for pruning, their targets are different.

• Repeated choice pruning: There is only one selected throughout the search process. It records which elements are currently in the state, aiming to prevent an element from appearing repeatedly in state.
• Equal element pruning: Each round of choices (each call to the backtrack function) contains a duplicated. It records which elements have been chosen in the current traversal (for loop), aiming to ensure equal elements are selected only once.

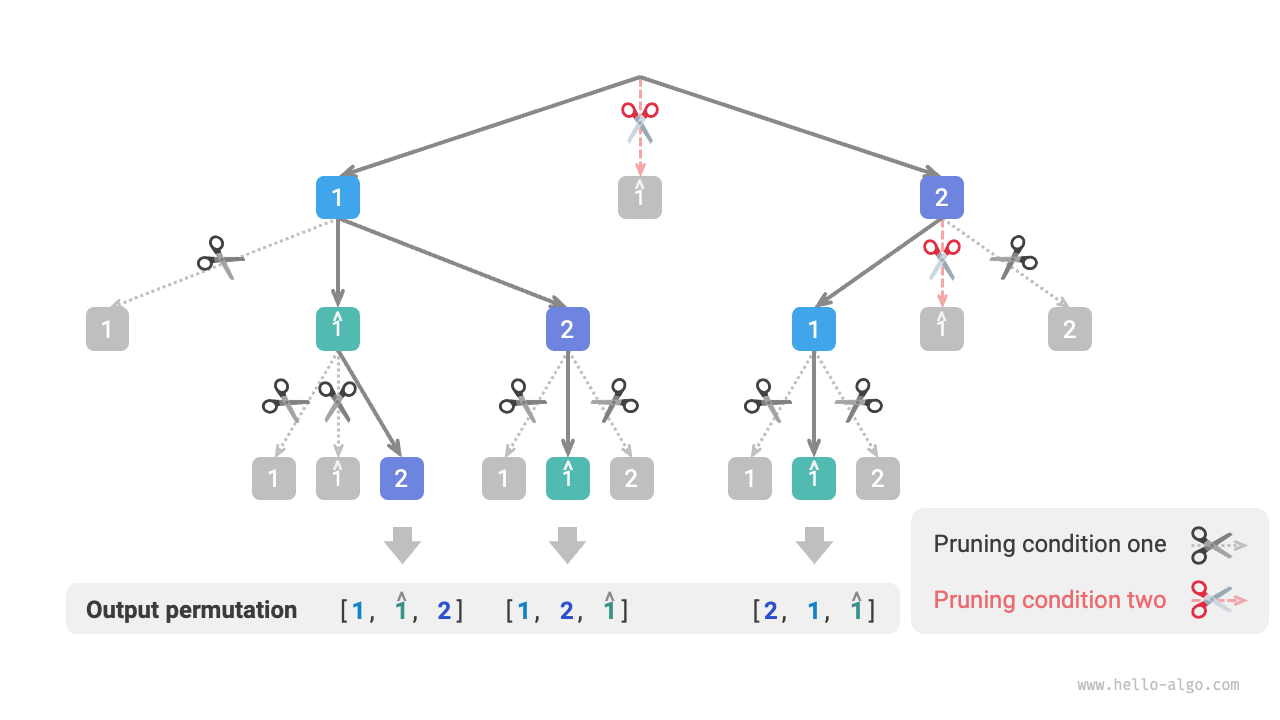
Figure 13-9 shows the scope of the two pruning conditions. Note, each node in the tree represents a choice, and the nodes from the root to the leaf form a permutation.

Figure 13-9   Scope of the two pruning conditions

Feel free to drop your insights, questions or suggestions