Skip to content

10.1   Binary search

Binary search is an efficient search algorithm based on the divide-and-conquer strategy. It utilizes the orderliness of data, reducing the search range by half each round until the target element is found or the search interval is empty.

Question

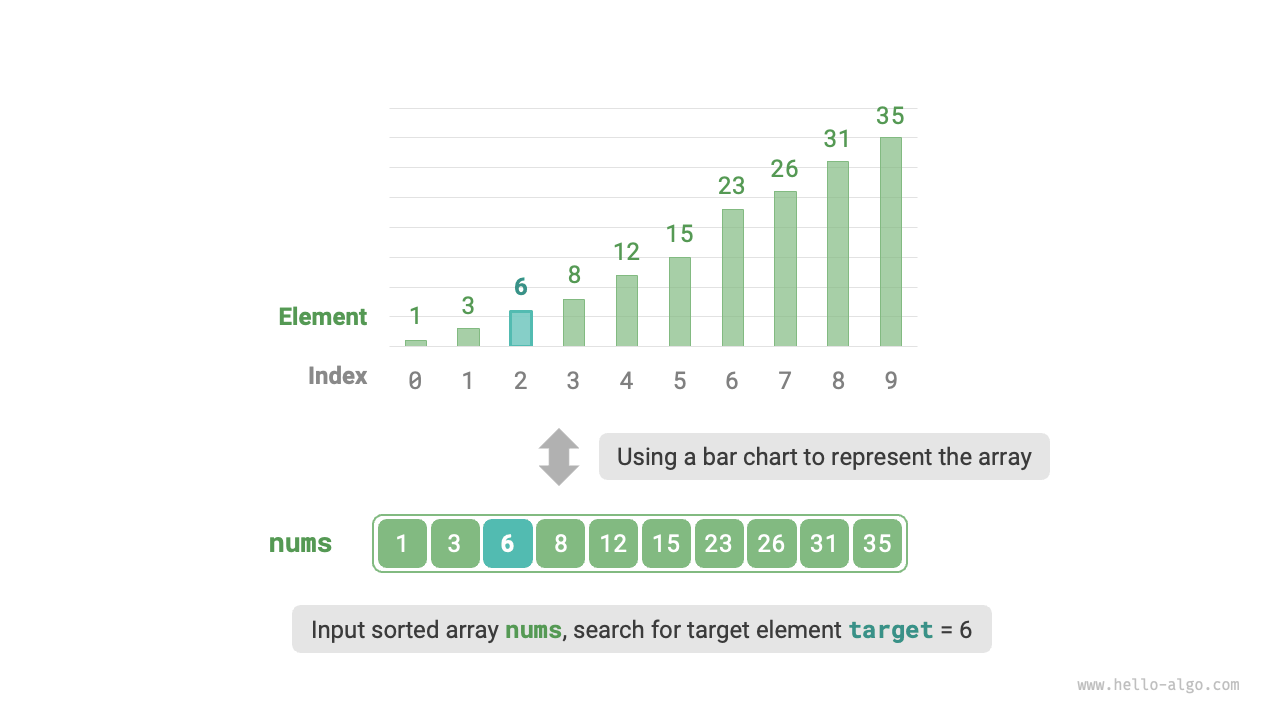
Given an array nums of length \(n\), with elements arranged in ascending order and non-repeating. Please find and return the index of element target in this array. If the array does not contain the element, return \(-1\). An example is shown in Figure 10-1.

Binary search example data

Figure 10-1   Binary search example data

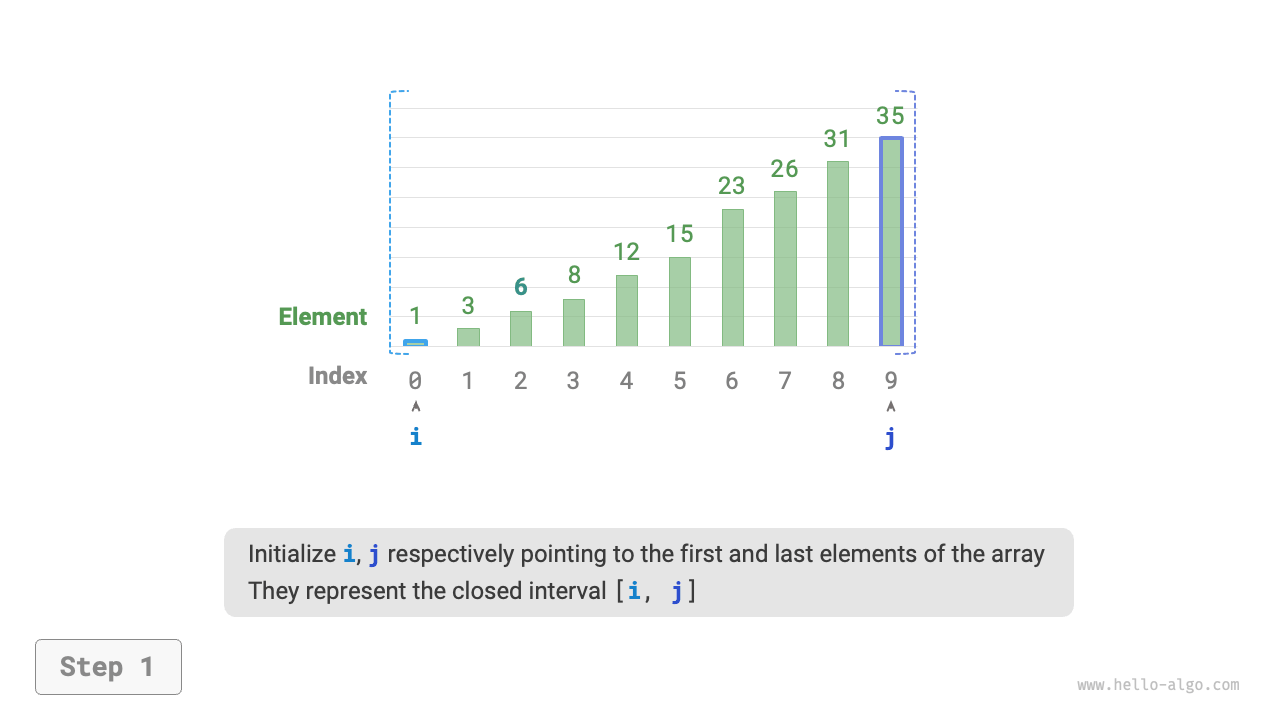
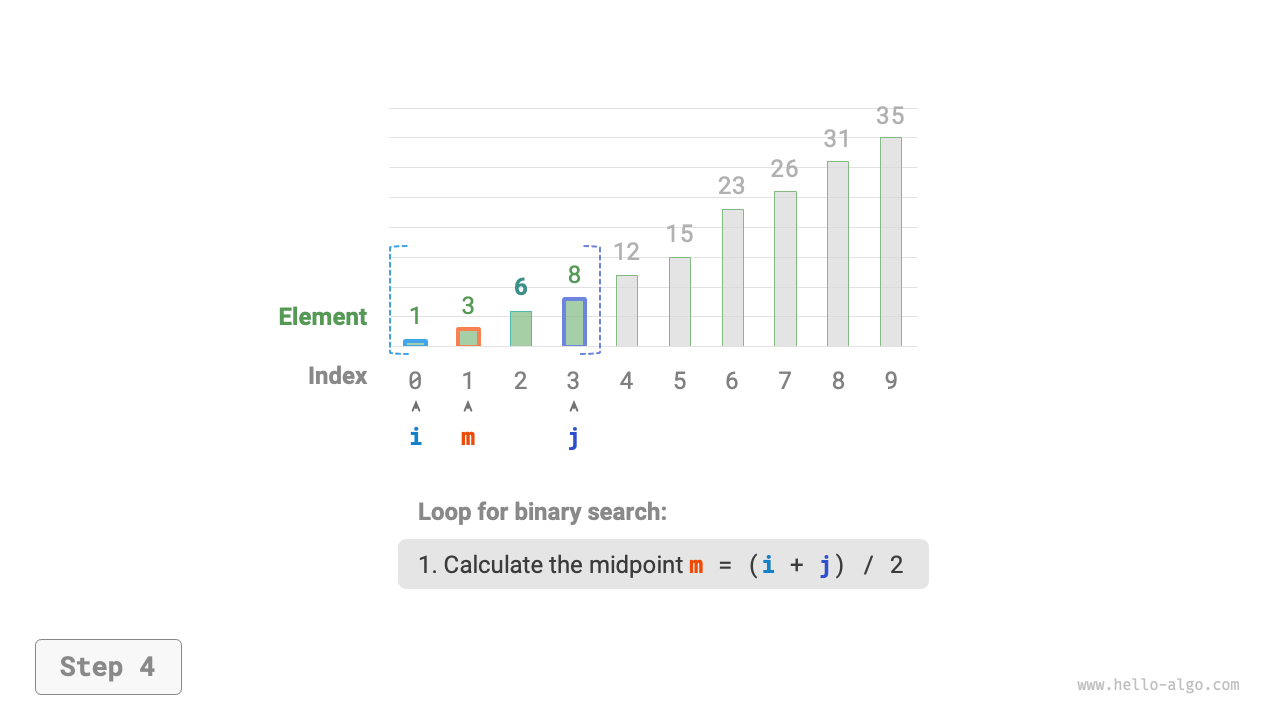
As shown in Figure 10-2, we first initialize pointers \(i = 0\) and \(j = n - 1\), pointing to the first and last elements of the array, representing the search interval \([0, n - 1]\). Please note that square brackets indicate a closed interval, which includes the boundary values themselves.

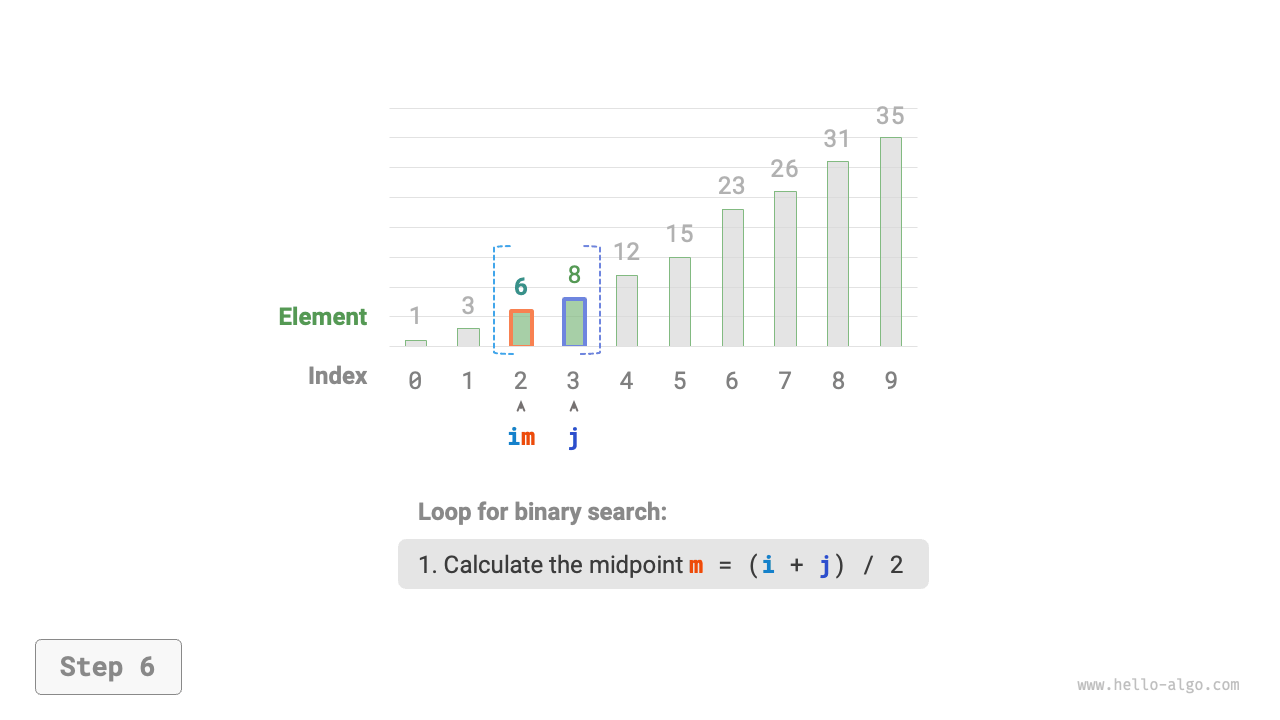
Next, perform the following two steps in a loop.

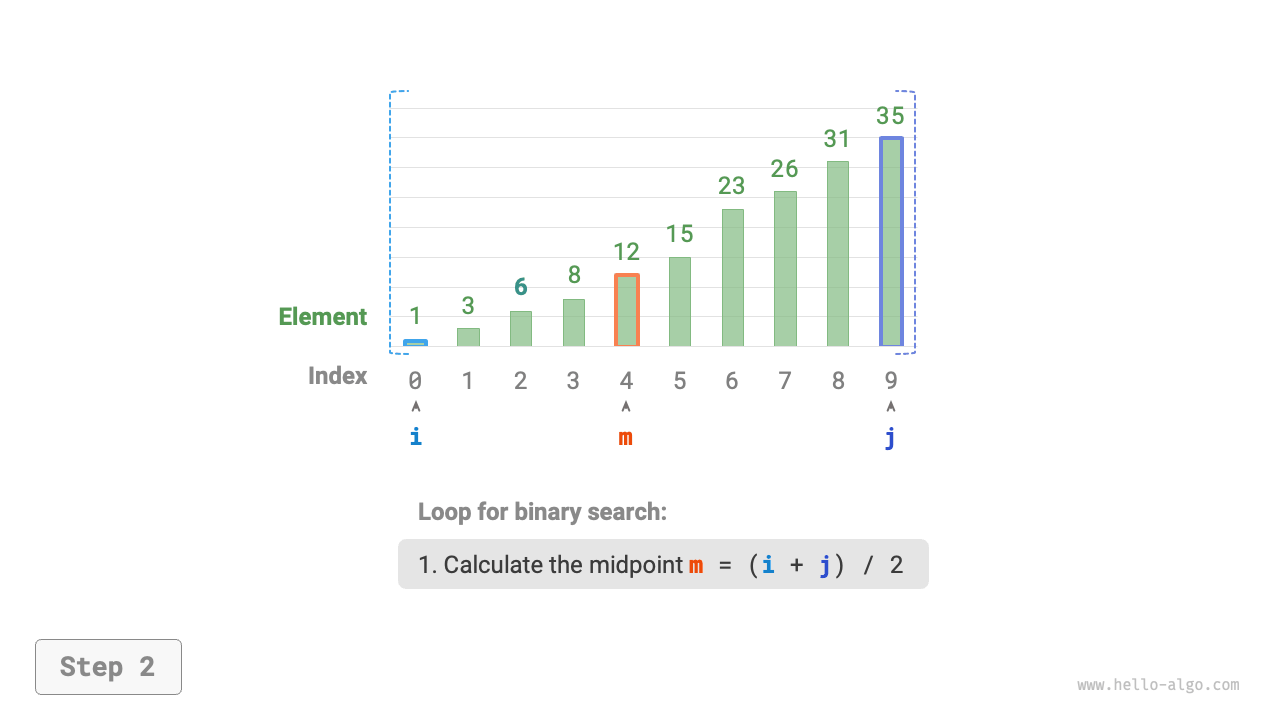
  1. Calculate the midpoint index \(m = \lfloor {(i + j) / 2} \rfloor\), where \(\lfloor \: \rfloor\) denotes the floor operation.
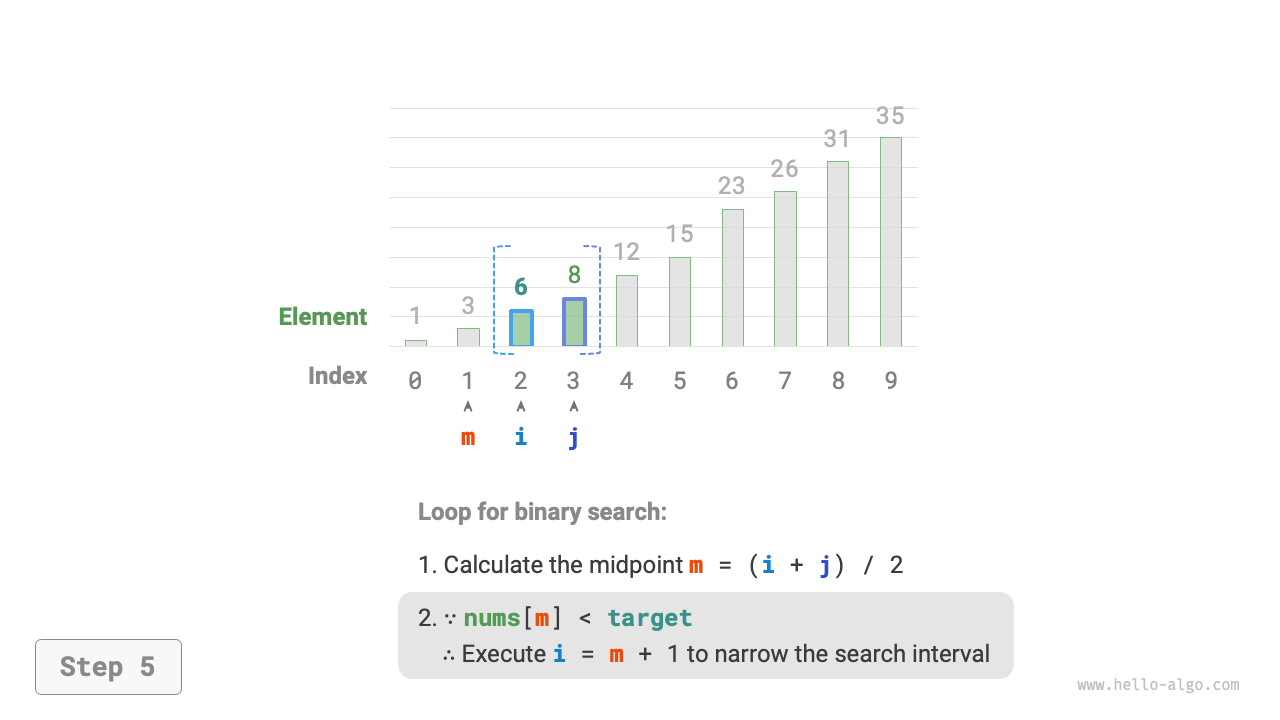
  2. Compare the size of nums[m] and target, divided into the following three scenarios.
    1. If nums[m] < target, it indicates that target is in the interval \([m + 1, j]\), thus set \(i = m + 1\).
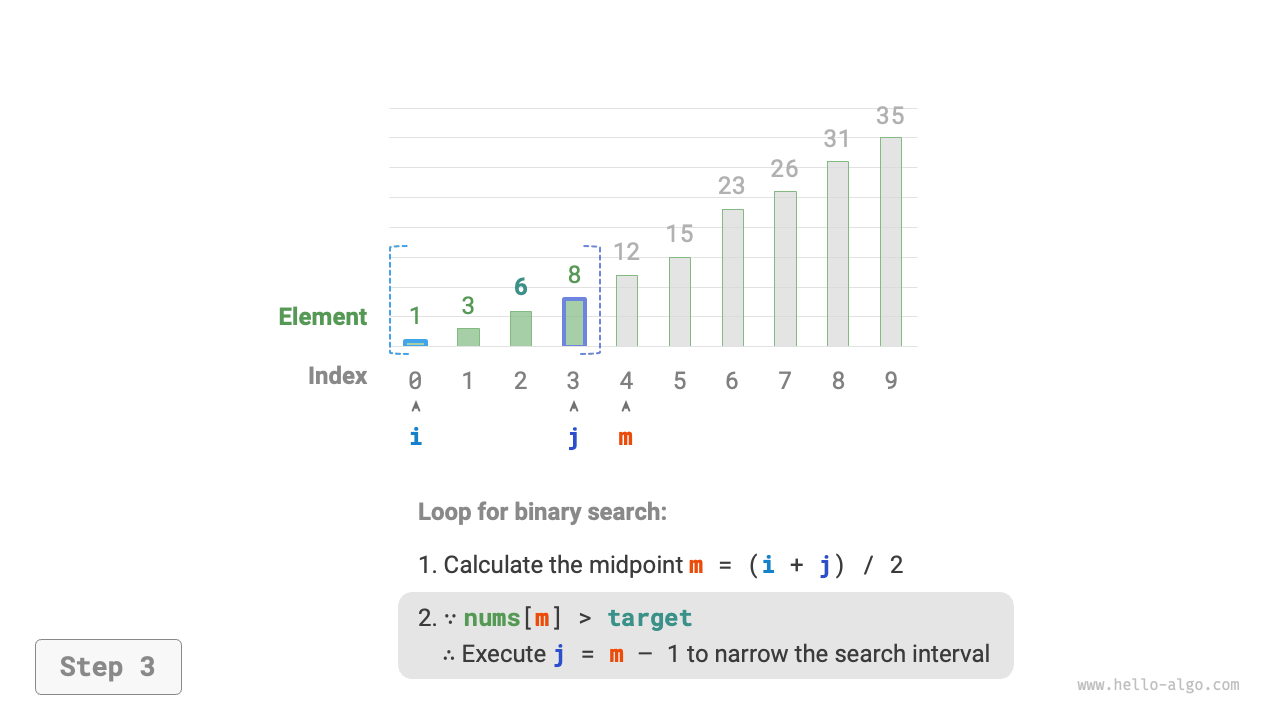
    2. If nums[m] > target, it indicates that target is in the interval \([i, m - 1]\), thus set \(j = m - 1\).
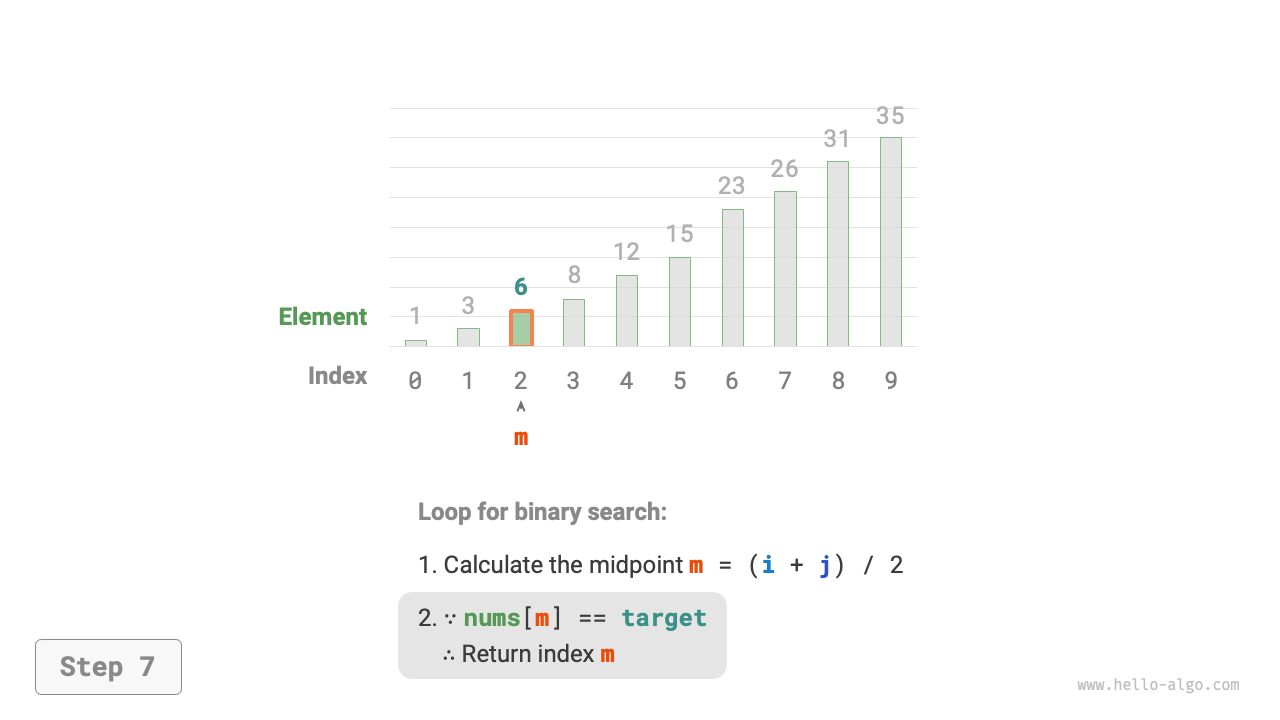
    3. If nums[m] = target, it indicates that target is found, thus return index \(m\).

If the array does not contain the target element, the search interval will eventually reduce to empty. In this case, return \(-1\).

Binary search process

binary_search_step2

binary_search_step3

binary_search_step4

binary_search_step5

binary_search_step6

binary_search_step7

Figure 10-2   Binary search process

It's worth noting that since \(i\) and \(j\) are both of type int, \(i + j\) might exceed the range of int type. To avoid large number overflow, we usually use the formula \(m = \lfloor {i + (j - i) / 2} \rfloor\) to calculate the midpoint.

The code is as follows:

binary_search.py
def binary_search(nums: list[int], target: int) -> int:
    """二分查找（双闭区间）"""
    # 初始化双闭区间 [0, n-1] ，即 i, j 分别指向数组首元素、尾元素
    i, j = 0, len(nums) - 1
    # 循环，当搜索区间为空时跳出（当 i > j 时为空）
    while i <= j:
        # 理论上 Python 的数字可以无限大（取决于内存大小），无须考虑大数越界问题
        m = (i + j) // 2  # 计算中点索引 m
        if nums[m] < target:
            i = m + 1  # 此情况说明 target 在区间 [m+1, j] 中
        elif nums[m] > target:
            j = m - 1  # 此情况说明 target 在区间 [i, m-1] 中
        else:
            return m  # 找到目标元素，返回其索引
    return -1  # 未找到目标元素，返回 -1
binary_search.cpp
/* 二分查找（双闭区间） */
int binarySearch(vector<int> &nums, int target) {
    // 初始化双闭区间 [0, n-1] ，即 i, j 分别指向数组首元素、尾元素
    int i = 0, j = nums.size() - 1;
    // 循环，当搜索区间为空时跳出（当 i > j 时为空）
    while (i <= j) {
        int m = i + (j - i) / 2; // 计算中点索引 m
        if (nums[m] < target)    // 此情况说明 target 在区间 [m+1, j] 中
            i = m + 1;
        else if (nums[m] > target) // 此情况说明 target 在区间 [i, m-1] 中
            j = m - 1;
        else // 找到目标元素，返回其索引
            return m;
    }
    // 未找到目标元素，返回 -1
    return -1;
}
binary_search.java
/* 二分查找（双闭区间） */
int binarySearch(int[] nums, int target) {
    // 初始化双闭区间 [0, n-1] ，即 i, j 分别指向数组首元素、尾元素
    int i = 0, j = nums.length - 1;
    // 循环，当搜索区间为空时跳出（当 i > j 时为空）
    while (i <= j) {
        int m = i + (j - i) / 2; // 计算中点索引 m
        if (nums[m] < target) // 此情况说明 target 在区间 [m+1, j] 中
            i = m + 1;
        else if (nums[m] > target) // 此情况说明 target 在区间 [i, m-1] 中
            j = m - 1;
        else // 找到目标元素，返回其索引
            return m;
    }
    // 未找到目标元素，返回 -1
    return -1;
}
binary_search.cs
/* 二分查找（双闭区间） */
int BinarySearch(int[] nums, int target) {
    // 初始化双闭区间 [0, n-1] ，即 i, j 分别指向数组首元素、尾元素
    int i = 0, j = nums.Length - 1;
    // 循环，当搜索区间为空时跳出（当 i > j 时为空）
    while (i <= j) {
        int m = i + (j - i) / 2;   // 计算中点索引 m
        if (nums[m] < target)      // 此情况说明 target 在区间 [m+1, j] 中
            i = m + 1;
        else if (nums[m] > target) // 此情况说明 target 在区间 [i, m-1] 中
            j = m - 1;
        else                       // 找到目标元素，返回其索引
            return m;
    }
    // 未找到目标元素，返回 -1
    return -1;
}
binary_search.go
/* 二分查找（双闭区间） */
func binarySearch(nums []int, target int) int {
    // 初始化双闭区间 [0, n-1] ，即 i, j 分别指向数组首元素、尾元素
    i, j := 0, len(nums)-1
    // 循环，当搜索区间为空时跳出（当 i > j 时为空）
    for i <= j {
        m := i + (j-i)/2      // 计算中点索引 m
        if nums[m] < target { // 此情况说明 target 在区间 [m+1, j] 中
            i = m + 1
        } else if nums[m] > target { // 此情况说明 target 在区间 [i, m-1] 中
            j = m - 1
        } else { // 找到目标元素，返回其索引
            return m
        }
    }
    // 未找到目标元素，返回 -1
    return -1
}
binary_search.swift
/* 二分查找（双闭区间） */
func binarySearch(nums: [Int], target: Int) -> Int {
    // 初始化双闭区间 [0, n-1] ，即 i, j 分别指向数组首元素、尾元素
    var i = nums.startIndex
    var j = nums.endIndex - 1
    // 循环，当搜索区间为空时跳出（当 i > j 时为空）
    while i <= j {
        let m = i + (j - i) / 2 // 计算中点索引 m
        if nums[m] < target { // 此情况说明 target 在区间 [m+1, j] 中
            i = m + 1
        } else if nums[m] > target { // 此情况说明 target 在区间 [i, m-1] 中
            j = m - 1
        } else { // 找到目标元素，返回其索引
            return m
        }
    }
    // 未找到目标元素，返回 -1
    return -1
}
binary_search.js
/* 二分查找（双闭区间） */
function binarySearch(nums, target) {
    // 初始化双闭区间 [0, n-1] ，即 i, j 分别指向数组首元素、尾元素
    let i = 0,
        j = nums.length - 1;
    // 循环，当搜索区间为空时跳出（当 i > j 时为空）
    while (i <= j) {
        // 计算中点索引 m ，使用 parseInt() 向下取整
        const m = parseInt(i + (j - i) / 2);
        if (nums[m] < target)
            // 此情况说明 target 在区间 [m+1, j] 中
            i = m + 1;
        else if (nums[m] > target)
            // 此情况说明 target 在区间 [i, m-1] 中
            j = m - 1;
        else return m; // 找到目标元素，返回其索引
    }
    // 未找到目标元素，返回 -1
    return -1;
}
binary_search.ts
/* 二分查找（双闭区间） */
function binarySearch(nums: number[], target: number): number {
    // 初始化双闭区间 [0, n-1] ，即 i, j 分别指向数组首元素、尾元素
    let i = 0,
        j = nums.length - 1;
    // 循环，当搜索区间为空时跳出（当 i > j 时为空）
    while (i <= j) {
        // 计算中点索引 m
        const m = Math.floor(i + (j - i) / 2);
        if (nums[m] < target) {
            // 此情况说明 target 在区间 [m+1, j] 中
            i = m + 1;
        } else if (nums[m] > target) {
            // 此情况说明 target 在区间 [i, m-1] 中
            j = m - 1;
        } else {
            // 找到目标元素，返回其索引
            return m;
        }
    }
    return -1; // 未找到目标元素，返回 -1
}
binary_search.dart
/* 二分查找（双闭区间） */
int binarySearch(List<int> nums, int target) {
  // 初始化双闭区间 [0, n-1] ，即 i, j 分别指向数组首元素、尾元素
  int i = 0, j = nums.length - 1;
  // 循环，当搜索区间为空时跳出（当 i > j 时为空）
  while (i <= j) {
    int m = i + (j - i) ~/ 2; // 计算中点索引 m
    if (nums[m] < target) {
      // 此情况说明 target 在区间 [m+1, j] 中
      i = m + 1;
    } else if (nums[m] > target) {
      // 此情况说明 target 在区间 [i, m-1] 中
      j = m - 1;
    } else {
      // 找到目标元素，返回其索引
      return m;
    }
  }
  // 未找到目标元素，返回 -1
  return -1;
}
binary_search.rs
/* 二分查找（双闭区间） */
fn binary_search(nums: &[i32], target: i32) -> i32 {
    // 初始化双闭区间 [0, n-1] ，即 i, j 分别指向数组首元素、尾元素
    let mut i = 0;
    let mut j = nums.len() as i32 - 1;
    // 循环，当搜索区间为空时跳出（当 i > j 时为空）
    while i <= j {
        let m = i + (j - i) / 2; // 计算中点索引 m
        if nums[m as usize] < target {
            // 此情况说明 target 在区间 [m+1, j] 中
            i = m + 1;
        } else if nums[m as usize] > target {
            // 此情况说明 target 在区间 [i, m-1] 中
            j = m - 1;
        } else {
            // 找到目标元素，返回其索引
            return m;
        }
    }
    // 未找到目标元素，返回 -1
    return -1;
}
binary_search.c
/* 二分查找（双闭区间） */
int binarySearch(int *nums, int len, int target) {
    // 初始化双闭区间 [0, n-1] ，即 i, j 分别指向数组首元素、尾元素
    int i = 0, j = len - 1;
    // 循环，当搜索区间为空时跳出（当 i > j 时为空）
    while (i <= j) {
        int m = i + (j - i) / 2; // 计算中点索引 m
        if (nums[m] < target)    // 此情况说明 target 在区间 [m+1, j] 中
            i = m + 1;
        else if (nums[m] > target) // 此情况说明 target 在区间 [i, m-1] 中
            j = m - 1;
        else // 找到目标元素，返回其索引
            return m;
    }
    // 未找到目标元素，返回 -1
    return -1;
}
binary_search.kt
/* 二分查找（双闭区间） */
fun binarySearch(nums: IntArray, target: Int): Int {
    // 初始化双闭区间 [0, n-1] ，即 i, j 分别指向数组首元素、尾元素
    var i = 0
    var j = nums.size - 1
    // 循环，当搜索区间为空时跳出（当 i > j 时为空）
    while (i <= j) {
        val m = i + (j - i) / 2 // 计算中点索引 m
        if (nums[m] < target) // 此情况说明 target 在区间 [m+1, j] 中
            i = m + 1
        else if (nums[m] > target) // 此情况说明 target 在区间 [i, m-1] 中
            j = m - 1
        else  // 找到目标元素，返回其索引
            return m
    }
    // 未找到目标元素，返回 -1
    return -1
}
binary_search.rb
### 二分查找（双闭区间） ###
def binary_search(nums, target)
  # 初始化双闭区间 [0, n-1] ，即 i, j 分别指向数组首元素、尾元素
  i, j = 0, nums.length - 1

  # 循环，当搜索区间为空时跳出（当 i > j 时为空）
  while i <= j
    # 理论上 Ruby 的数字可以无限大（取决于内存大小），无须考虑大数越界问题
    m = (i + j) / 2   # 计算中点索引 m

    if nums[m] < target
      i = m + 1 # 此情况说明 target 在区间 [m+1, j] 中
    elsif nums[m] > target
      j = m - 1 # 此情况说明 target 在区间 [i, m-1] 中
    else
      return m  # 找到目标元素，返回其索引
    end
  end

  -1  # 未找到目标元素，返回 -1
end
binary_search.zig
// 二分查找（双闭区间）
fn binarySearch(comptime T: type, nums: std.ArrayList(T), target: T) T {
    // 初始化双闭区间 [0, n-1] ，即 i, j 分别指向数组首元素、尾元素
    var i: usize = 0;
    var j: usize = nums.items.len - 1;
    // 循环，当搜索区间为空时跳出（当 i > j 时为空）
    while (i <= j) {
        var m = i + (j - i) / 2;                // 计算中点索引 m
        if (nums.items[m] < target) {           // 此情况说明 target 在区间 [m+1, j] 中
            i = m + 1;
        } else if (nums.items[m] > target) {    // 此情况说明 target 在区间 [i, m-1] 中
            j = m - 1;
        } else {                                // 找到目标元素，返回其索引
            return @intCast(m);
        }
    }
    // 未找到目标元素，返回 -1
    return -1;
}
Code Visualization

Time complexity is \(O(\log n)\) : In the binary loop, the interval reduces by half each round, hence the number of iterations is \(\log_2 n\).

Space complexity is \(O(1)\) : Pointers \(i\) and \(j\) use constant size space.

10.1.1   Interval representation methods

Besides the aforementioned closed interval, a common interval representation is the "left-closed right-open" interval, defined as \([0, n)\), where the left boundary includes itself, and the right boundary does not include itself. In this representation, the interval \([i, j)\) is empty when \(i = j\).

We can implement a binary search algorithm with the same functionality based on this representation:

binary_search.py
def binary_search_lcro(nums: list[int], target: int) -> int:
    """二分查找（左闭右开区间）"""
    # 初始化左闭右开区间 [0, n) ，即 i, j 分别指向数组首元素、尾元素+1
    i, j = 0, len(nums)
    # 循环，当搜索区间为空时跳出（当 i = j 时为空）
    while i < j:
        m = (i + j) // 2  # 计算中点索引 m
        if nums[m] < target:
            i = m + 1  # 此情况说明 target 在区间 [m+1, j) 中
        elif nums[m] > target:
            j = m  # 此情况说明 target 在区间 [i, m) 中
        else:
            return m  # 找到目标元素，返回其索引
    return -1  # 未找到目标元素，返回 -1
binary_search.cpp
/* 二分查找（左闭右开区间） */
int binarySearchLCRO(vector<int> &nums, int target) {
    // 初始化左闭右开区间 [0, n) ，即 i, j 分别指向数组首元素、尾元素+1
    int i = 0, j = nums.size();
    // 循环，当搜索区间为空时跳出（当 i = j 时为空）
    while (i < j) {
        int m = i + (j - i) / 2; // 计算中点索引 m
        if (nums[m] < target)    // 此情况说明 target 在区间 [m+1, j) 中
            i = m + 1;
        else if (nums[m] > target) // 此情况说明 target 在区间 [i, m) 中
            j = m;
        else // 找到目标元素，返回其索引
            return m;
    }
    // 未找到目标元素，返回 -1
    return -1;
}
binary_search.java
/* 二分查找（左闭右开区间） */
int binarySearchLCRO(int[] nums, int target) {
    // 初始化左闭右开区间 [0, n) ，即 i, j 分别指向数组首元素、尾元素+1
    int i = 0, j = nums.length;
    // 循环，当搜索区间为空时跳出（当 i = j 时为空）
    while (i < j) {
        int m = i + (j - i) / 2; // 计算中点索引 m
        if (nums[m] < target) // 此情况说明 target 在区间 [m+1, j) 中
            i = m + 1;
        else if (nums[m] > target) // 此情况说明 target 在区间 [i, m) 中
            j = m;
        else // 找到目标元素，返回其索引
            return m;
    }
    // 未找到目标元素，返回 -1
    return -1;
}
binary_search.cs
/* 二分查找（左闭右开区间） */
int BinarySearchLCRO(int[] nums, int target) {
    // 初始化左闭右开区间 [0, n) ，即 i, j 分别指向数组首元素、尾元素+1
    int i = 0, j = nums.Length;
    // 循环，当搜索区间为空时跳出（当 i = j 时为空）
    while (i < j) {
        int m = i + (j - i) / 2;   // 计算中点索引 m
        if (nums[m] < target)      // 此情况说明 target 在区间 [m+1, j) 中
            i = m + 1;
        else if (nums[m] > target) // 此情况说明 target 在区间 [i, m) 中
            j = m;
        else                       // 找到目标元素，返回其索引
            return m;
    }
    // 未找到目标元素，返回 -1
    return -1;
}
binary_search.go
/* 二分查找（左闭右开区间） */
func binarySearchLCRO(nums []int, target int) int {
    // 初始化左闭右开区间 [0, n) ，即 i, j 分别指向数组首元素、尾元素+1
    i, j := 0, len(nums)
    // 循环，当搜索区间为空时跳出（当 i = j 时为空）
    for i < j {
        m := i + (j-i)/2      // 计算中点索引 m
        if nums[m] < target { // 此情况说明 target 在区间 [m+1, j) 中
            i = m + 1
        } else if nums[m] > target { // 此情况说明 target 在区间 [i, m) 中
            j = m
        } else { // 找到目标元素，返回其索引
            return m
        }
    }
    // 未找到目标元素，返回 -1
    return -1
}
binary_search.swift
/* 二分查找（左闭右开区间） */
func binarySearchLCRO(nums: [Int], target: Int) -> Int {
    // 初始化左闭右开区间 [0, n) ，即 i, j 分别指向数组首元素、尾元素+1
    var i = nums.startIndex
    var j = nums.endIndex
    // 循环，当搜索区间为空时跳出（当 i = j 时为空）
    while i < j {
        let m = i + (j - i) / 2 // 计算中点索引 m
        if nums[m] < target { // 此情况说明 target 在区间 [m+1, j) 中
            i = m + 1
        } else if nums[m] > target { // 此情况说明 target 在区间 [i, m) 中
            j = m
        } else { // 找到目标元素，返回其索引
            return m
        }
    }
    // 未找到目标元素，返回 -1
    return -1
}
binary_search.js
/* 二分查找（左闭右开区间） */
function binarySearchLCRO(nums, target) {
    // 初始化左闭右开区间 [0, n) ，即 i, j 分别指向数组首元素、尾元素+1
    let i = 0,
        j = nums.length;
    // 循环，当搜索区间为空时跳出（当 i = j 时为空）
    while (i < j) {
        // 计算中点索引 m ，使用 parseInt() 向下取整
        const m = parseInt(i + (j - i) / 2);
        if (nums[m] < target)
            // 此情况说明 target 在区间 [m+1, j) 中
            i = m + 1;
        else if (nums[m] > target)
            // 此情况说明 target 在区间 [i, m) 中
            j = m;
        // 找到目标元素，返回其索引
        else return m;
    }
    // 未找到目标元素，返回 -1
    return -1;
}
binary_search.ts
/* 二分查找（左闭右开区间） */
function binarySearchLCRO(nums: number[], target: number): number {
    // 初始化左闭右开区间 [0, n) ，即 i, j 分别指向数组首元素、尾元素+1
    let i = 0,
        j = nums.length;
    // 循环，当搜索区间为空时跳出（当 i = j 时为空）
    while (i < j) {
        // 计算中点索引 m
        const m = Math.floor(i + (j - i) / 2);
        if (nums[m] < target) {
            // 此情况说明 target 在区间 [m+1, j) 中
            i = m + 1;
        } else if (nums[m] > target) {
            // 此情况说明 target 在区间 [i, m) 中
            j = m;
        } else {
            // 找到目标元素，返回其索引
            return m;
        }
    }
    return -1; // 未找到目标元素，返回 -1
}
binary_search.dart
/* 二分查找（左闭右开区间） */
int binarySearchLCRO(List<int> nums, int target) {
  // 初始化左闭右开区间 [0, n) ，即 i, j 分别指向数组首元素、尾元素+1
  int i = 0, j = nums.length;
  // 循环，当搜索区间为空时跳出（当 i = j 时为空）
  while (i < j) {
    int m = i + (j - i) ~/ 2; // 计算中点索引 m
    if (nums[m] < target) {
      // 此情况说明 target 在区间 [m+1, j) 中
      i = m + 1;
    } else if (nums[m] > target) {
      // 此情况说明 target 在区间 [i, m) 中
      j = m;
    } else {
      // 找到目标元素，返回其索引
      return m;
    }
  }
  // 未找到目标元素，返回 -1
  return -1;
}
binary_search.rs
/* 二分查找（左闭右开区间） */
fn binary_search_lcro(nums: &[i32], target: i32) -> i32 {
    // 初始化左闭右开区间 [0, n) ，即 i, j 分别指向数组首元素、尾元素+1
    let mut i = 0;
    let mut j = nums.len() as i32;
    // 循环，当搜索区间为空时跳出（当 i = j 时为空）
    while i < j {
        let m = i + (j - i) / 2; // 计算中点索引 m
        if nums[m as usize] < target {
            // 此情况说明 target 在区间 [m+1, j) 中
            i = m + 1;
        } else if nums[m as usize] > target {
            // 此情况说明 target 在区间 [i, m) 中
            j = m;
        } else {
            // 找到目标元素，返回其索引
            return m;
        }
    }
    // 未找到目标元素，返回 -1
    return -1;
}
binary_search.c
/* 二分查找（左闭右开区间） */
int binarySearchLCRO(int *nums, int len, int target) {
    // 初始化左闭右开区间 [0, n) ，即 i, j 分别指向数组首元素、尾元素+1
    int i = 0, j = len;
    // 循环，当搜索区间为空时跳出（当 i = j 时为空）
    while (i < j) {
        int m = i + (j - i) / 2; // 计算中点索引 m
        if (nums[m] < target)    // 此情况说明 target 在区间 [m+1, j) 中
            i = m + 1;
        else if (nums[m] > target) // 此情况说明 target 在区间 [i, m) 中
            j = m;
        else // 找到目标元素，返回其索引
            return m;
    }
    // 未找到目标元素，返回 -1
    return -1;
}
binary_search.kt
/* 二分查找（左闭右开区间） */
fun binarySearchLCRO(nums: IntArray, target: Int): Int {
    // 初始化左闭右开区间 [0, n) ，即 i, j 分别指向数组首元素、尾元素+1
    var i = 0
    var j = nums.size
    // 循环，当搜索区间为空时跳出（当 i = j 时为空）
    while (i < j) {
        val m = i + (j - i) / 2 // 计算中点索引 m
        if (nums[m] < target) // 此情况说明 target 在区间 [m+1, j) 中
            i = m + 1
        else if (nums[m] > target) // 此情况说明 target 在区间 [i, m) 中
            j = m
        else  // 找到目标元素，返回其索引
            return m
    }
    // 未找到目标元素，返回 -1
    return -1
}
binary_search.rb
### 二分查找（左闭右开区间） ###
def binary_search_lcro(nums, target)
  # 初始化左闭右开区间 [0, n) ，即 i, j 分别指向数组首元素、尾元素+1
  i, j = 0, nums.length

  # 循环，当搜索区间为空时跳出（当 i = j 时为空）
  while i < j
    # 计算中点索引 m
    m = (i + j) / 2

    if nums[m] < target
      i = m + 1 # 此情况说明 target 在区间 [m+1, j) 中
    elsif nums[m] > target
      j = m - 1 # 此情况说明 target 在区间 [i, m) 中
    else
      return m  # 找到目标元素，返回其索引
    end
  end

  -1  # 未找到目标元素，返回 -1
end
binary_search.zig
// 二分查找（左闭右开区间）
fn binarySearchLCRO(comptime T: type, nums: std.ArrayList(T), target: T) T {
    // 初始化左闭右开区间 [0, n) ，即 i, j 分别指向数组首元素、尾元素+1
    var i: usize = 0;
    var j: usize = nums.items.len;
    // 循环，当搜索区间为空时跳出（当 i = j 时为空）
    while (i <= j) {
        var m = i + (j - i) / 2;                // 计算中点索引 m
        if (nums.items[m] < target) {           // 此情况说明 target 在区间 [m+1, j) 中
            i = m + 1;
        } else if (nums.items[m] > target) {    // 此情况说明 target 在区间 [i, m) 中
            j = m;
        } else {                                // 找到目标元素，返回其索引
            return @intCast(m);
        }
    }
    // 未找到目标元素，返回 -1
    return -1;
}
Code Visualization

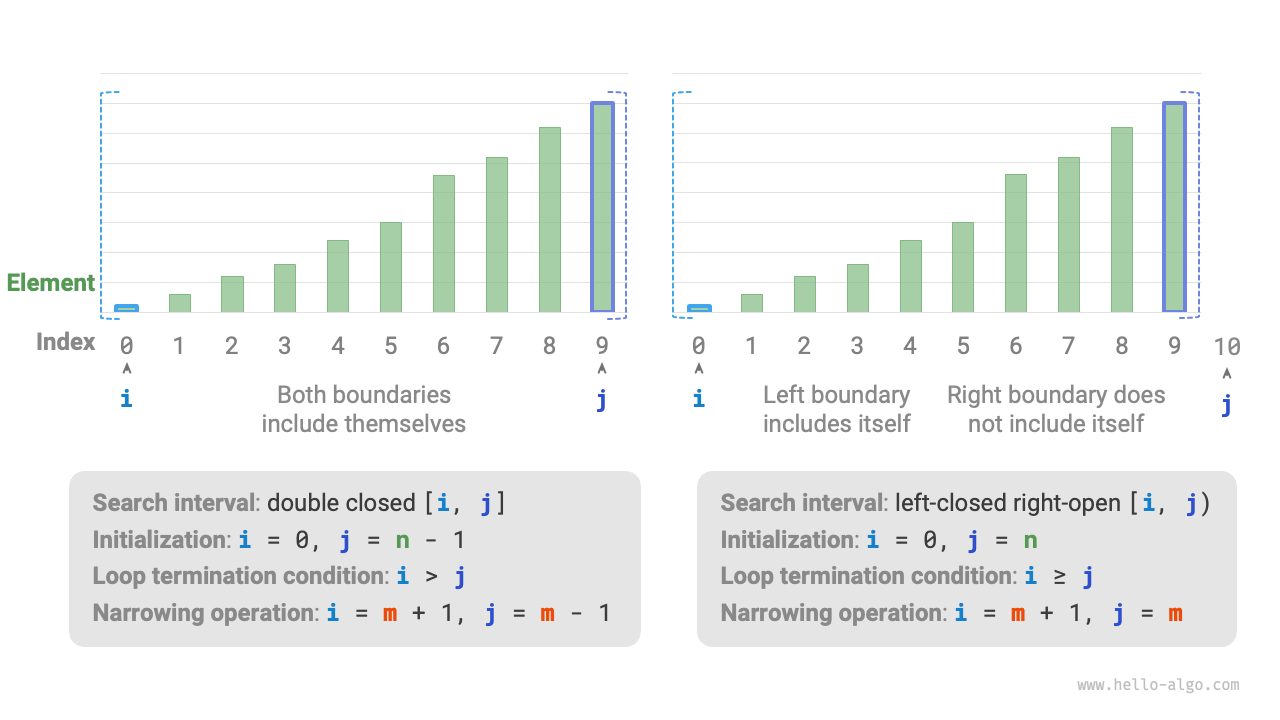
As shown in Figure 10-3, in the two types of interval representations, the initialization of the binary search algorithm, the loop condition, and the narrowing interval operation are different.

Since both boundaries in the "closed interval" representation are defined as closed, the operations to narrow the interval through pointers \(i\) and \(j\) are also symmetrical. This makes it less prone to errors, therefore, it is generally recommended to use the "closed interval" approach.

Two types of interval definitions

Figure 10-3   Two types of interval definitions

10.1.2   Advantages and limitations

Binary search performs well in both time and space aspects.

  • Binary search is time-efficient. With large data volumes, the logarithmic time complexity has a significant advantage. For instance, when the data size \(n = 2^{20}\), linear search requires \(2^{20} = 1048576\) iterations, while binary search only requires \(\log_2 2^{20} = 20\) iterations.
  • Binary search does not require extra space. Compared to search algorithms that rely on additional space (like hash search), binary search is more space-efficient.

However, binary search is not suitable for all situations, mainly for the following reasons.

  • Binary search is only applicable to ordered data. If the input data is unordered, it is not worth sorting it just to use binary search, as sorting algorithms typically have a time complexity of \(O(n \log n)\), which is higher than both linear and binary search. For scenarios with frequent element insertion to maintain array order, inserting elements into specific positions has a time complexity of \(O(n)\), which is also quite costly.
  • Binary search is only applicable to arrays. Binary search requires non-continuous (jumping) element access, which is inefficient in linked lists, thus not suitable for use in linked lists or data structures based on linked lists.
  • With small data volumes, linear search performs better. In linear search, each round only requires 1 decision operation; whereas in binary search, it involves 1 addition, 1 division, 1 to 3 decision operations, 1 addition (subtraction), totaling 4 to 6 operations; therefore, when data volume \(n\) is small, linear search can be faster than binary search.
Feel free to drop your insights, questions or suggestions