7.1 二元樹¶

二元樹（binary tree）是一種非線性資料結構，代表“祖先”與“後代”之間的派生關係，體現了“一分為二”的分治邏輯。與鏈結串列類似，二元樹的基本單元是節點，每個節點包含值、左子節點引用和右子節點引用。

PythonC++JavaC#GoSwiftJSTSDartRustCKotlinRubyZig

class TreeNode:
    """二元樹節點類別"""
    def __init__(self, val: int):
        self.val: int = val                # 節點值
        self.left: TreeNode | None = None  # 左子節點引用
        self.right: TreeNode | None = None # 右子節點引用

/* 二元樹節點結構體 */
struct TreeNode {
    int val;          // 節點值
    TreeNode *left;   // 左子節點指標
    TreeNode *right;  // 右子節點指標
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};

/* 二元樹節點類別 */
class TreeNode {
    int val;         // 節點值
    TreeNode left;   // 左子節點引用
    TreeNode right;  // 右子節點引用
    TreeNode(int x) { val = x; }
}

/* 二元樹節點類別 */
class TreeNode(int? x) {
    public int? val = x;    // 節點值
    public TreeNode? left;  // 左子節點引用
    public TreeNode? right; // 右子節點引用
}

/* 二元樹節點結構體 */
type TreeNode struct {
    Val   int
    Left  *TreeNode
    Right *TreeNode
}
/* 建構子 */
func NewTreeNode(v int) *TreeNode {
    return &TreeNode{
        Left:  nil, // 左子節點指標
        Right: nil, // 右子節點指標
        Val:   v,   // 節點值
    }
}

/* 二元樹節點類別 */
class TreeNode {
    var val: Int // 節點值
    var left: TreeNode? // 左子節點引用
    var right: TreeNode? // 右子節點引用

    init(x: Int) {
        val = x
    }
}

/* 二元樹節點類別 */
class TreeNode {
    val; // 節點值
    left; // 左子節點指標
    right; // 右子節點指標
    constructor(val, left, right) {
        this.val = val === undefined ? 0 : val;
        this.left = left === undefined ? null : left;
        this.right = right === undefined ? null : right;
    }
}

/* 二元樹節點類別 */
class TreeNode {
    val: number;
    left: TreeNode | null;
    right: TreeNode | null;

    constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
        this.val = val === undefined ? 0 : val; // 節點值
        this.left = left === undefined ? null : left; // 左子節點引用
        this.right = right === undefined ? null : right; // 右子節點引用
    }
}

/* 二元樹節點類別 */
class TreeNode {
  int val;         // 節點值
  TreeNode? left;  // 左子節點引用
  TreeNode? right; // 右子節點引用
  TreeNode(this.val, [this.left, this.right]);
}

use std::rc::Rc;
use std::cell::RefCell;

/* 二元樹節點結構體 */
struct TreeNode {
    val: i32,                               // 節點值
    left: Option<Rc<RefCell<TreeNode>>>,    // 左子節點引用
    right: Option<Rc<RefCell<TreeNode>>>,   // 右子節點引用
}

impl TreeNode {
    /* 建構子 */
    fn new(val: i32) -> Rc<RefCell<Self>> {
        Rc::new(RefCell::new(Self {
            val,
            left: None,
            right: None
        }))
    }
}

/* 二元樹節點結構體 */
typedef struct TreeNode {
    int val;                // 節點值
    int height;             // 節點高度
    struct TreeNode *left;  // 左子節點指標
    struct TreeNode *right; // 右子節點指標
} TreeNode;

/* 建構子 */
TreeNode *newTreeNode(int val) {
    TreeNode *node;

    node = (TreeNode *)malloc(sizeof(TreeNode));
    node->val = val;
    node->height = 0;
    node->left = NULL;
    node->right = NULL;
    return node;
}

/* 二元樹節點類別 */
class TreeNode(val _val: Int) {  // 節點值
    val left: TreeNode? = null   // 左子節點引用
    val right: TreeNode? = null  // 右子節點引用
}

### 二元樹節點類別 ###
class TreeNode
  attr_accessor :val    # 節點值
  attr_accessor :left   # 左子節點引用
  attr_accessor :right  # 右子節點引用

  def initialize(val)
    @val = val
  end
end

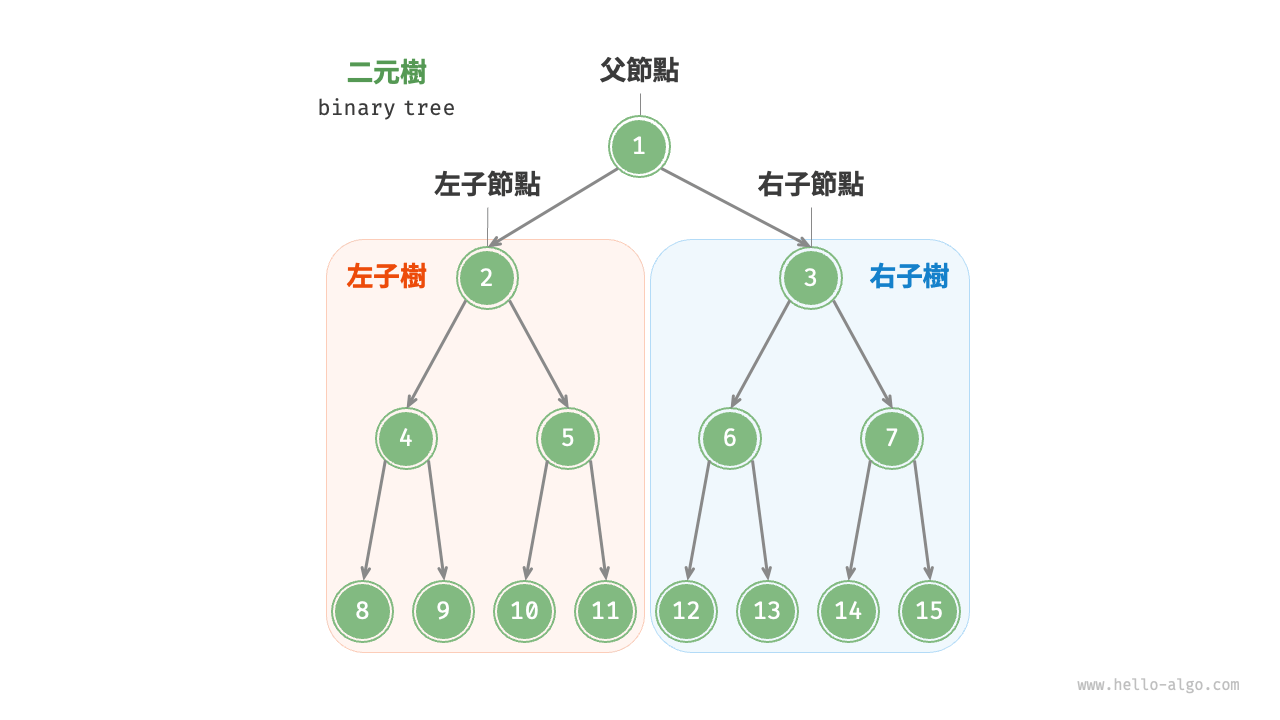
每個節點都有兩個引用（指標），分別指向左子節點（left-child node）和右子節點（right-child node），該節點被稱為這兩個子節點的父節點（parent node）。當給定一個二元樹的節點時，我們將該節點的左子節點及其以下節點形成的樹稱為該節點的左子樹（left subtree），同理可得右子樹（right subtree）。

在二元樹中，除葉節點外，其他所有節點都包含子節點和非空子樹。如圖 7-1 所示，如果將“節點 2”視為父節點，則其左子節點和右子節點分別是“節點 4”和“節點 5”，左子樹是“節點 4 及其以下節點形成的樹”，右子樹是“節點 5 及其以下節點形成的樹”。

圖 7-1 父節點、子節點、子樹

7.1.1 二元樹常見術語¶

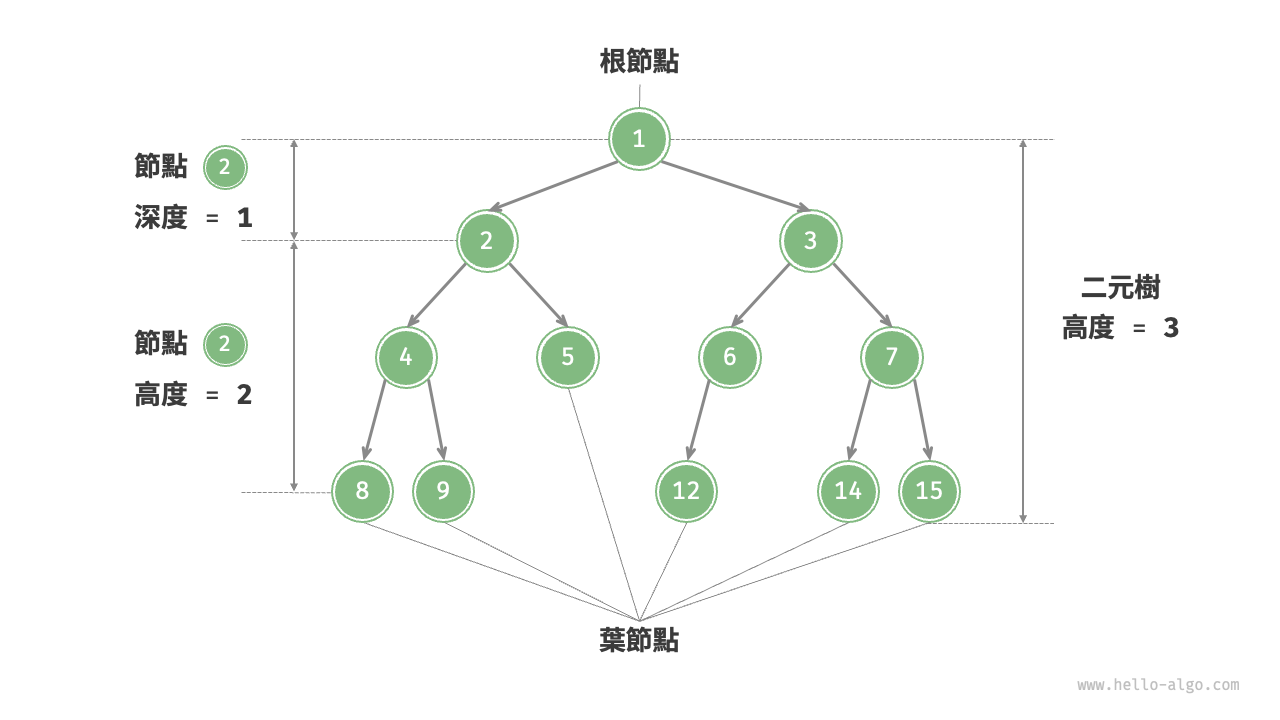
二元樹的常用術語如圖 7-2 所示。

根節點（root node）：位於二元樹頂層的節點，沒有父節點。
葉節點（leaf node）：沒有子節點的節點，其兩個指標均指向 None 。
邊（edge）：連線兩個節點的線段，即節點引用（指標）。
節點所在的層（level）：從頂至底遞增，根節點所在層為 1 。
節點的度（degree）：節點的子節點的數量。在二元樹中，度的取值範圍是 0、1、2 。
二元樹的高度（height）：從根節點到最遠葉節點所經過的邊的數量。
節點的深度（depth）：從根節點到該節點所經過的邊的數量。
節點的高度（height）：從距離該節點最遠的葉節點到該節點所經過的邊的數量。

圖 7-2 二元樹的常用術語

Tip

請注意，我們通常將“高度”和“深度”定義為“經過的邊的數量”，但有些題目或教材可能會將其定義為“經過的節點的數量”。在這種情況下，高度和深度都需要加 1 。

7.1.2 二元樹基本操作¶

1. 初始化二元樹¶

與鏈結串列類似，首先初始化節點，然後構建引用（指標）。

PythonC++JavaC#GoSwiftJSTSDartRustCKotlinRubyZig

binary_tree.py

# 初始化二元樹
# 初始化節點
n1 = TreeNode(val=1)
n2 = TreeNode(val=2)
n3 = TreeNode(val=3)
n4 = TreeNode(val=4)
n5 = TreeNode(val=5)
# 構建節點之間的引用（指標）
n1.left = n2
n1.right = n3
n2.left = n4
n2.right = n5

binary_tree.cpp

/* 初始化二元樹 */
// 初始化節點
TreeNode* n1 = new TreeNode(1);
TreeNode* n2 = new TreeNode(2);
TreeNode* n3 = new TreeNode(3);
TreeNode* n4 = new TreeNode(4);
TreeNode* n5 = new TreeNode(5);
// 構建節點之間的引用（指標）
n1->left = n2;
n1->right = n3;
n2->left = n4;
n2->right = n5;

binary_tree.java

// 初始化節點
TreeNode n1 = new TreeNode(1);
TreeNode n2 = new TreeNode(2);
TreeNode n3 = new TreeNode(3);
TreeNode n4 = new TreeNode(4);
TreeNode n5 = new TreeNode(5);
// 構建節點之間的引用（指標）
n1.left = n2;
n1.right = n3;
n2.left = n4;
n2.right = n5;

binary_tree.cs

/* 初始化二元樹 */
// 初始化節點
TreeNode n1 = new(1);
TreeNode n2 = new(2);
TreeNode n3 = new(3);
TreeNode n4 = new(4);
TreeNode n5 = new(5);
// 構建節點之間的引用（指標）
n1.left = n2;
n1.right = n3;
n2.left = n4;
n2.right = n5;

binary_tree.go

/* 初始化二元樹 */
// 初始化節點
n1 := NewTreeNode(1)
n2 := NewTreeNode(2)
n3 := NewTreeNode(3)
n4 := NewTreeNode(4)
n5 := NewTreeNode(5)
// 構建節點之間的引用（指標）
n1.Left = n2
n1.Right = n3
n2.Left = n4
n2.Right = n5

binary_tree.swift

// 初始化節點
let n1 = TreeNode(x: 1)
let n2 = TreeNode(x: 2)
let n3 = TreeNode(x: 3)
let n4 = TreeNode(x: 4)
let n5 = TreeNode(x: 5)
// 構建節點之間的引用（指標）
n1.left = n2
n1.right = n3
n2.left = n4
n2.right = n5

binary_tree.js

/* 初始化二元樹 */
// 初始化節點
let n1 = new TreeNode(1),
    n2 = new TreeNode(2),
    n3 = new TreeNode(3),
    n4 = new TreeNode(4),
    n5 = new TreeNode(5);
// 構建節點之間的引用（指標）
n1.left = n2;
n1.right = n3;
n2.left = n4;
n2.right = n5;

binary_tree.ts

/* 初始化二元樹 */
// 初始化節點
let n1 = new TreeNode(1),
    n2 = new TreeNode(2),
    n3 = new TreeNode(3),
    n4 = new TreeNode(4),
    n5 = new TreeNode(5);
// 構建節點之間的引用（指標）
n1.left = n2;
n1.right = n3;
n2.left = n4;
n2.right = n5;

binary_tree.dart

/* 初始化二元樹 */
// 初始化節點
TreeNode n1 = new TreeNode(1);
TreeNode n2 = new TreeNode(2);
TreeNode n3 = new TreeNode(3);
TreeNode n4 = new TreeNode(4);
TreeNode n5 = new TreeNode(5);
// 構建節點之間的引用（指標）
n1.left = n2;
n1.right = n3;
n2.left = n4;
n2.right = n5;

binary_tree.rs

// 初始化節點
let n1 = TreeNode::new(1);
let n2 = TreeNode::new(2);
let n3 = TreeNode::new(3);
let n4 = TreeNode::new(4);
let n5 = TreeNode::new(5);
// 構建節點之間的引用（指標）
n1.borrow_mut().left = Some(n2.clone());
n1.borrow_mut().right = Some(n3);
n2.borrow_mut().left = Some(n4);
n2.borrow_mut().right = Some(n5);

binary_tree.c

/* 初始化二元樹 */
// 初始化節點
TreeNode *n1 = newTreeNode(1);
TreeNode *n2 = newTreeNode(2);
TreeNode *n3 = newTreeNode(3);
TreeNode *n4 = newTreeNode(4);
TreeNode *n5 = newTreeNode(5);
// 構建節點之間的引用（指標）
n1->left = n2;
n1->right = n3;
n2->left = n4;
n2->right = n5;

binary_tree.kt

// 初始化節點
val n1 = TreeNode(1)
val n2 = TreeNode(2)
val n3 = TreeNode(3)
val n4 = TreeNode(4)
val n5 = TreeNode(5)
// 構建節點之間的引用（指標）
n1.left = n2
n1.right = n3
n2.left = n4
n2.right = n5

binary_tree.rb

# 初始化二元樹
# 初始化節點
n1 = TreeNode.new(1)
n2 = TreeNode.new(2)
n3 = TreeNode.new(3)
n4 = TreeNode.new(4)
n5 = TreeNode.new(5)
# 構建節點之間的引用（指標）
n1.left = n2
n1.right = n3
n2.left = n4
n2.right = n5

binary_tree.zig

視覺化執行

全螢幕觀看 >

2. 插入與刪除節點¶

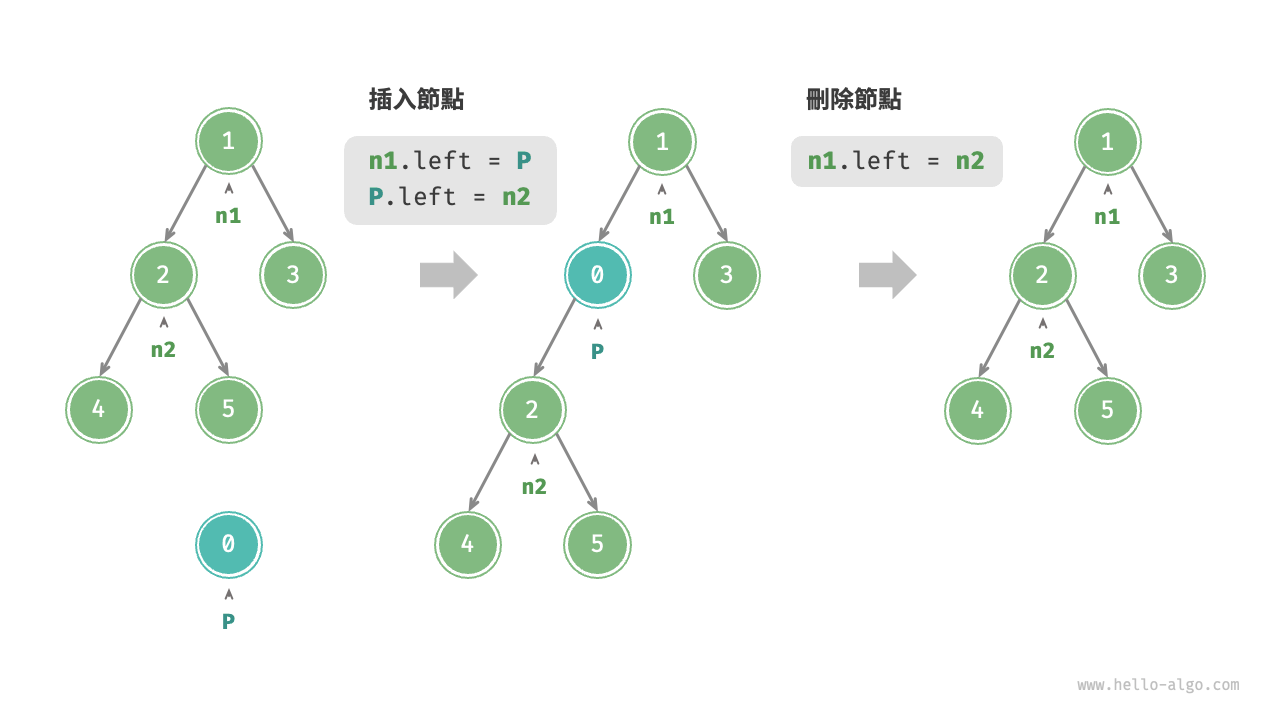
與鏈結串列類似，在二元樹中插入與刪除節點可以透過修改指標來實現。圖 7-3 給出了一個示例。

圖 7-3 在二元樹中插入與刪除節點

PythonC++JavaC#GoSwiftJSTSDartRustCKotlinRubyZig

binary_tree.py

# 插入與刪除節點
p = TreeNode(0)
# 在 n1 -> n2 中間插入節點 P
n1.left = p
p.left = n2
# 刪除節點 P
n1.left = n2

binary_tree.cpp

/* 插入與刪除節點 */
TreeNode* P = new TreeNode(0);
// 在 n1 -> n2 中間插入節點 P
n1->left = P;
P->left = n2;
// 刪除節點 P
n1->left = n2;

binary_tree.java

TreeNode P = new TreeNode(0);
// 在 n1 -> n2 中間插入節點 P
n1.left = P;
P.left = n2;
// 刪除節點 P
n1.left = n2;

binary_tree.cs

/* 插入與刪除節點 */
TreeNode P = new(0);
// 在 n1 -> n2 中間插入節點 P
n1.left = P;
P.left = n2;
// 刪除節點 P
n1.left = n2;

binary_tree.go

/* 插入與刪除節點 */
// 在 n1 -> n2 中間插入節點 P
p := NewTreeNode(0)
n1.Left = p
p.Left = n2
// 刪除節點 P
n1.Left = n2

binary_tree.swift

let P = TreeNode(x: 0)
// 在 n1 -> n2 中間插入節點 P
n1.left = P
P.left = n2
// 刪除節點 P
n1.left = n2

binary_tree.js

/* 插入與刪除節點 */
let P = new TreeNode(0);
// 在 n1 -> n2 中間插入節點 P
n1.left = P;
P.left = n2;
// 刪除節點 P
n1.left = n2;

binary_tree.ts

/* 插入與刪除節點 */
const P = new TreeNode(0);
// 在 n1 -> n2 中間插入節點 P
n1.left = P;
P.left = n2;
// 刪除節點 P
n1.left = n2;

binary_tree.dart

/* 插入與刪除節點 */
TreeNode P = new TreeNode(0);
// 在 n1 -> n2 中間插入節點 P
n1.left = P;
P.left = n2;
// 刪除節點 P
n1.left = n2;

binary_tree.rs

let p = TreeNode::new(0);
// 在 n1 -> n2 中間插入節點 P
n1.borrow_mut().left = Some(p.clone());
p.borrow_mut().left = Some(n2.clone());
// 刪除節點 p
n1.borrow_mut().left = Some(n2);

binary_tree.c

/* 插入與刪除節點 */
TreeNode *P = newTreeNode(0);
// 在 n1 -> n2 中間插入節點 P
n1->left = P;
P->left = n2;
// 刪除節點 P
n1->left = n2;

binary_tree.kt

val P = TreeNode(0)
// 在 n1 -> n2 中間插入節點 P
n1.left = P
P.left = n2
// 刪除節點 P
n1.left = n2

binary_tree.rb

# 插入與刪除節點
_p = TreeNode.new(0)
# 在 n1 -> n2 中間插入節點 _p
n1.left = _p
_p.left = n2
# 刪除節點
n1.left = n2

binary_tree.zig

視覺化執行

全螢幕觀看 >

Tip

需要注意的是，插入節點可能會改變二元樹的原有邏輯結構，而刪除節點通常意味著刪除該節點及其所有子樹。因此，在二元樹中，插入與刪除通常是由一套操作配合完成的，以實現有實際意義的操作。

7.1.3 常見二元樹型別¶

1. 完美二元樹¶

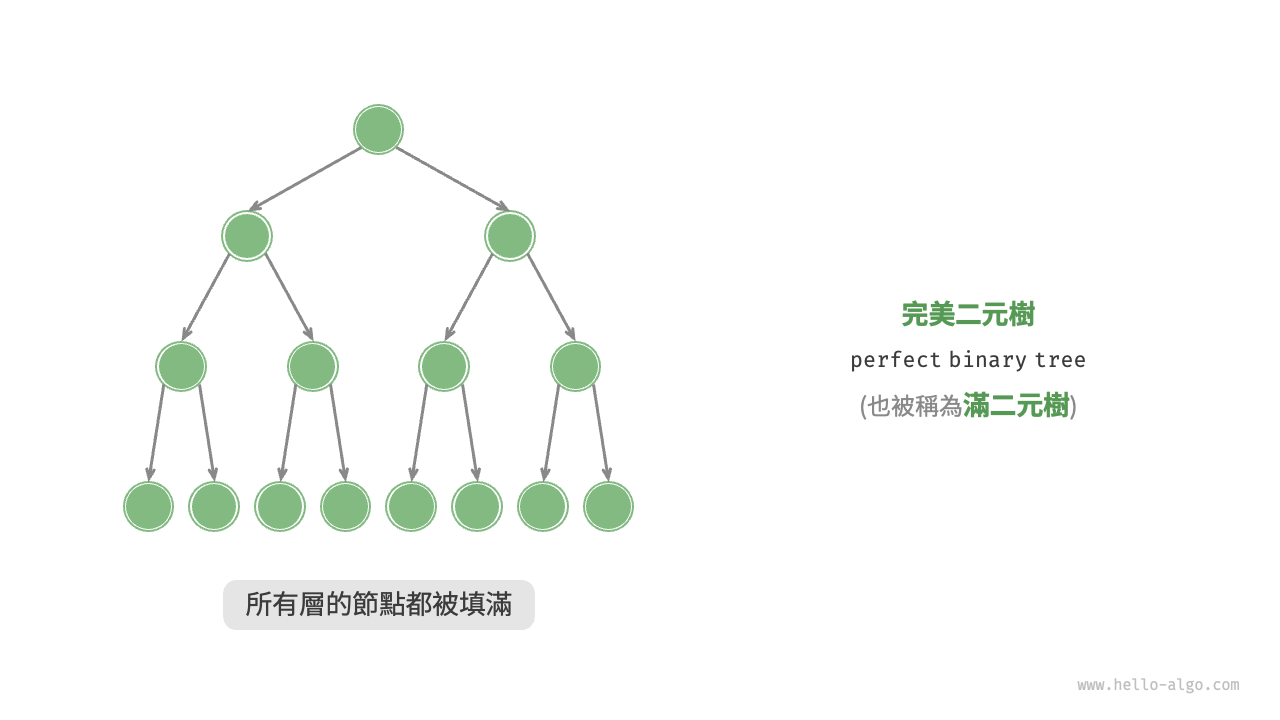
如圖 7-4 所示，完美二元樹（perfect binary tree）所有層的節點都被完全填滿。在完美二元樹中，葉節點的度為 \(0\) ，其餘所有節點的度都為 \(2\) ；若樹的高度為 \(h\) ，則節點總數為 \(2^{h+1} - 1\) ，呈現標準的指數級關係，反映了自然界中常見的細胞分裂現象。

Tip

請注意，在中文社群中，完美二元樹常被稱為滿二元樹。

圖 7-4 完美二元樹

2. 完全二元樹¶

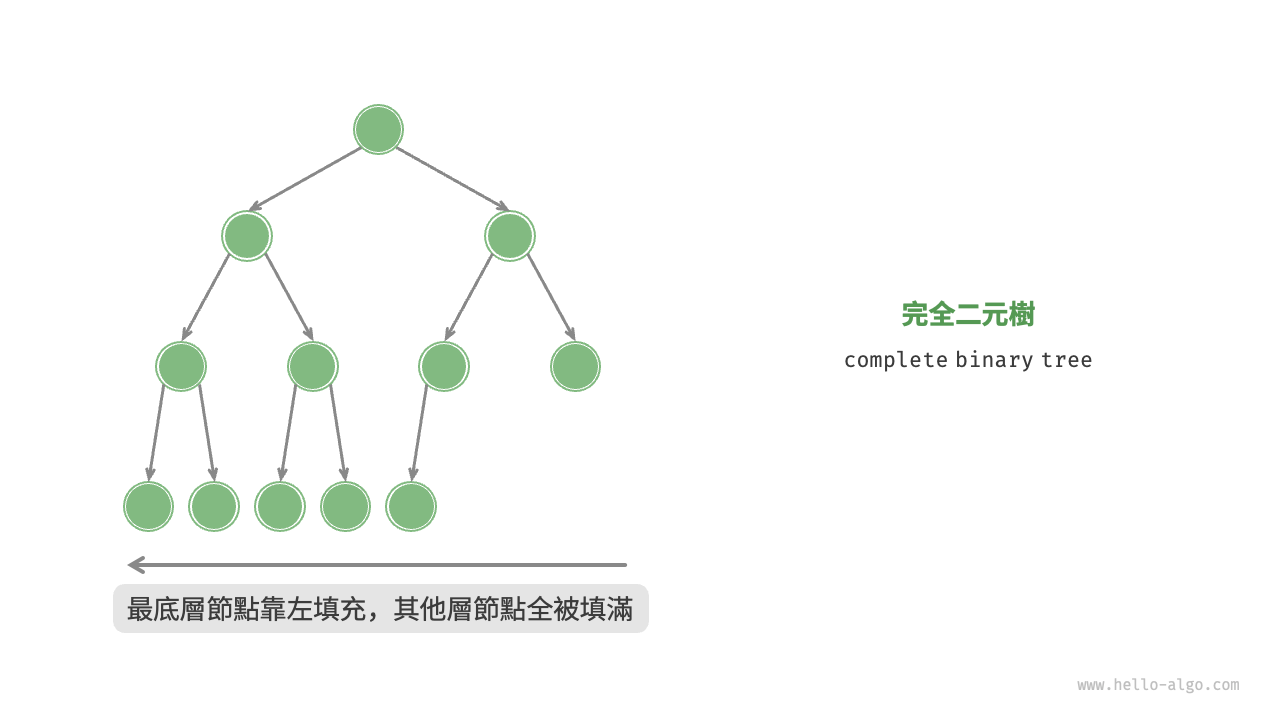
如圖 7-5 所示，完全二元樹（complete binary tree）只有最底層的節點未被填滿，且最底層節點儘量靠左填充。

圖 7-5 完全二元樹

3. 完滿二元樹¶

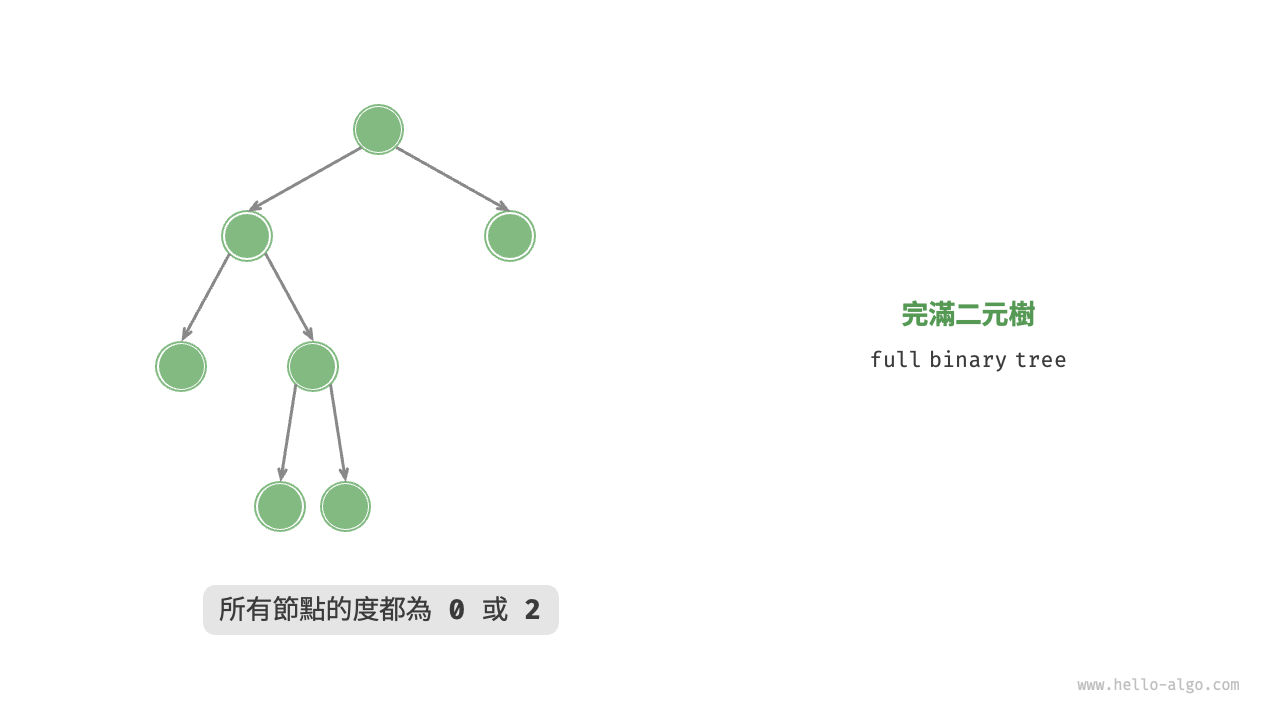
如圖 7-6 所示，完滿二元樹（full binary tree）除了葉節點之外，其餘所有節點都有兩個子節點。

圖 7-6 完滿二元樹

4. 平衡二元樹¶

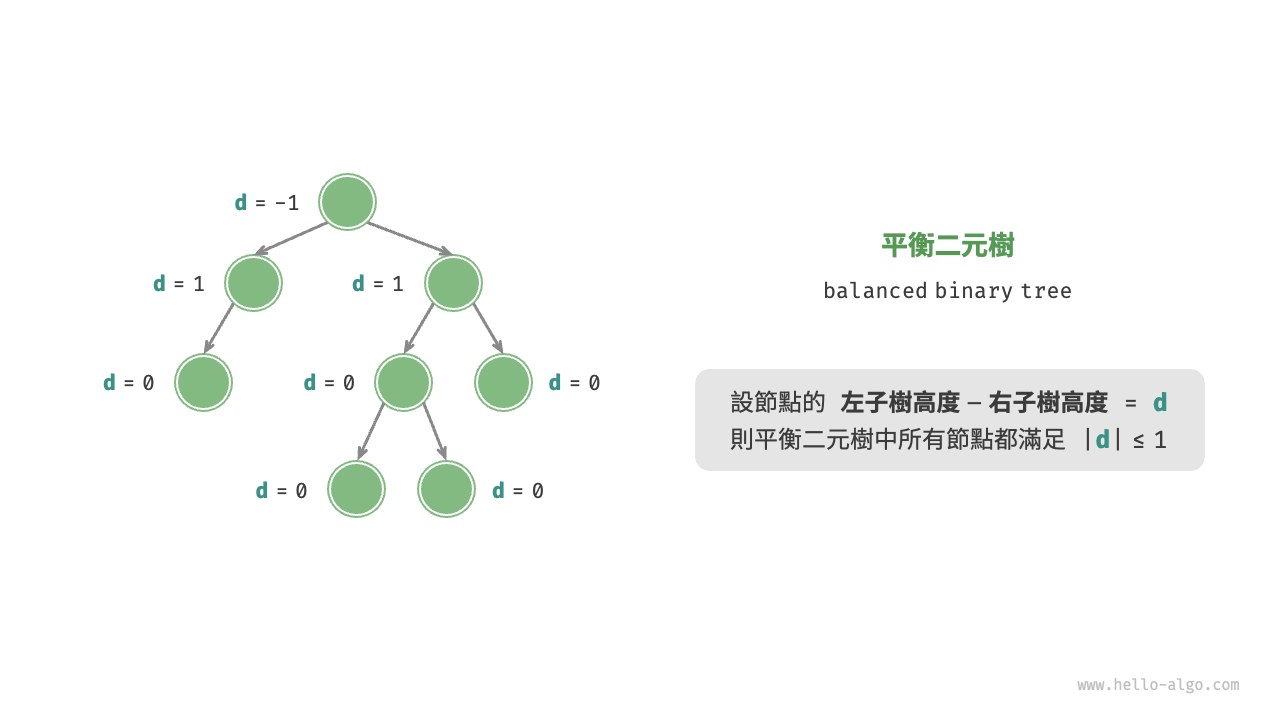
如圖 7-7 所示，平衡二元樹（balanced binary tree）中任意節點的左子樹和右子樹的高度之差的絕對值不超過 1 。

圖 7-7 平衡二元樹

7.1.4 二元樹的退化¶

圖 7-8 展示了二元樹的理想結構與退化結構。當二元樹的每層節點都被填滿時，達到“完美二元樹”；而當所有節點都偏向一側時，二元樹退化為“鏈結串列”。

完美二元樹是理想情況，可以充分發揮二元樹“分治”的優勢。
鏈結串列則是另一個極端，各項操作都變為線性操作，時間複雜度退化至 \(O(n)\) 。

圖 7-8 二元樹的最佳結構與最差結構

如表 7-1 所示，在最佳結構和最差結構下，二元樹的葉節點數量、節點總數、高度等達到極大值或極小值。

表 7-1 二元樹的最佳結構與最差結構

	完美二元樹	鏈結串列
第 \(i\) 層的節點數量	\(2^{i-1}\)	\(1\)
高度為 \(h\) 的樹的葉節點數量	\(2^h\)	\(1\)
高度為 \(h\) 的樹的節點總數	\(2^{h+1} - 1\)	\(h + 1\)
節點總數為 \(n\) 的樹的高度	\(\log_2 (n+1) - 1\)	\(n - 1\)