8.2 建堆操作
在某些情况下,我们希望使用一个列表的所有元素来构建一个堆,这个过程被称为“建堆操作”。
8.2.1 自上而下构建
我们首先创建一个空堆,然后遍历列表,依次对每个元素执行“入堆操作”,即先将元素添加至堆的尾部,再对该元素执行“从底至顶”堆化。
每当一个元素入堆,堆的长度就加一,因此堆是“自上而下”地构建的。
设元素数量为 \(n\) ,每个元素的入堆操作使用 \(O(\log{n})\) 时间,因此该建堆方法的时间复杂度为 \(O(n \log n)\) 。
8.2.2 自下而上构建
实际上,我们可以实现一种更为高效的建堆方法,共分为两步。
- 将列表所有元素原封不动添加到堆中。
- 倒序遍历堆(即层序遍历的倒序),依次对每个非叶节点执行“从顶至底堆化”。
在倒序遍历中,堆是“自下而上”地构建的,需要重点理解以下两点。
- 由于叶节点没有子节点,因此无需对它们执行堆化。最后一个节点的父节点是最后一个非叶节点。
- 在倒序遍历中,我们能够保证当前节点之下的子树已经完成堆化(已经是合法的堆),而这是堆化当前节点的前置条件。
my_heap.java/* 构造方法,根据输入列表建堆 */
MaxHeap(List<Integer> nums) {
// 将列表元素原封不动添加进堆
maxHeap = new ArrayList<>(nums);
// 堆化除叶节点以外的其他所有节点
for (int i = parent(size() - 1); i >= 0; i--) {
siftDown(i);
}
}
my_heap.cpp/* 构造方法,根据输入列表建堆 */
MaxHeap(vector<int> nums) {
// 将列表元素原封不动添加进堆
maxHeap = nums;
// 堆化除叶节点以外的其他所有节点
for (int i = parent(size() - 1); i >= 0; i--) {
siftDown(i);
}
}
my_heap.pydef __init__(self, nums: list[int]):
"""构造方法,根据输入列表建堆"""
# 将列表元素原封不动添加进堆
self.max_heap = nums
# 堆化除叶节点以外的其他所有节点
for i in range(self.parent(self.size() - 1), -1, -1):
self.sift_down(i)
my_heap.go/* 构造函数,根据切片建堆 */
func newMaxHeap(nums []any) *maxHeap {
// 将列表元素原封不动添加进堆
h := &maxHeap{data: nums}
for i := h.parent(len(h.data) - 1); i >= 0; i-- {
// 堆化除叶节点以外的其他所有节点
h.siftDown(i)
}
return h
}
my_heap.js/* 构造方法,建立空堆或根据输入列表建堆 */
constructor(nums) {
// 将列表元素原封不动添加进堆
this.#maxHeap = nums === undefined ? [] : [...nums];
// 堆化除叶节点以外的其他所有节点
for (let i = this.#parent(this.size() - 1); i >= 0; i--) {
this.#siftDown(i);
}
}
my_heap.ts/* 构造方法,建立空堆或根据输入列表建堆 */
constructor(nums?: number[]) {
// 将列表元素原封不动添加进堆
this.maxHeap = nums === undefined ? [] : [...nums];
// 堆化除叶节点以外的其他所有节点
for (let i = this.parent(this.size() - 1); i >= 0; i--) {
this.siftDown(i);
}
}
my_heap.c/* 构造函数,根据切片建堆 */
maxHeap *newMaxHeap(int nums[], int size) {
// 所有元素入堆
maxHeap *h = (maxHeap *)malloc(sizeof(maxHeap));
h->size = size;
memcpy(h->data, nums, size * sizeof(int));
for (int i = parent(size - 1); i >= 0; i--) {
// 堆化除叶节点以外的其他所有节点
siftDown(h, i);
}
return h;
}
my_heap.cs/* 构造函数,根据输入列表建堆 */
MaxHeap(IEnumerable<int> nums) {
// 将列表元素原封不动添加进堆
maxHeap = new List<int>(nums);
// 堆化除叶节点以外的其他所有节点
var size = parent(this.size() - 1);
for (int i = size; i >= 0; i--) {
siftDown(i);
}
}
my_heap.swift/* 构造方法,根据输入列表建堆 */
init(nums: [Int]) {
// 将列表元素原封不动添加进堆
maxHeap = nums
// 堆化除叶节点以外的其他所有节点
for i in stride(from: parent(i: size() - 1), through: 0, by: -1) {
siftDown(i: i)
}
}
my_heap.zig// 构造方法,根据输入列表建堆
fn init(self: *Self, allocator: std.mem.Allocator, nums: []const T) !void {
if (self.max_heap != null) return;
self.max_heap = std.ArrayList(T).init(allocator);
// 将列表元素原封不动添加进堆
try self.max_heap.?.appendSlice(nums);
// 堆化除叶节点以外的其他所有节点
var i: usize = parent(self.size() - 1) + 1;
while (i > 0) : (i -= 1) {
try self.siftDown(i - 1);
}
}
my_heap.dart/* 构造方法,根据输入列表建堆 */
MaxHeap(List<int> nums) {
// 将列表元素原封不动添加进堆
_maxHeap = nums;
// 堆化除叶节点以外的其他所有节点
for (int i = _parent(size() - 1); i >= 0; i--) {
siftDown(i);
}
}
my_heap.rs/* 构造方法,根据输入列表建堆 */
fn new(nums: Vec<i32>) -> Self {
// 将列表元素原封不动添加进堆
let mut heap = MaxHeap { max_heap: nums };
// 堆化除叶节点以外的其他所有节点
for i in (0..=Self::parent(heap.size() - 1)).rev() {
heap.sift_down(i);
}
heap
}
8.2.3 复杂度分析
下面,我们来尝试推算第二种建堆方法的时间复杂度。
- 假设完全二叉树的节点数量为 \(n\) ,则叶节点数量为 \((n + 1) / 2\) ,其中 \(/\) 为向下整除。因此需要堆化的节点数量为 \((n - 1) / 2\) 。
- 在从顶至底堆化的过程中,每个节点最多堆化到叶节点,因此最大迭代次数为二叉树高度 \(\log n\) 。
将上述两者相乘,可得到建堆过程的时间复杂度为 \(O(n \log n)\) 。但这个估算结果并不准确,因为我们没有考虑到二叉树底层节点数量远多于顶层节点的性质。
接下来我们来进行更为准确的计算。为了减小计算难度,假设给定一个节点数量为 \(n\) ,高度为 \(h\) 的“完美二叉树”,该假设不会影响计算结果的正确性。
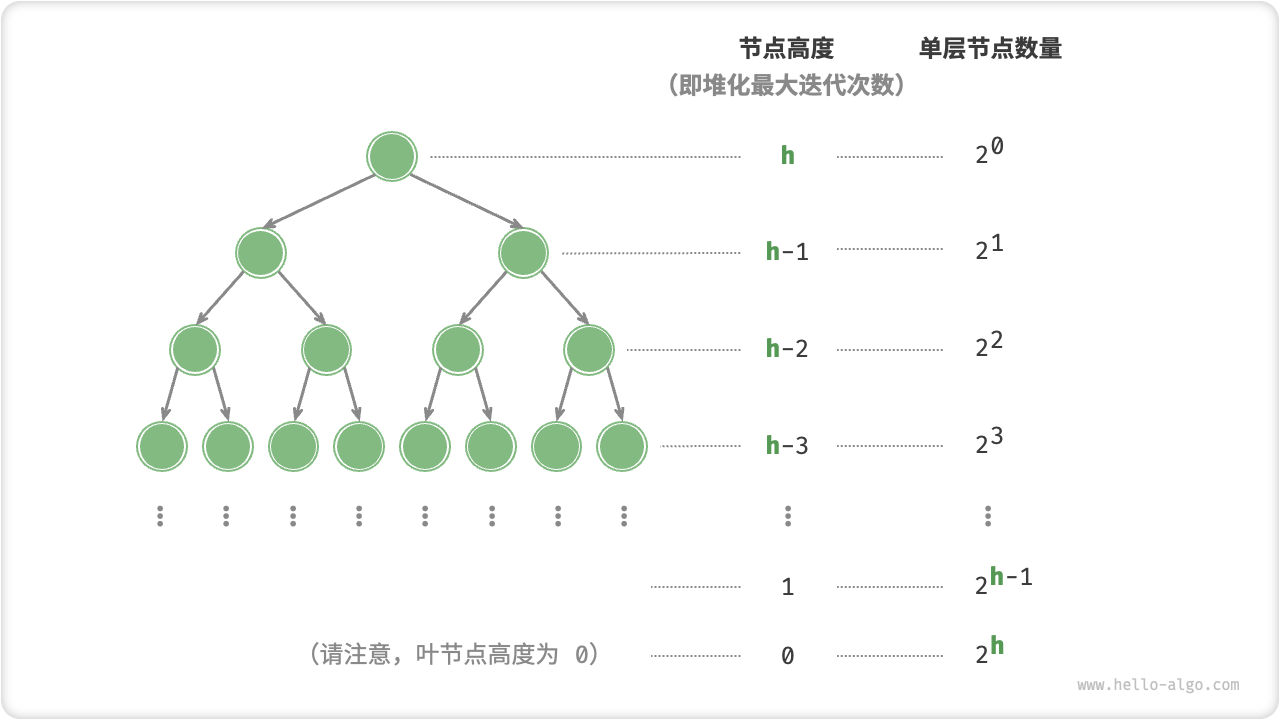
图 8-5 完美二叉树的各层节点数量
如图 8-5 所示,节点“从顶至底堆化”的最大迭代次数等于该节点到叶节点的距离,而该距离正是“节点高度”。因此,我们可以将各层的“节点数量 \(\times\) 节点高度”求和,从而得到所有节点的堆化迭代次数的总和。
\[
T(h) = 2^0h + 2^1(h-1) + 2^2(h-2) + \dots + 2^{(h-1)}\times1
\]
化简上式需要借助中学的数列知识,先对 \(T(h)\) 乘以 \(2\) ,得到:
\[
\begin{aligned}
T(h) & = 2^0h + 2^1(h-1) + 2^2(h-2) + \dots + 2^{h-1}\times1 \newline
2 T(h) & = 2^1h + 2^2(h-1) + 2^3(h-2) + \dots + 2^{h}\times1 \newline
\end{aligned}
\]
使用错位相减法,用下式 \(2 T(h)\) 减去上式 \(T(h)\) ,可得:
\[
2T(h) - T(h) = T(h) = -2^0h + 2^1 + 2^2 + \dots + 2^{h-1} + 2^h
\]
观察上式,发现 \(T(h)\) 是一个等比数列,可直接使用求和公式,得到时间复杂度为:
\[
\begin{aligned}
T(h) & = 2 \frac{1 - 2^h}{1 - 2} - h \newline
& = 2^{h+1} - h - 2 \newline
& = O(2^h)
\end{aligned}
\]
进一步地,高度为 \(h\) 的完美二叉树的节点数量为 \(n = 2^{h+1} - 1\) ,易得复杂度为 \(O(2^h) = O(n)\) 。以上推算表明,输入列表并建堆的时间复杂度为 \(O(n)\) ,非常高效。
