9.3. 图的遍历¶
图与树的关系
树代表的是“一对多”的关系,而图则自由度更高,可以代表任意“多对多”关系。本质上,可以把树看作是图的一类特例。那么显然,树遍历操作也是图遍历操作的一个特例,两者的方法是非常类似的,建议你在学习本章节的过程中将两者融会贯通。
「图」与「树」都是非线性数据结构,都需要使用「搜索算法」来实现遍历操作。
类似地,图的遍历方式也分为两种,即「广度优先遍历 Breadth-First Traversal」和「深度优先遍历 Depth-First Travsersal」,也称「广度优先搜索 Breadth-First Search」和「深度优先搜索 Depth-First Search」,简称为 BFS 和 DFS 。
9.3.1. 广度优先遍历¶
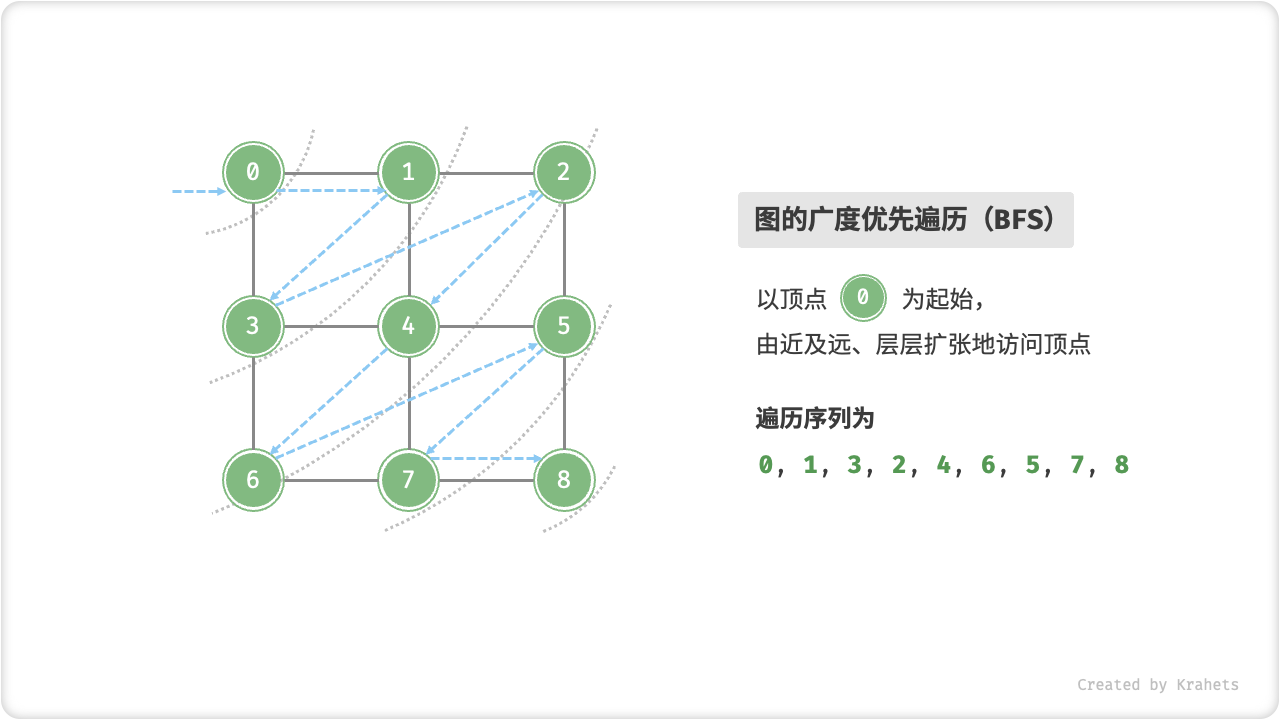
广度优先遍历优是一种由近及远的遍历方式,从距离最近的顶点开始访问,并一层层向外扩张。具体地,从某个顶点出发,先遍历该顶点的所有邻接顶点,随后遍历下个顶点的所有邻接顶点,以此类推……
算法实现¶
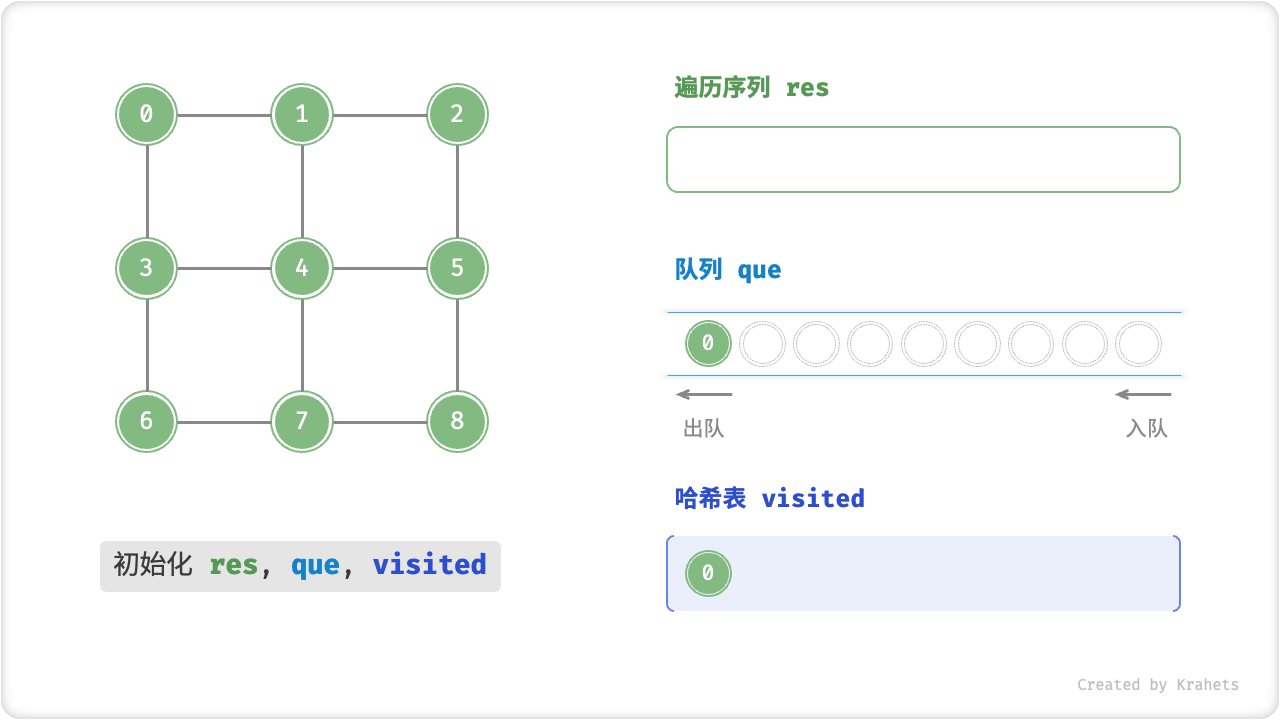
BFS 常借助「队列」来实现。队列具有“先入先出”的性质,这与 BFS “由近及远”的思想是异曲同工的。
- 将遍历起始顶点
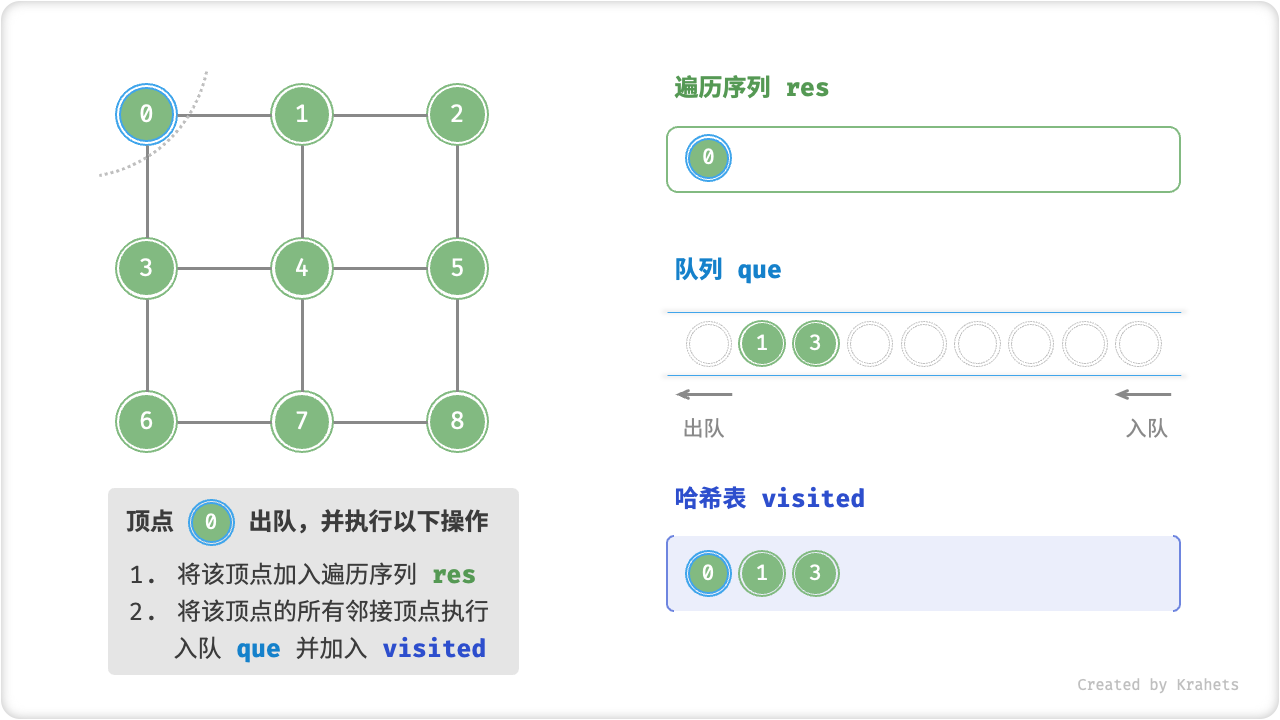
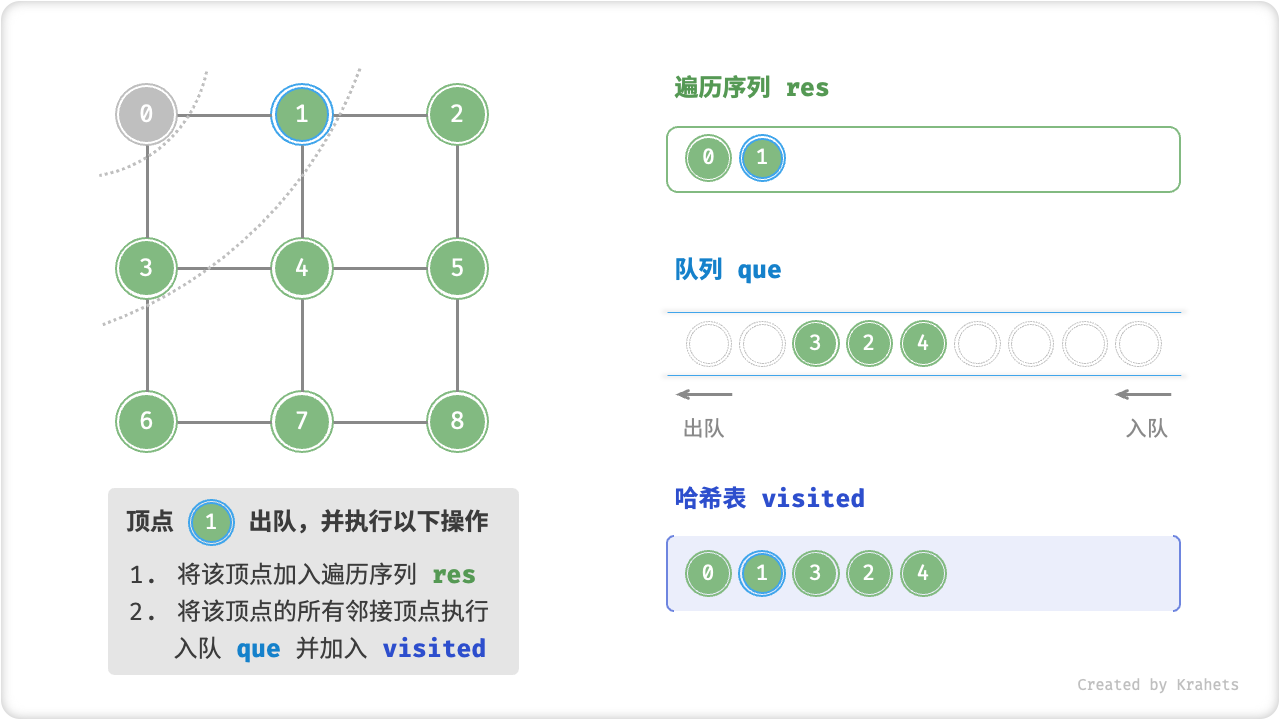
startVet加入队列,并开启循环; - 在循环的每轮迭代中,弹出队首顶点弹出并记录访问,并将该顶点的所有邻接顶点加入到队列尾部;
- 循环
2.,直到所有顶点访问完成后结束;
为了防止重复遍历顶点,我们需要借助一个哈希表 visited 来记录哪些结点已被访问。
/* 广度优先遍历 BFS */
// 使用邻接表来表示图,以便获取指定顶点的所有邻接顶点
List<Vertex> graphBFS(GraphAdjList graph, Vertex startVet) {
// 顶点遍历序列
List<Vertex> res = new ArrayList<>();
// 哈希表,用于记录已被访问过的顶点
Set<Vertex> visited = new HashSet<>() {{ add(startVet); }};
// 队列用于实现 BFS
Queue<Vertex> que = new LinkedList<>() {{ offer(startVet); }};
// 以顶点 vet 为起点,循环直至访问完所有顶点
while (!que.isEmpty()) {
Vertex vet = que.poll(); // 队首顶点出队
res.add(vet); // 记录访问顶点
// 遍历该顶点的所有邻接顶点
for (Vertex adjVet : graph.adjList.get(vet)) {
if (visited.contains(adjVet))
continue; // 跳过已被访问过的顶点
que.offer(adjVet); // 只入队未访问的顶点
visited.add(adjVet); // 标记该顶点已被访问
}
}
// 返回顶点遍历序列
return res;
}
""" 广度优先遍历 BFS """
# 使用邻接表来表示图,以便获取指定顶点的所有邻接顶点
def graph_bfs(graph: GraphAdjList, start_vet: Vertex) -> List[Vertex]:
# 顶点遍历序列
res = []
# 哈希表,用于记录已被访问过的顶点
visited = set([start_vet])
# 队列用于实现 BFS
que = collections.deque([start_vet])
# 以顶点 vet 为起点,循环直至访问完所有顶点
while len(que) > 0:
vet = que.popleft() # 队首顶点出队
res.append(vet) # 记录访问顶点
# 遍历该顶点的所有邻接顶点
for adj_vet in graph.adj_list[vet]:
if adj_vet in visited:
continue # 跳过已被访问过的顶点
que.append(adj_vet) # 只入队未访问的顶点
visited.add(adj_vet) # 标记该顶点已被访问
# 返回顶点遍历序列
return res
/* 广度优先遍历 BFS */
// 使用邻接表来表示图,以便获取指定顶点的所有邻接顶点
func graphBFS(graph: GraphAdjList, startVet: Vertex) -> [Vertex] {
// 顶点遍历序列
var res: [Vertex] = []
// 哈希表,用于记录已被访问过的顶点
var visited: Set<Vertex> = [startVet]
// 队列用于实现 BFS
var que: [Vertex] = [startVet]
// 以顶点 vet 为起点,循环直至访问完所有顶点
while !que.isEmpty {
let vet = que.removeFirst() // 队首顶点出队
res.append(vet) // 记录访问顶点
// 遍历该顶点的所有邻接顶点
for adjVet in graph.adjList[vet] ?? [] {
if visited.contains(adjVet) {
continue // 跳过已被访问过的顶点
}
que.append(adjVet) // 只入队未访问的顶点
visited.insert(adjVet) // 标记该顶点已被访问
}
}
// 返回顶点遍历序列
return res
}
代码相对抽象,建议对照以下动画图示来加深理解。
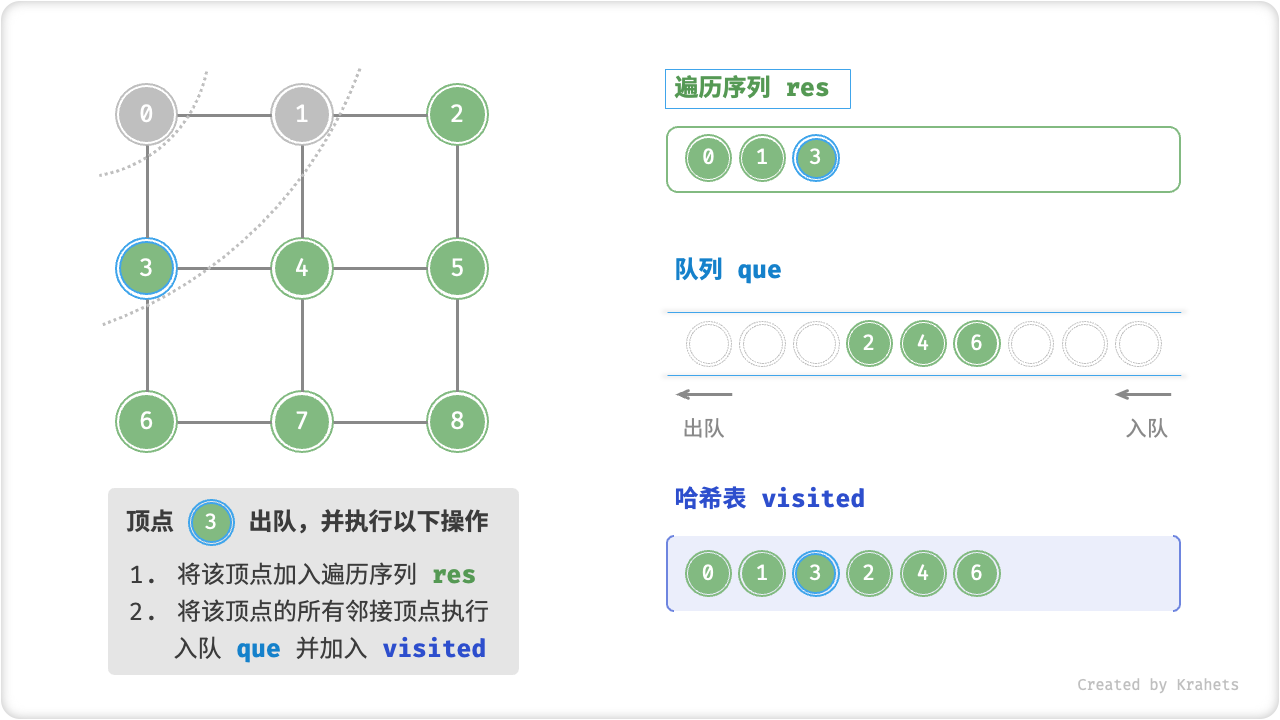
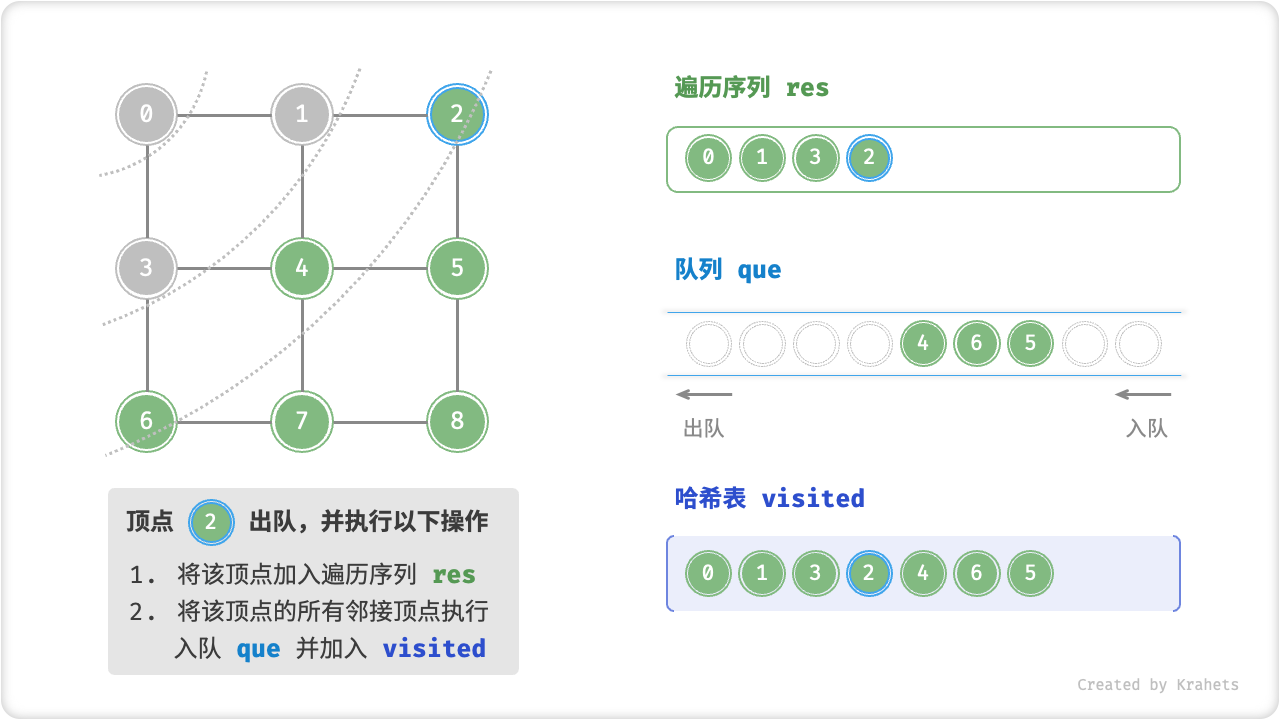
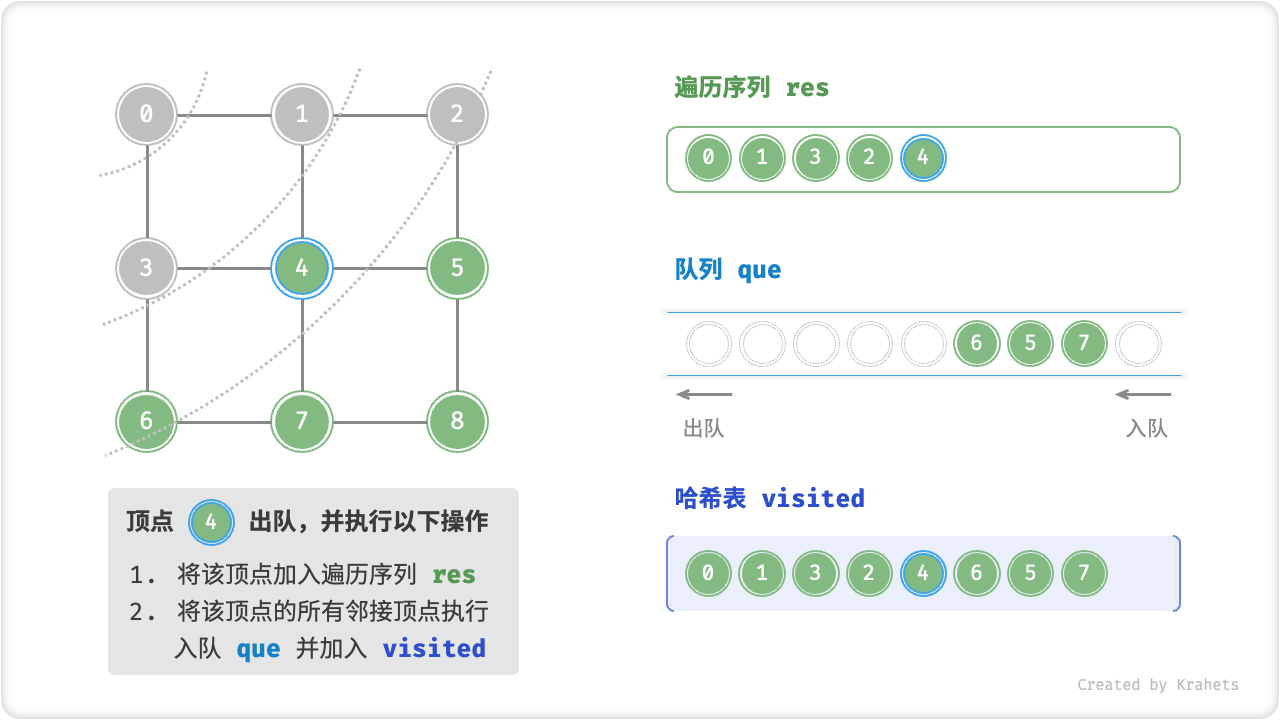
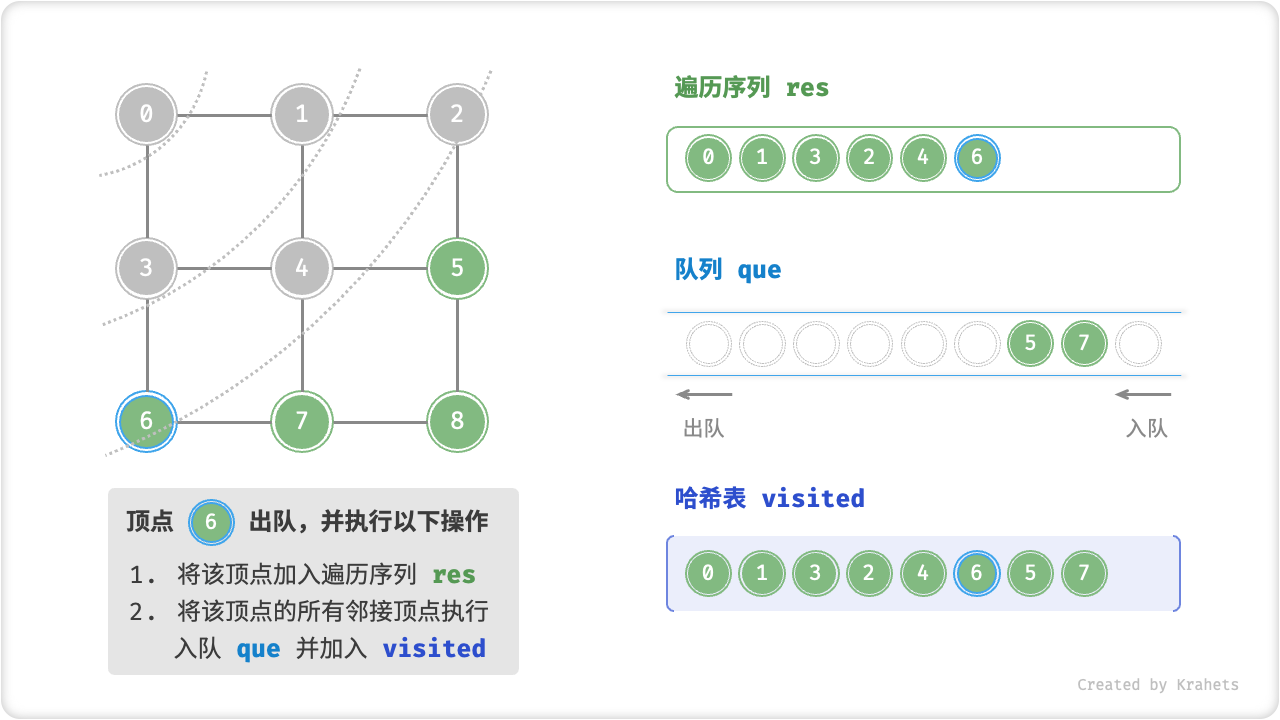
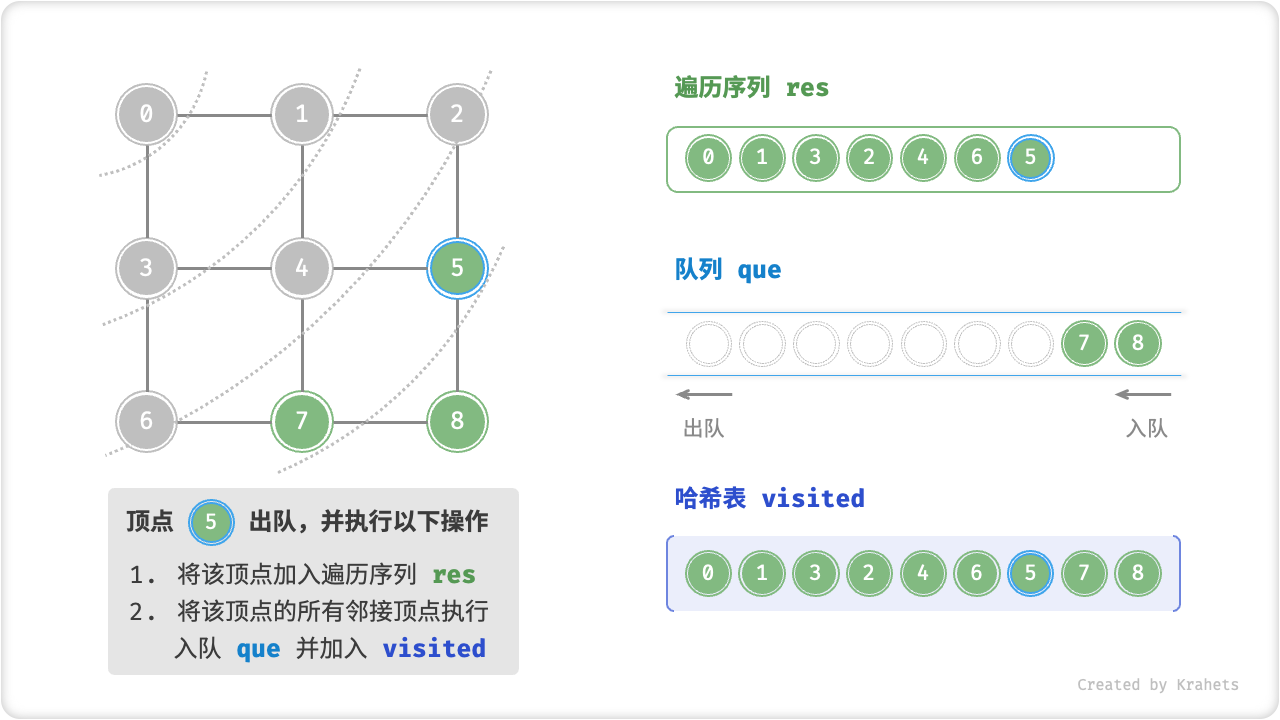
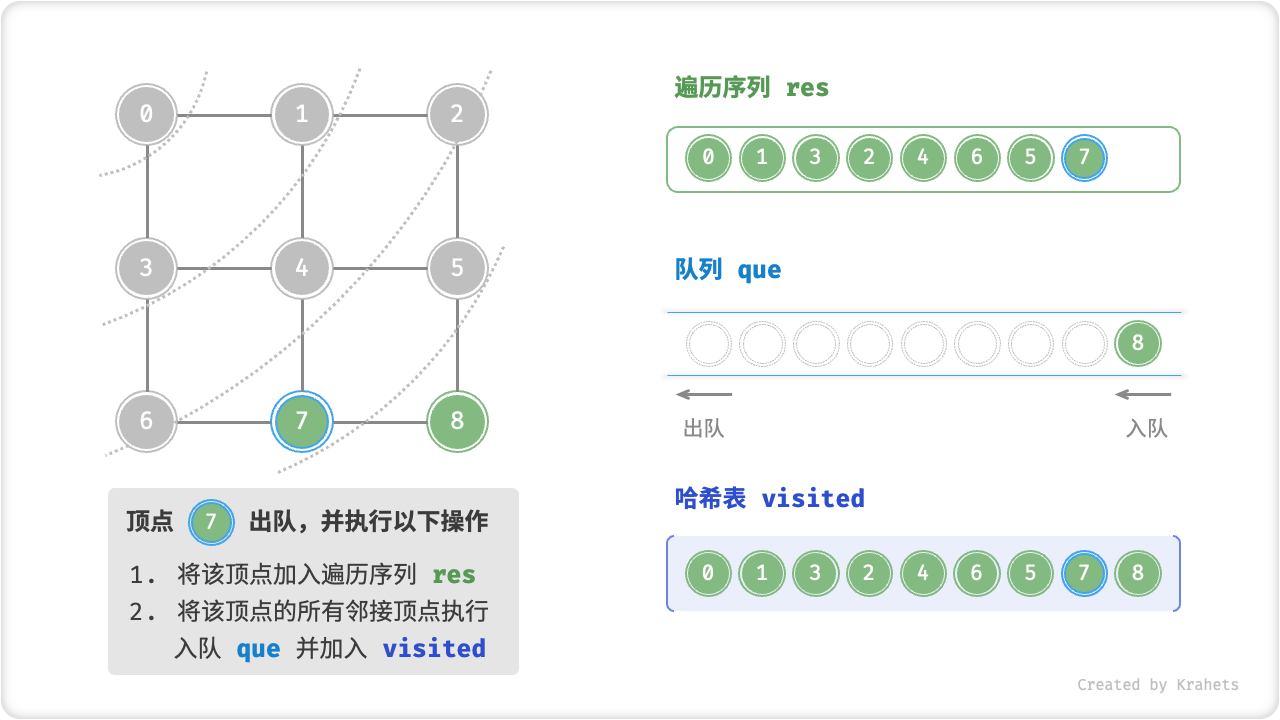
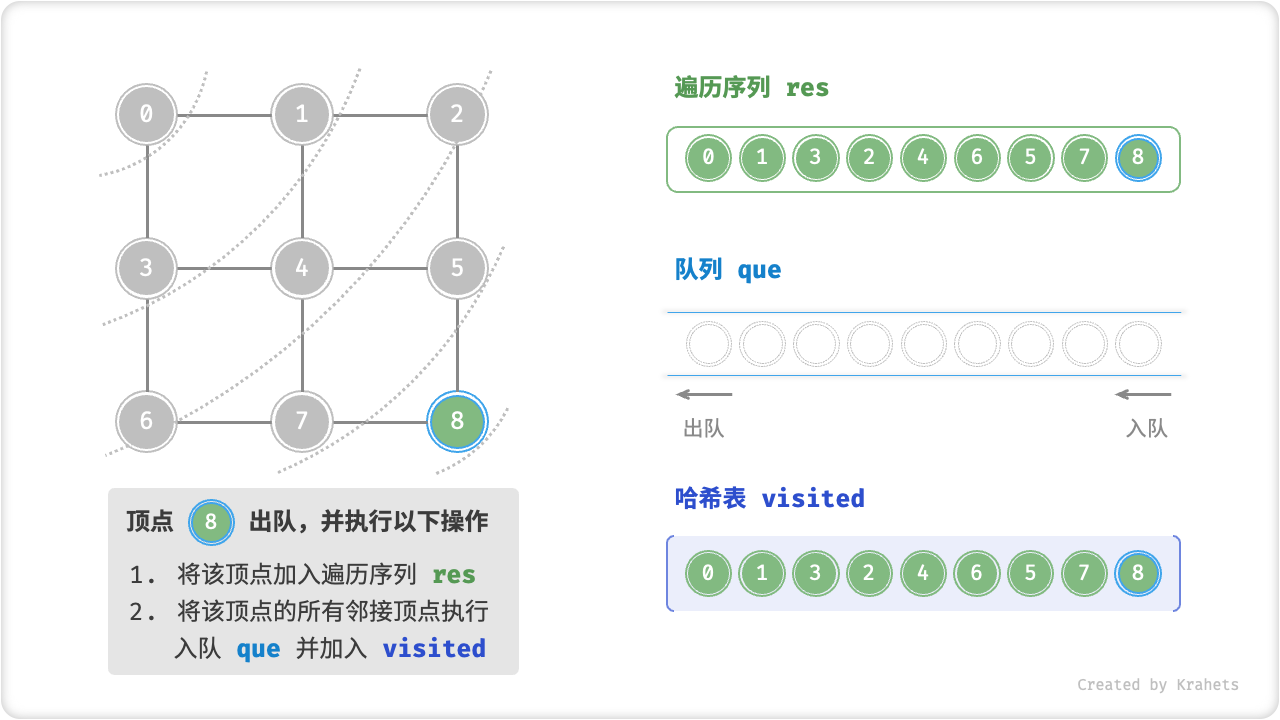
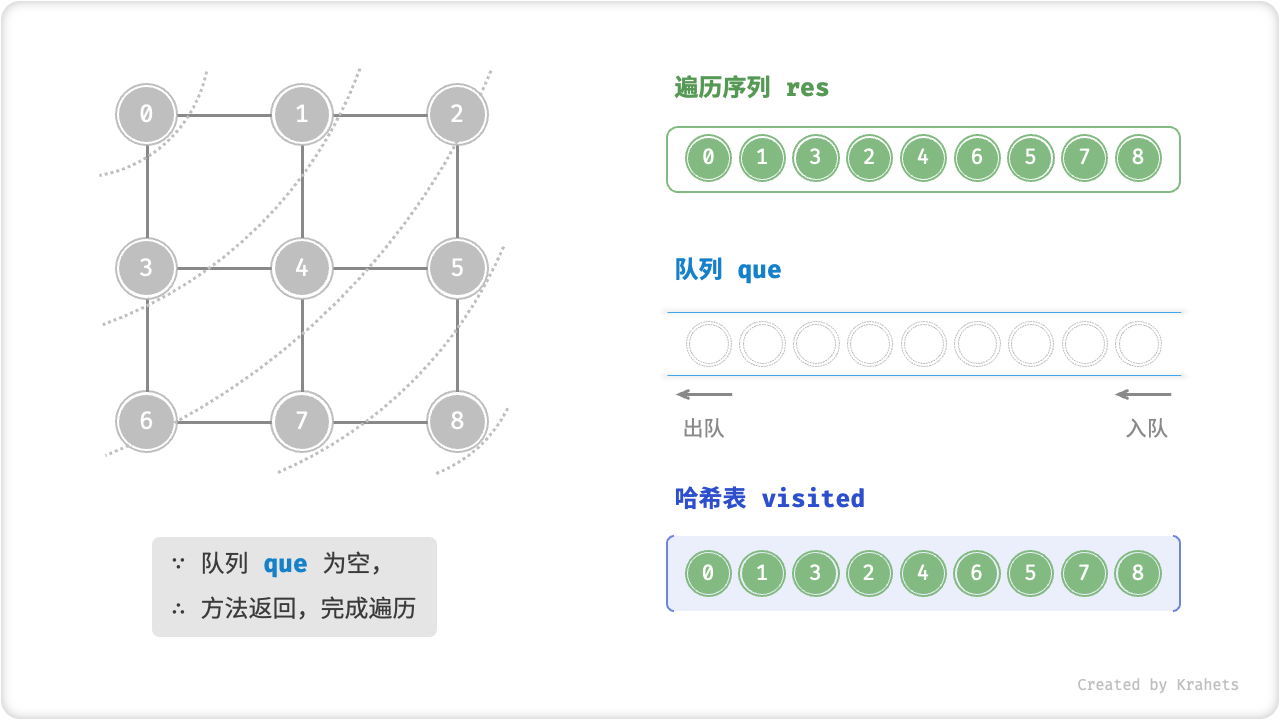
广度优先遍历的序列是否唯一?
不唯一。广度优先遍历只要求“由近及远”,而多个相同距离的顶点的遍历顺序允许被任意打乱。以上图为例,顶点 \(1\) , \(3\) 的访问顺序可以交换、顶点 \(2\) , \(4\) , \(6\) 的访问顺序也可以任意交换、以此类推……
复杂度分析¶
时间复杂度: 所有顶点都会入队、出队一次,使用 \(O(|V|)\) 时间;在遍历邻接顶点的过程中,由于是无向图,因此所有边都会被访问 \(2\) 次,使用 \(O(2|E|)\) 时间;总体使用 \(O(|V| + |E|)\) 时间。
空间复杂度: 列表 res ,哈希表 visited ,队列 que 中的顶点数量最多为 \(|V|\) ,使用 \(O(|V|)\) 空间。
9.3.2. 深度优先遍历¶
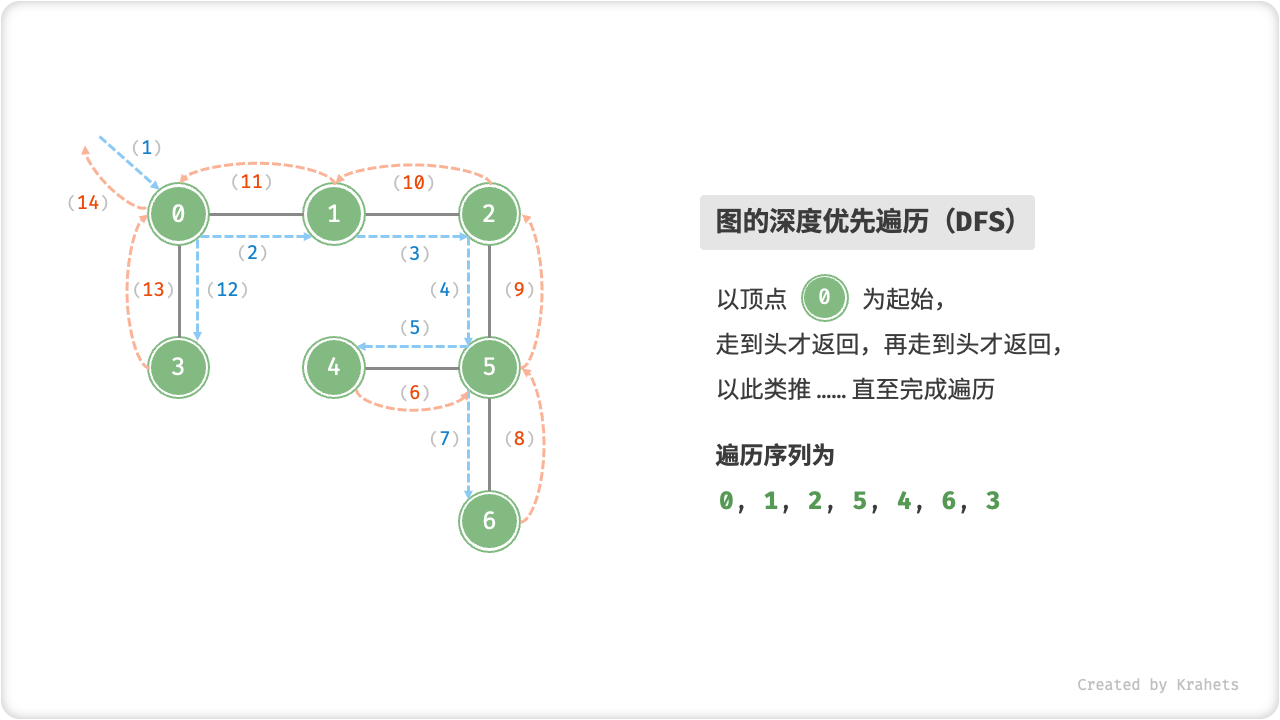
深度优先遍历是一种优先走到底、无路可走再回头的遍历方式。具体地,从某个顶点出发,不断地访问当前结点的某个邻接顶点,直到走到尽头时回溯,再继续走到底 + 回溯,以此类推……直至所有顶点遍历完成时结束。
算法实现¶
这种“走到头 + 回溯”的算法形式一般基于递归来实现。与 BFS 类似,在 DFS 中我们也需要借助一个哈希表 visited 来记录已被访问的顶点,以避免重复访问顶点。
/* 深度优先遍历 DFS 辅助函数 */
void dfs(GraphAdjList graph, Set<Vertex> visited, List<Vertex> res, Vertex vet) {
res.add(vet); // 记录访问顶点
visited.add(vet); // 标记该顶点已被访问
// 遍历该顶点的所有邻接顶点
for (Vertex adjVet : graph.adjList.get(vet)) {
if (visited.contains(adjVet))
continue; // 跳过已被访问过的顶点
// 递归访问邻接顶点
dfs(graph, visited, res, adjVet);
}
}
/* 深度优先遍历 DFS */
// 使用邻接表来表示图,以便获取指定顶点的所有邻接顶点
List<Vertex> graphDFS(GraphAdjList graph, Vertex startVet) {
// 顶点遍历序列
List<Vertex> res = new ArrayList<>();
// 哈希表,用于记录已被访问过的顶点
Set<Vertex> visited = new HashSet<>();
dfs(graph, visited, res, startVet);
return res;
}
""" 深度优先遍历 DFS 辅助函数 """
def dfs(graph: GraphAdjList, visited: Set[Vertex], res: List[Vertex], vet: Vertex):
res.append(vet) # 记录访问顶点
visited.add(vet) # 标记该顶点已被访问
# 遍历该顶点的所有邻接顶点
for adjVet in graph.adj_list[vet]:
if adjVet in visited:
continue # 跳过已被访问过的顶点
# 递归访问邻接顶点
dfs(graph, visited, res, adjVet)
""" 深度优先遍历 DFS """
# 使用邻接表来表示图,以便获取指定顶点的所有邻接顶点
def graph_dfs(graph: GraphAdjList, start_vet: Vertex) -> List[Vertex]:
# 顶点遍历序列
res = []
# 哈希表,用于记录已被访问过的顶点
visited = set()
dfs(graph, visited, res, start_vet)
return res
/* 深度优先遍历 DFS 辅助函数 */
func dfs(graph: GraphAdjList, visited: inout Set<Vertex>, res: inout [Vertex], vet: Vertex) {
res.append(vet) // 记录访问顶点
visited.insert(vet) // 标记该顶点已被访问
// 遍历该顶点的所有邻接顶点
for adjVet in graph.adjList[vet] ?? [] {
if visited.contains(adjVet) {
continue // 跳过已被访问过的顶点
}
// 递归访问邻接顶点
dfs(graph: graph, visited: &visited, res: &res, vet: adjVet)
}
}
/* 深度优先遍历 DFS */
// 使用邻接表来表示图,以便获取指定顶点的所有邻接顶点
func graphDFS(graph: GraphAdjList, startVet: Vertex) -> [Vertex] {
// 顶点遍历序列
var res: [Vertex] = []
// 哈希表,用于记录已被访问过的顶点
var visited: Set<Vertex> = []
dfs(graph: graph, visited: &visited, res: &res, vet: startVet)
return res
}
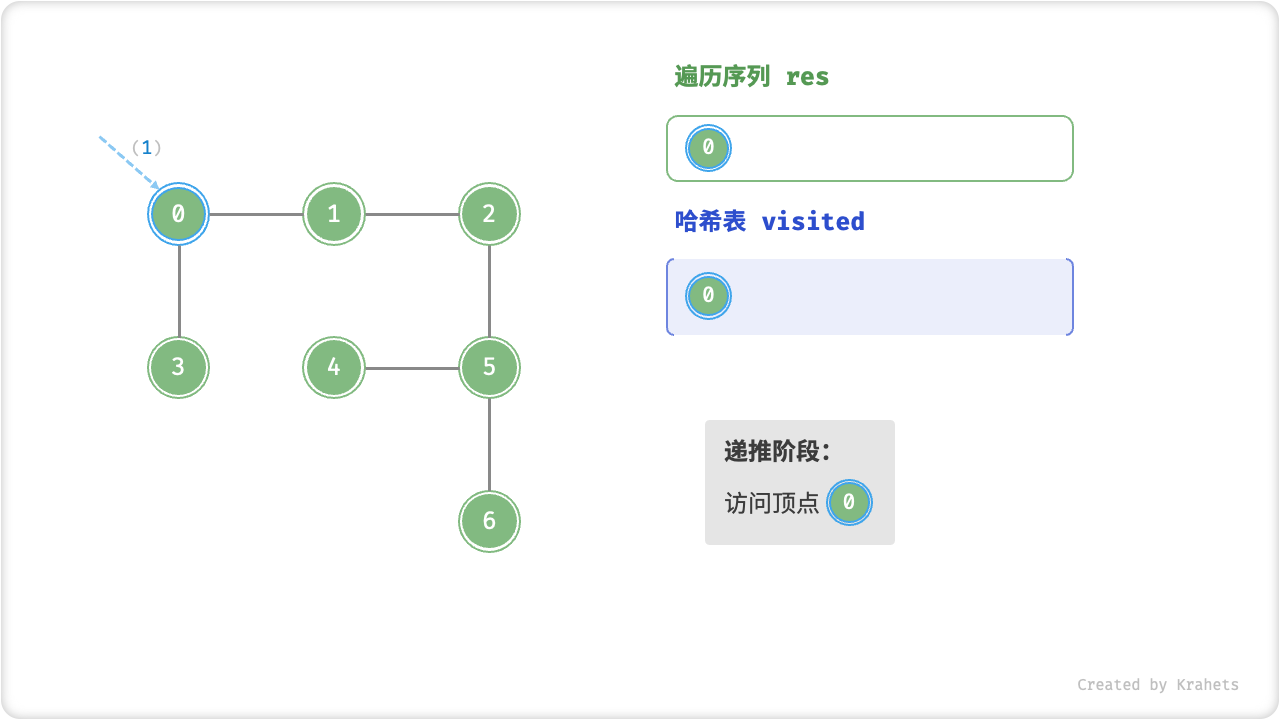
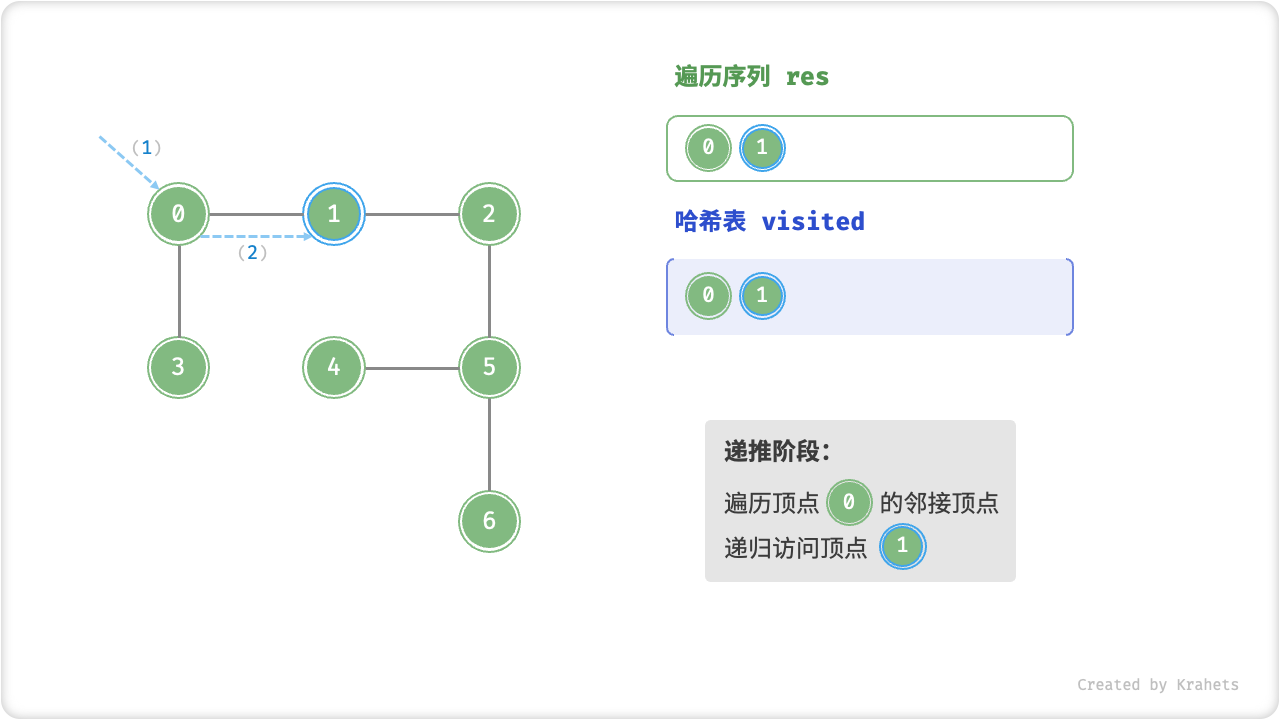
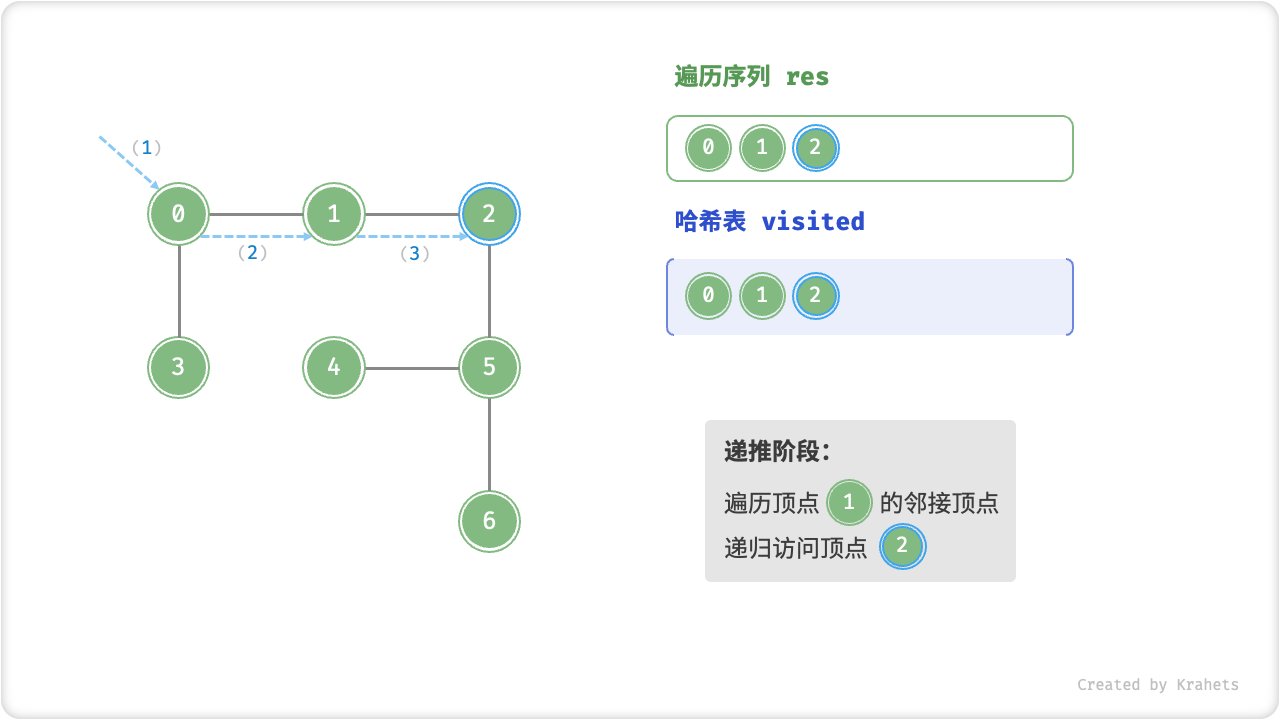
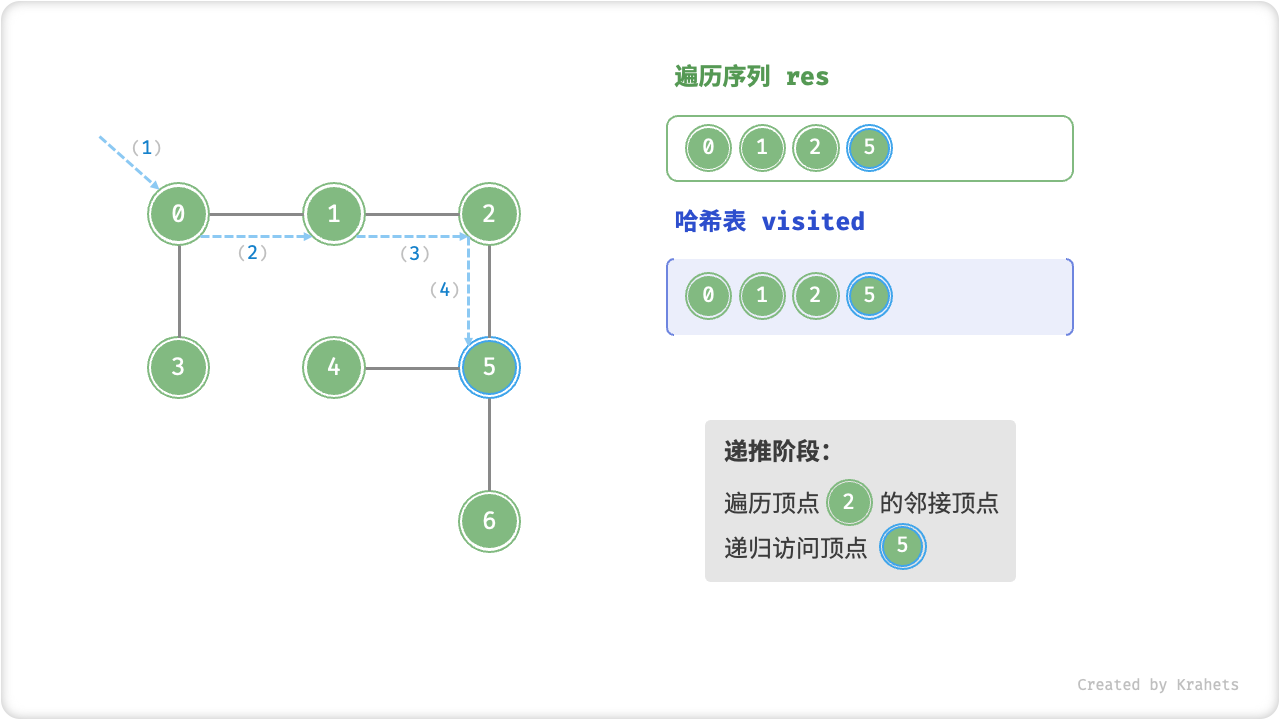
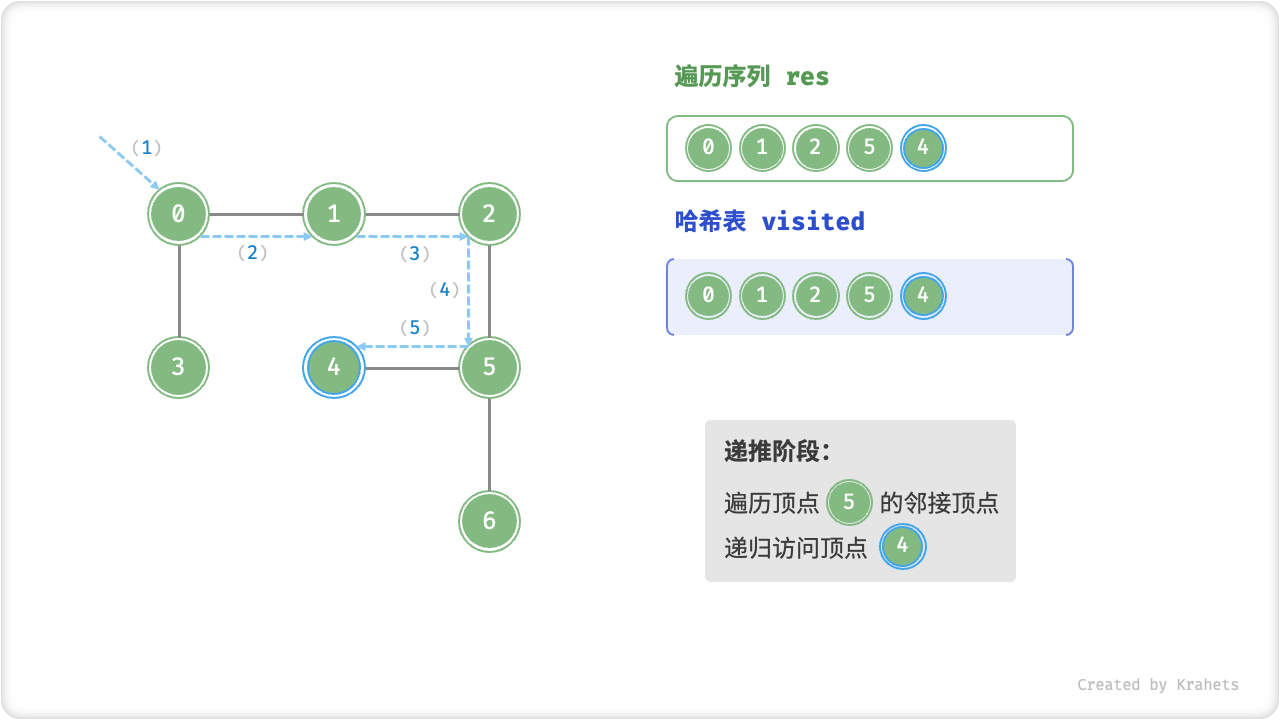
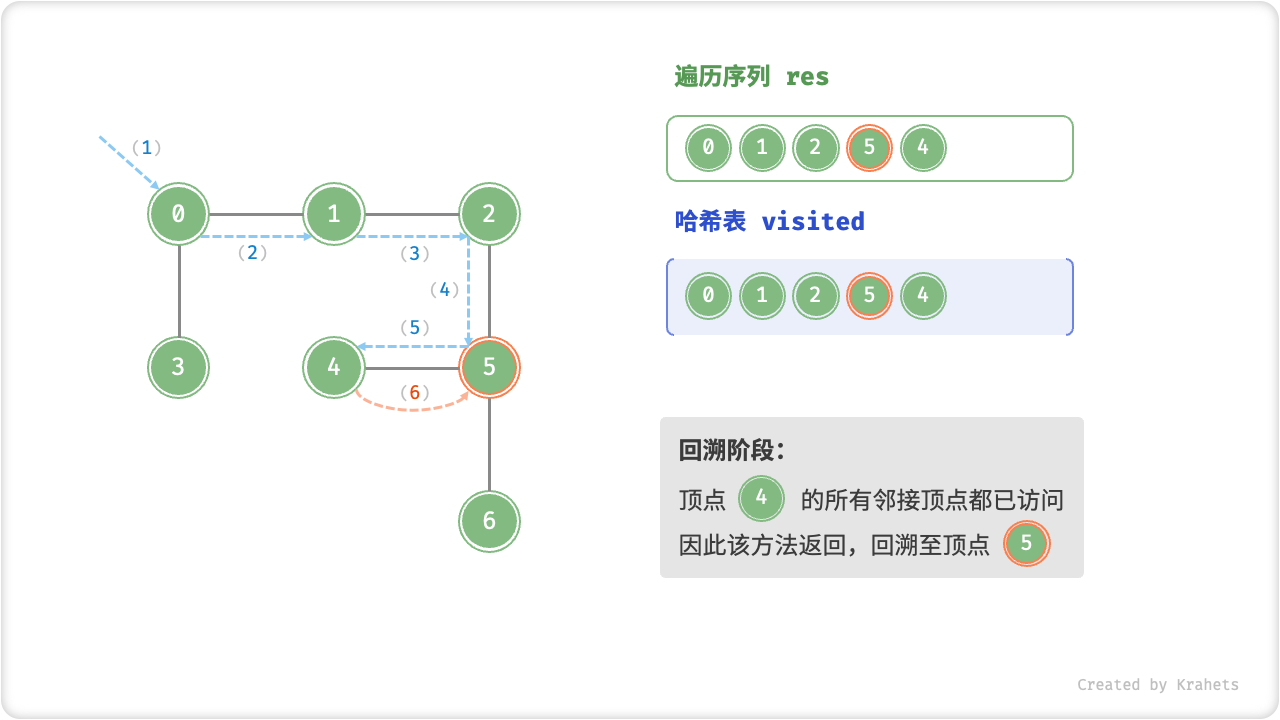
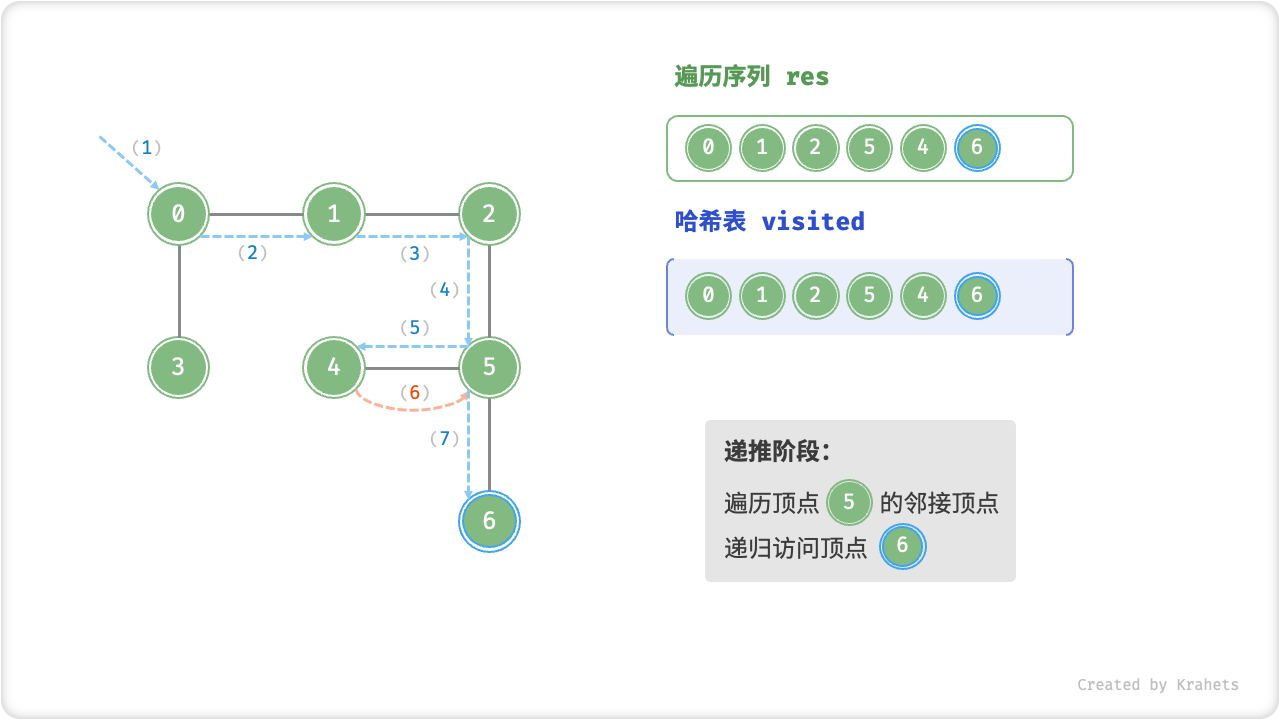
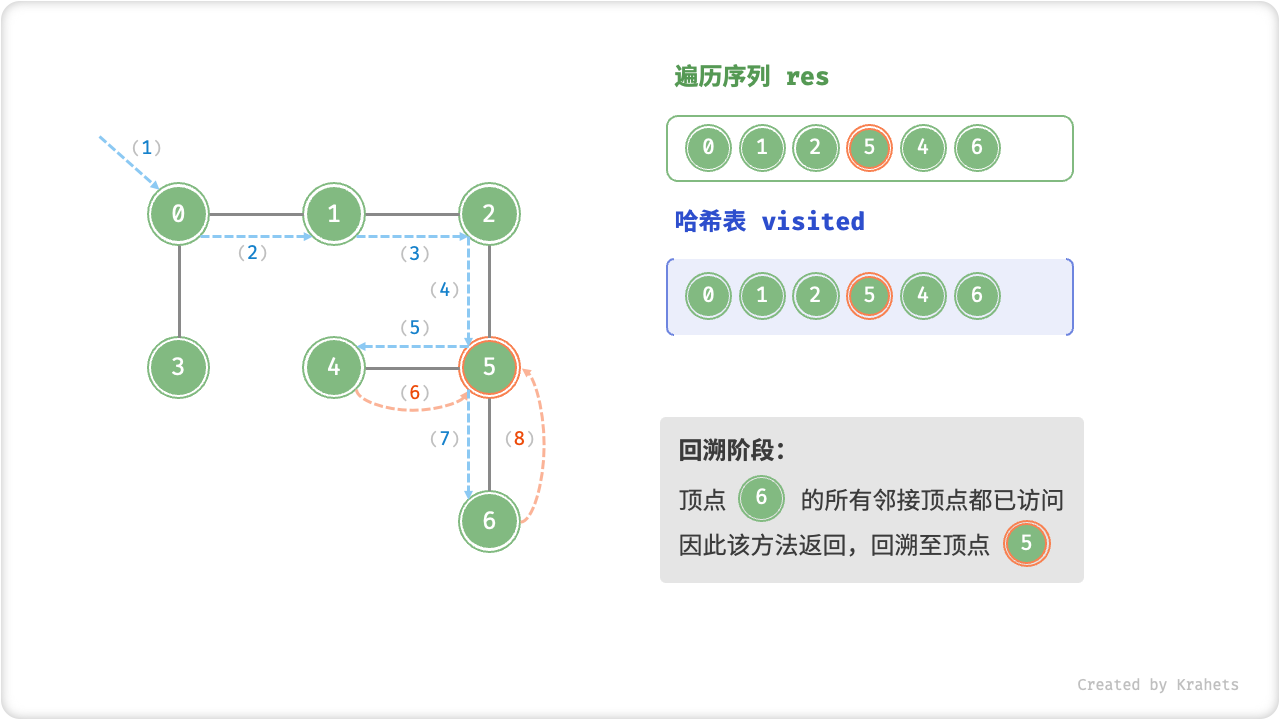
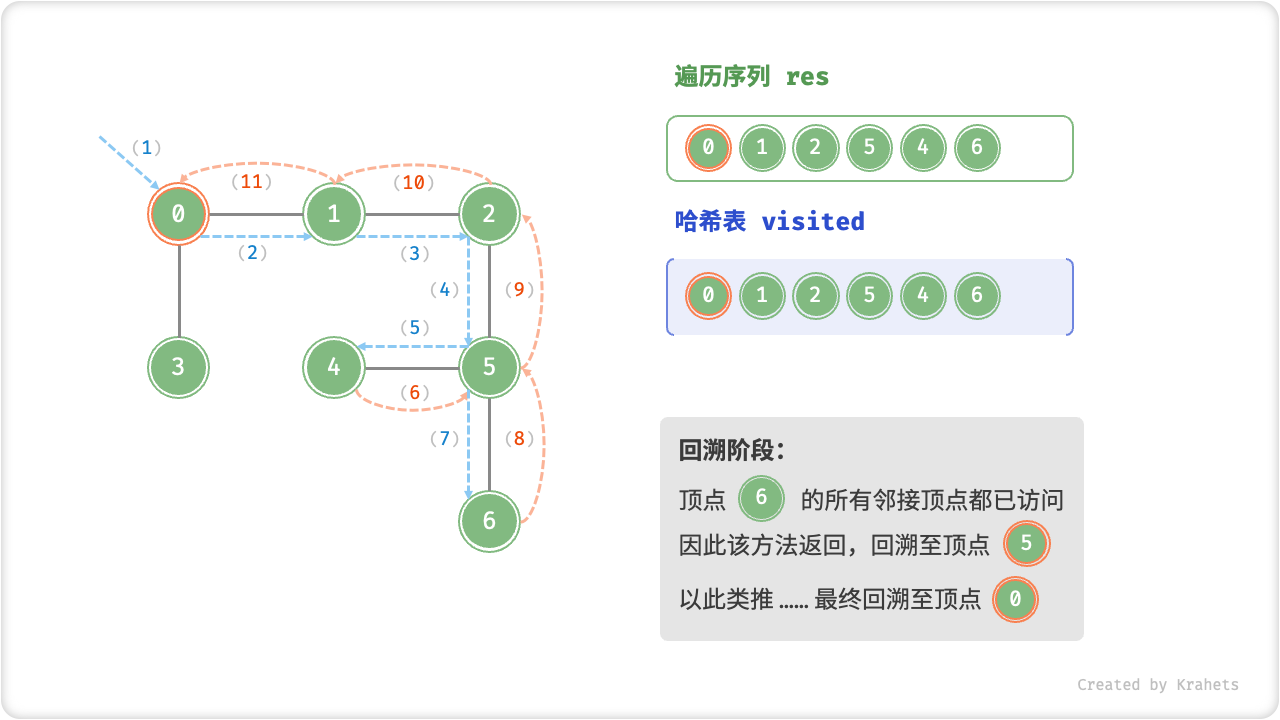
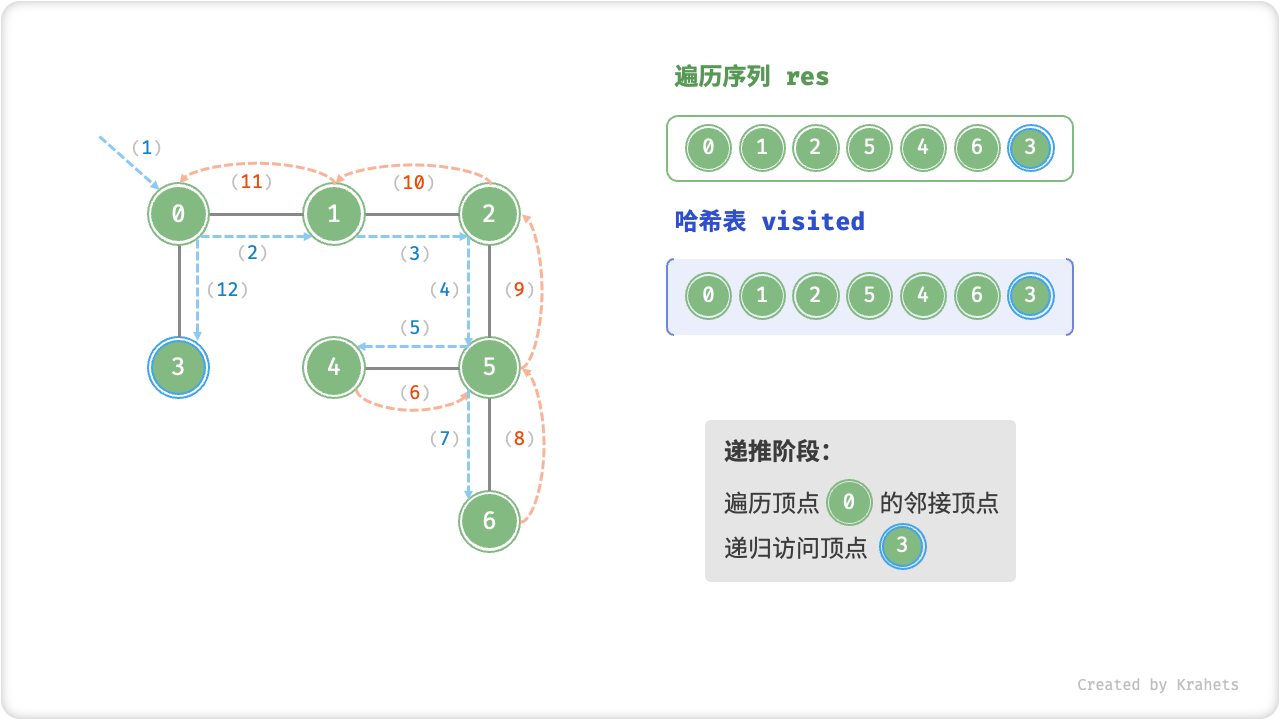
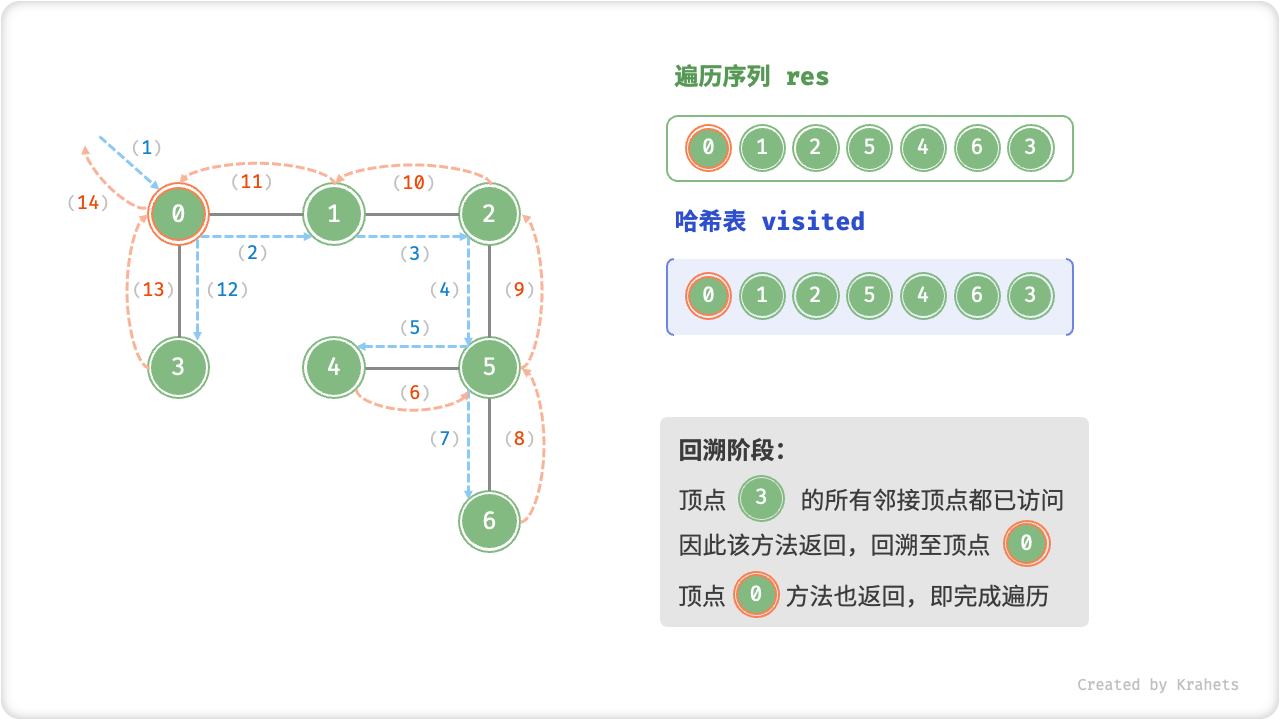
深度优先遍历的算法流程如下图所示,其中
- 直虚线代表向下递推,代表开启了一个新的递归方法来访问新顶点;
- 曲虚线代表向上回溯,代表此递归方法已经返回,回溯到了开启此递归方法的位置;
为了加深理解,请你将图示与代码结合起来,在脑中(或者用笔画下来)模拟整个 DFS 过程,包括每个递归方法何时开启、何时返回。
深度优先遍历的序列是否唯一?
与广度优先遍历类似,深度优先遍历序列的顺序也不是唯一的。给定某顶点,先往哪个方向探索都行,都是深度优先遍历。
以树的遍历为例,“根 \(\rightarrow\) 左 \(\rightarrow\) 右”、“左 \(\rightarrow\) 根 \(\rightarrow\) 右”、“左 \(\rightarrow\) 右 \(\rightarrow\) 根”分别对应前序、中序、后序遍历,体现三种不同的遍历优先级,而三者都属于深度优先遍历。
复杂度分析¶
时间复杂度: 所有顶点都被访问一次;所有边都被访问了 \(2\) 次,使用 \(O(2|E|)\) 时间;总体使用 \(O(|V| + |E|)\) 时间。
空间复杂度: 列表 res ,哈希表 visited 顶点数量最多为 \(|V|\) ,递归深度最大为 \(|V|\) ,因此使用 \(O(|V|)\) 空间。