5.1.   栈

「栈 Stack」是一种遵循先入后出（First In, Last Out）原则的线性数据结构。

我们可以将栈类比为桌面上的一摞盘子，如果需要拿出底部的盘子，则需要先将上面的盘子依次取出。我们将盘子替换为各种类型的元素（如整数、字符、对象等），就得到了栈数据结构。

在栈中，我们把堆叠元素的顶部称为「栈顶」，底部称为「栈底」。将把元素添加到栈顶的操作叫做「入栈」，而删除栈顶元素的操作叫做「出栈」。

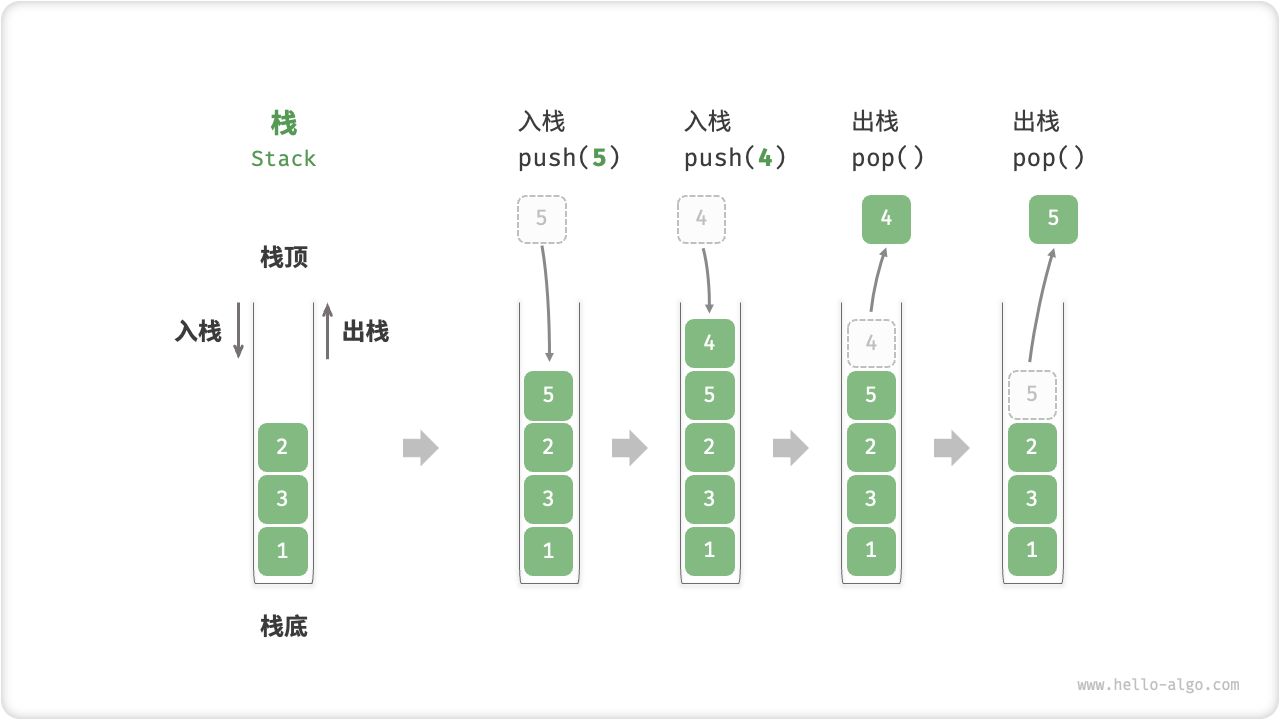
Fig. 栈的先入后出规则

5.1.1.   栈常用操作

栈的常用操作如下表所示，具体的方法名需要根据所使用的编程语言来确定。在此，我们以常见的 push() , pop() , peek() 命名为例。

方法	描述	时间复杂度
push()	元素入栈（添加至栈顶）	\(O(1)\)
pop()	栈顶元素出栈	\(O(1)\)
peek()	访问栈顶元素	\(O(1)\)

通常情况下，我们可以直接使用编程语言内置的栈类。然而，某些语言可能没有专门提供栈类，这时我们可以将该语言的「数组」或「链表」视作栈来使用，并通过“脑补”来忽略与栈无关的操作。

JavaC++PythonGoJavaScriptTypeScriptCC#SwiftZig

stack.java

/* 初始化栈 */
Stack<Integer> stack = new Stack<>();

/* 元素入栈 */
stack.push(1);
stack.push(3);
stack.push(2);
stack.push(5);
stack.push(4);

/* 访问栈顶元素 */
int peek = stack.peek();

/* 元素出栈 */
int pop = stack.pop();

/* 获取栈的长度 */
int size = stack.size();

/* 判断是否为空 */
boolean isEmpty = stack.isEmpty();

stack.cpp

/* 初始化栈 */
stack<int> stack;

/* 元素入栈 */
stack.push(1);
stack.push(3);
stack.push(2);
stack.push(5);
stack.push(4);

/* 访问栈顶元素 */
int top = stack.top();

/* 元素出栈 */
stack.pop(); // 无返回值

/* 获取栈的长度 */
int size = stack.size();

/* 判断是否为空 */
bool empty = stack.empty();

stack.py

# 初始化栈
# Python 没有内置的栈类，可以把 List 当作栈来使用 
stack: List[int] = []

# 元素入栈
stack.append(1)
stack.append(3)
stack.append(2)
stack.append(5)
stack.append(4)

# 访问栈顶元素
peek: int = stack[-1]

# 元素出栈
pop: int = stack.pop()

# 获取栈的长度
size: int = len(stack)

# 判断是否为空
is_empty: bool = len(stack) == 0

stack_test.go

/* 初始化栈 */
// 在 Go 中，推荐将 Slice 当作栈来使用
var stack []int

/* 元素入栈 */
stack = append(stack, 1)
stack = append(stack, 3)
stack = append(stack, 2)
stack = append(stack, 5)
stack = append(stack, 4)

/* 访问栈顶元素 */
peek := stack[len(stack)-1]

/* 元素出栈 */
pop := stack[len(stack)-1]
stack = stack[:len(stack)-1]

/* 获取栈的长度 */
size := len(stack)

/* 判断是否为空 */
isEmpty := len(stack) == 0

stack.js

/* 初始化栈 */
// Javascript 没有内置的栈类，可以把 Array 当作栈来使用 
const stack = [];

/* 元素入栈 */
stack.push(1);
stack.push(3);
stack.push(2);
stack.push(5);
stack.push(4);

/* 访问栈顶元素 */
const peek = stack[stack.length-1];

/* 元素出栈 */
const pop = stack.pop();

/* 获取栈的长度 */
const size = stack.length;

/* 判断是否为空 */
const is_empty = stack.length === 0;

stack.ts

/* 初始化栈 */
// Typescript 没有内置的栈类，可以把 Array 当作栈来使用 
const stack: number[] = [];

/* 元素入栈 */
stack.push(1);
stack.push(3);
stack.push(2);
stack.push(5);
stack.push(4);

/* 访问栈顶元素 */
const peek = stack[stack.length - 1];

/* 元素出栈 */
const pop = stack.pop();

/* 获取栈的长度 */
const size = stack.length;

/* 判断是否为空 */
const is_empty = stack.length === 0;

stack.c

stack.cs

/* 初始化栈 */
Stack<int> stack = new ();

/* 元素入栈 */
stack.Push(1);
stack.Push(3);
stack.Push(2);
stack.Push(5);
stack.Push(4);

/* 访问栈顶元素 */
int peek = stack.Peek();

/* 元素出栈 */
int pop = stack.Pop();

/* 获取栈的长度 */
int size = stack.Count();

/* 判断是否为空 */
bool isEmpty = stack.Count()==0;

stack.swift

/* 初始化栈 */
// Swift 没有内置的栈类，可以把 Array 当作栈来使用
var stack: [Int] = []

/* 元素入栈 */
stack.append(1)
stack.append(3)
stack.append(2)
stack.append(5)
stack.append(4)

/* 访问栈顶元素 */
let peek = stack.last!

/* 元素出栈 */
let pop = stack.removeLast()

/* 获取栈的长度 */
let size = stack.count

/* 判断是否为空 */
let isEmpty = stack.isEmpty

stack.zig

5.1.2.   栈的实现

为了深入了解栈的运行机制，我们来尝试自己实现一个栈类。

栈遵循先入后出的原则，因此我们只能在栈顶添加或删除元素。然而，数组和链表都可以在任意位置添加和删除元素，因此栈可以被视为一种受限制的数组或链表。换句话说，我们可以“屏蔽”数组或链表的部分无关操作，使其对外表现的逻辑符合栈的特性。

基于链表的实现

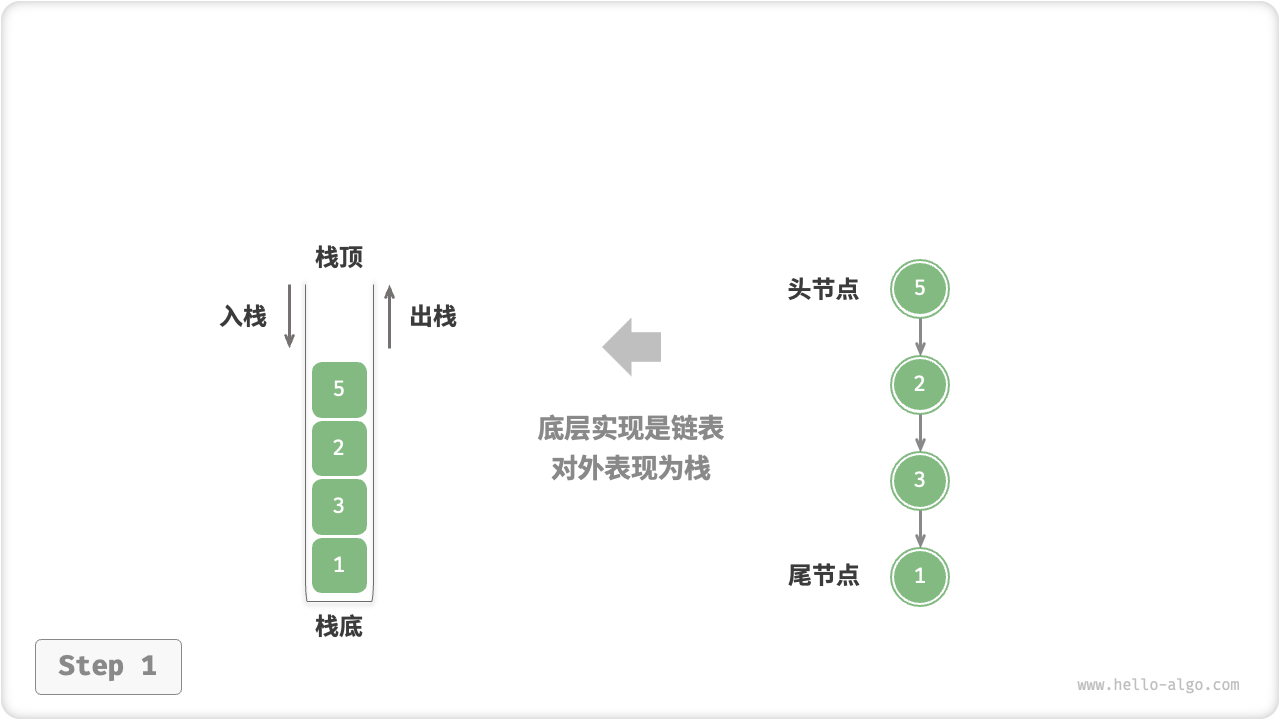
使用链表来实现栈时，我们可以将链表的头节点视为栈顶，尾节点视为栈底。

对于入栈操作，我们只需将元素插入链表头部，这种节点插入方法被称为“头插法”。而对于出栈操作，只需将头节点从链表中删除即可。

LinkedListStackpush()pop()

以下是基于链表实现栈的示例代码。

JavaC++PythonGoJavaScriptTypeScriptCC#SwiftZig

linkedlist_stack.java

/* 基于链表实现的栈 */
class LinkedListStack {
    private ListNode stackPeek; // 将头节点作为栈顶
    private int stkSize = 0; // 栈的长度

    public LinkedListStack() {
        stackPeek = null;
    }

    /* 获取栈的长度 */
    public int size() {
        return stkSize;
    }

    /* 判断栈是否为空 */
    public boolean isEmpty() {
        return size() == 0;
    }

    /* 入栈 */
    public void push(int num) {
        ListNode node = new ListNode(num);
        node.next = stackPeek;
        stackPeek = node;
        stkSize++;
    }

    /* 出栈 */
    public int pop() {
        int num = peek();
        stackPeek = stackPeek.next;
        stkSize--;
        return num;
    }

    /* 访问栈顶元素 */
    public int peek() {
        if (size() == 0)
            throw new EmptyStackException();
        return stackPeek.val;
    }

    /* 将 List 转化为 Array 并返回 */
    public int[] toArray() {
        ListNode node = stackPeek;
        int[] res = new int[size()];
        for (int i = res.length - 1; i >= 0; i--) {
            res[i] = node.val;
            node = node.next;
        }
        return res;
    }
}

linkedlist_stack.cpp

/* 基于链表实现的栈 */
class LinkedListStack {
  private:
    ListNode *stackTop; // 将头节点作为栈顶
    int stkSize;        // 栈的长度

  public:
    LinkedListStack() {
        stackTop = nullptr;
        stkSize = 0;
    }

    ~LinkedListStack() {
        // 遍历链表删除节点，释放内存
        freeMemoryLinkedList(stackTop);
    }

    /* 获取栈的长度 */
    int size() {
        return stkSize;
    }

    /* 判断栈是否为空 */
    bool empty() {
        return size() == 0;
    }

    /* 入栈 */
    void push(int num) {
        ListNode *node = new ListNode(num);
        node->next = stackTop;
        stackTop = node;
        stkSize++;
    }

    /* 出栈 */
    void pop() {
        int num = top();
        ListNode *tmp = stackTop;
        stackTop = stackTop->next;
        // 释放内存
        delete tmp;
        stkSize--;
    }

    /* 访问栈顶元素 */
    int top() {
        if (size() == 0)
            throw out_of_range("栈为空");
        return stackTop->val;
    }

    /* 将 List 转化为 Array 并返回 */
    vector<int> toVector() {
        ListNode *node = stackTop;
        vector<int> res(size());
        for (int i = res.size() - 1; i >= 0; i--) {
            res[i] = node->val;
            node = node->next;
        }
        return res;
    }
};

linkedlist_stack.py

class LinkedListStack:
    """基于链表实现的栈"""

    def __init__(self):
        """构造方法"""
        self.__peek: ListNode | None = None
        self.__size: int = 0

    def size(self) -> int:
        """获取栈的长度"""
        return self.__size

    def is_empty(self) -> bool:
        """判断栈是否为空"""
        return not self.__peek

    def push(self, val: int) -> None:
        """入栈"""
        node = ListNode(val)
        node.next = self.__peek
        self.__peek = node
        self.__size += 1

    def pop(self) -> int:
        """出栈"""
        num: int = self.peek()
        self.__peek = self.__peek.next
        self.__size -= 1
        return num

    def peek(self) -> int:
        """访问栈顶元素"""
        # 判空处理
        if not self.__peek:
            return None
        return self.__peek.val

    def to_list(self) -> list[int]:
        """转化为列表用于打印"""
        arr: list[int] = []
        node = self.__peek
        while node:
            arr.append(node.val)
            node = node.next
        arr.reverse()
        return arr

linkedlist_stack.go

/* 基于链表实现的栈 */
type linkedListStack struct {
    // 使用内置包 list 来实现栈
    data *list.List
}

/* 初始化栈 */
func newLinkedListStack() *linkedListStack {
    return &linkedListStack{
        data: list.New(),
    }
}

/* 入栈 */
func (s *linkedListStack) push(value int) {
    s.data.PushBack(value)
}

/* 出栈 */
func (s *linkedListStack) pop() any {
    if s.isEmpty() {
        return nil
    }
    e := s.data.Back()
    s.data.Remove(e)
    return e.Value
}

/* 访问栈顶元素 */
func (s *linkedListStack) peek() any {
    if s.isEmpty() {
        return nil
    }
    e := s.data.Back()
    return e.Value
}

/* 获取栈的长度 */
func (s *linkedListStack) size() int {
    return s.data.Len()
}

/* 判断栈是否为空 */
func (s *linkedListStack) isEmpty() bool {
    return s.data.Len() == 0
}

/* 获取 List 用于打印 */
func (s *linkedListStack) toList() *list.List {
    return s.data
}

linkedlist_stack.js

/* 基于链表实现的栈 */
class LinkedListStack {
    #stackPeek;     // 将头节点作为栈顶
    #stkSize = 0;   // 栈的长度

    constructor() {
        this.#stackPeek = null;
    }

    /* 获取栈的长度 */
    get size() {
        return this.#stkSize;
    }

    /* 判断栈是否为空 */
    isEmpty() {
        return this.size == 0;
    }

    /* 入栈 */
    push(num) {
        const node = new ListNode(num);
        node.next = this.#stackPeek;
        this.#stackPeek = node;
        this.#stkSize++;
    }

    /* 出栈 */
    pop() {
        const num = this.peek();
        this.#stackPeek = this.#stackPeek.next;
        this.#stkSize--;
        return num;
    }

    /* 访问栈顶元素 */
    peek() {
        if (!this.#stackPeek)
            throw new Error("栈为空");
        return this.#stackPeek.val;
    }

    /* 将链表转化为 Array 并返回 */
    toArray() {
        let node = this.#stackPeek;
        const res = new Array(this.size);
        for (let i = res.length - 1; i >= 0; i--) {
            res[i] = node.val;
            node = node.next;
        }
        return res;
    }
}

linkedlist_stack.ts

/* 基于链表实现的栈 */
class LinkedListStack {
    private stackPeek: ListNode | null; // 将头节点作为栈顶
    private stkSize: number = 0; // 栈的长度

    constructor() {
        this.stackPeek = null;
    }

    /* 获取栈的长度 */
    get size(): number {
        return this.stkSize;
    }

    /* 判断栈是否为空 */
    isEmpty(): boolean {
        return this.size == 0;
    }

    /* 入栈 */
    push(num: number): void {
        const node = new ListNode(num);
        node.next = this.stackPeek;
        this.stackPeek = node;
        this.stkSize++;
    }

    /* 出栈 */
    pop(): number {
        const num = this.peek();
        if (!this.stackPeek) throw new Error('栈为空');
        this.stackPeek = this.stackPeek.next;
        this.stkSize--;
        return num;
    }

    /* 访问栈顶元素 */
    peek(): number {
        if (!this.stackPeek) throw new Error('栈为空');
        return this.stackPeek.val;
    }

    /* 将链表转化为 Array 并返回 */
    toArray(): number[] {
        let node = this.stackPeek;
        const res = new Array<number>(this.size);
        for (let i = res.length - 1; i >= 0; i--) {
            res[i] = node!.val;
            node = node!.next;
        }
        return res;
    }
}

linkedlist_stack.c

[class]{linkedListStack}-[func]{}

linkedlist_stack.cs

/* 基于链表实现的栈 */
class LinkedListStack
{
    private ListNode? stackPeek;  // 将头节点作为栈顶
    private int stkSize = 0;   // 栈的长度

    public LinkedListStack()
    {
        stackPeek = null;
    }

    /* 获取栈的长度 */
    public int size()
    {
        return stkSize;
    }

    /* 判断栈是否为空 */
    public bool isEmpty()
    {
        return size() == 0;
    }

    /* 入栈 */
    public void push(int num)
    {
        ListNode node = new ListNode(num);
        node.next = stackPeek;
        stackPeek = node;
        stkSize++;
    }

    /* 出栈 */
    public int pop()
    {
        if (stackPeek == null)
            throw new Exception();

        int num = peek();
        stackPeek = stackPeek.next;
        stkSize--;
        return num;
    }

    /* 访问栈顶元素 */
    public int peek()
    {
        if (size() == 0 || stackPeek == null)
            throw new Exception();
        return stackPeek.val;
    }

    /* 将 List 转化为 Array 并返回 */
    public int[] toArray()
    {
        if (stackPeek == null)
            return Array.Empty<int>();

        ListNode node = stackPeek;
        int[] res = new int[size()];
        for (int i = res.Length - 1; i >= 0; i--)
        {
            res[i] = node.val;
            node = node.next;
        }
        return res;
    }
}

linkedlist_stack.swift

/* 基于链表实现的栈 */
class LinkedListStack {
    private var _peek: ListNode? // 将头节点作为栈顶
    private var _size = 0 // 栈的长度

    init() {}

    /* 获取栈的长度 */
    func size() -> Int {
        _size
    }

    /* 判断栈是否为空 */
    func isEmpty() -> Bool {
        size() == 0
    }

    /* 入栈 */
    func push(num: Int) {
        let node = ListNode(x: num)
        node.next = _peek
        _peek = node
        _size += 1
    }

    /* 出栈 */
    @discardableResult
    func pop() -> Int {
        let num = peek()
        _peek = _peek?.next
        _size -= 1
        return num
    }

    /* 访问栈顶元素 */
    func peek() -> Int {
        if isEmpty() {
            fatalError("栈为空")
        }
        return _peek!.val
    }

    /* 将 List 转化为 Array 并返回 */
    func toArray() -> [Int] {
        var node = _peek
        var res = Array(repeating: 0, count: _size)
        for i in sequence(first: res.count - 1, next: { $0 >= 0 + 1 ? $0 - 1 : nil }) {
            res[i] = node!.val
            node = node?.next
        }
        return res
    }
}

linkedlist_stack.zig

// 基于链表实现的栈
fn LinkedListStack(comptime T: type) type {
    return struct {
        const Self = @This();

        stack_top: ?*inc.ListNode(T) = null,             // 将头节点作为栈顶
        stk_size: usize = 0,                             // 栈的长度
        mem_arena: ?std.heap.ArenaAllocator = null,
        mem_allocator: std.mem.Allocator = undefined,   // 内存分配器

        // 构造方法（分配内存+初始化栈）
        pub fn init(self: *Self, allocator: std.mem.Allocator) !void {
            if (self.mem_arena == null) {
                self.mem_arena = std.heap.ArenaAllocator.init(allocator);
                self.mem_allocator = self.mem_arena.?.allocator();
            }
            self.stack_top = null;
            self.stk_size = 0;
        }

        // 析构方法（释放内存）
        pub fn deinit(self: *Self) void {
            if (self.mem_arena == null) return;
            self.mem_arena.?.deinit();
        }

        // 获取栈的长度
        pub fn size(self: *Self) usize {
            return self.stk_size;
        }

        // 判断栈是否为空
        pub fn isEmpty(self: *Self) bool {
            return self.size() == 0;
        }

        // 访问栈顶元素
        pub fn peek(self: *Self) T {
            if (self.size() == 0) @panic("栈为空");
            return self.stack_top.?.val;
        }  

        // 入栈
        pub fn push(self: *Self, num: T) !void {
            var node = try self.mem_allocator.create(inc.ListNode(T));
            node.init(num);
            node.next = self.stack_top;
            self.stack_top = node;
            self.stk_size += 1;
        } 

        // 出栈
        pub fn pop(self: *Self) T {
            var num = self.peek();
            self.stack_top = self.stack_top.?.next;
            self.stk_size -= 1;
            return num;
        } 

        // 将栈转换为数组
        pub fn toArray(self: *Self) ![]T {
            var node = self.stack_top;
            var res = try self.mem_allocator.alloc(T, self.size());
            std.mem.set(T, res, @as(T, 0));
            var i: usize = 0;
            while (i < res.len) : (i += 1) {
                res[res.len - i - 1] = node.?.val;
                node = node.?.next;
            }
            return res;
        }
    };
}

基于数组的实现

在基于「数组」实现栈时，我们可以将数组的尾部作为栈顶。在这样的设计下，入栈与出栈操作就分别对应在数组尾部添加元素与删除元素，时间复杂度都为 \(O(1)\) 。

ArrayStackpush()pop()

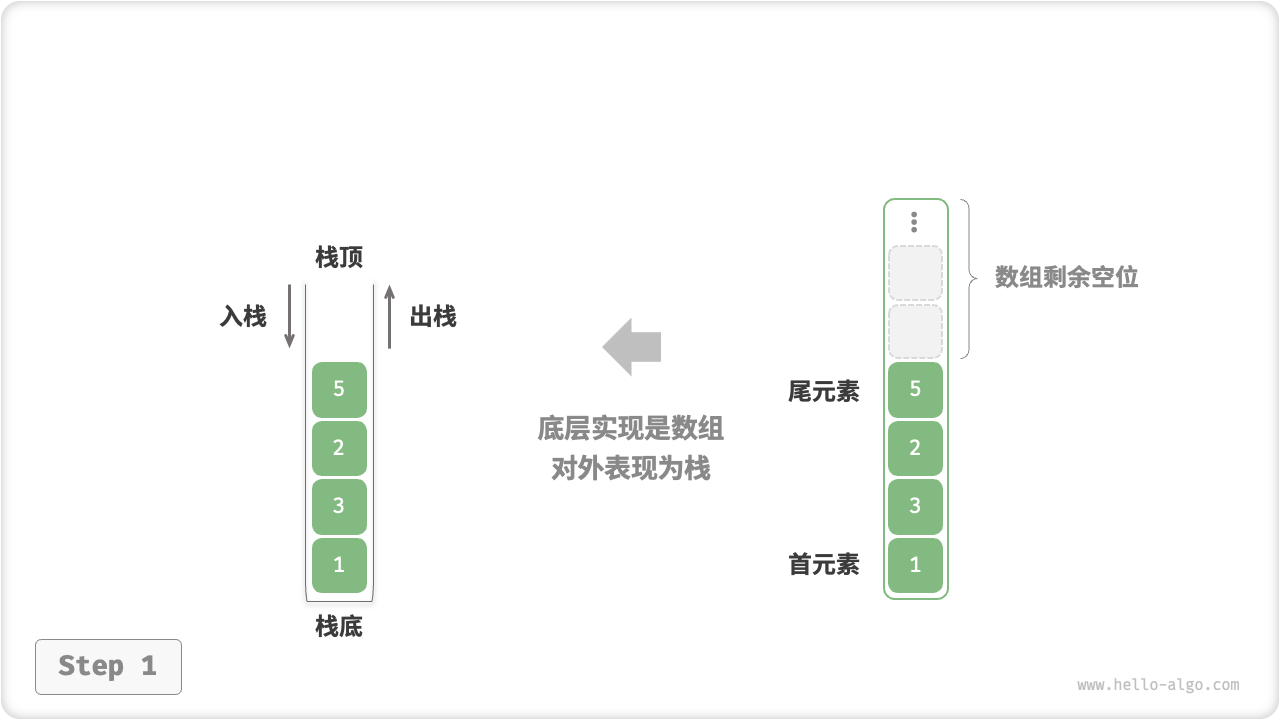
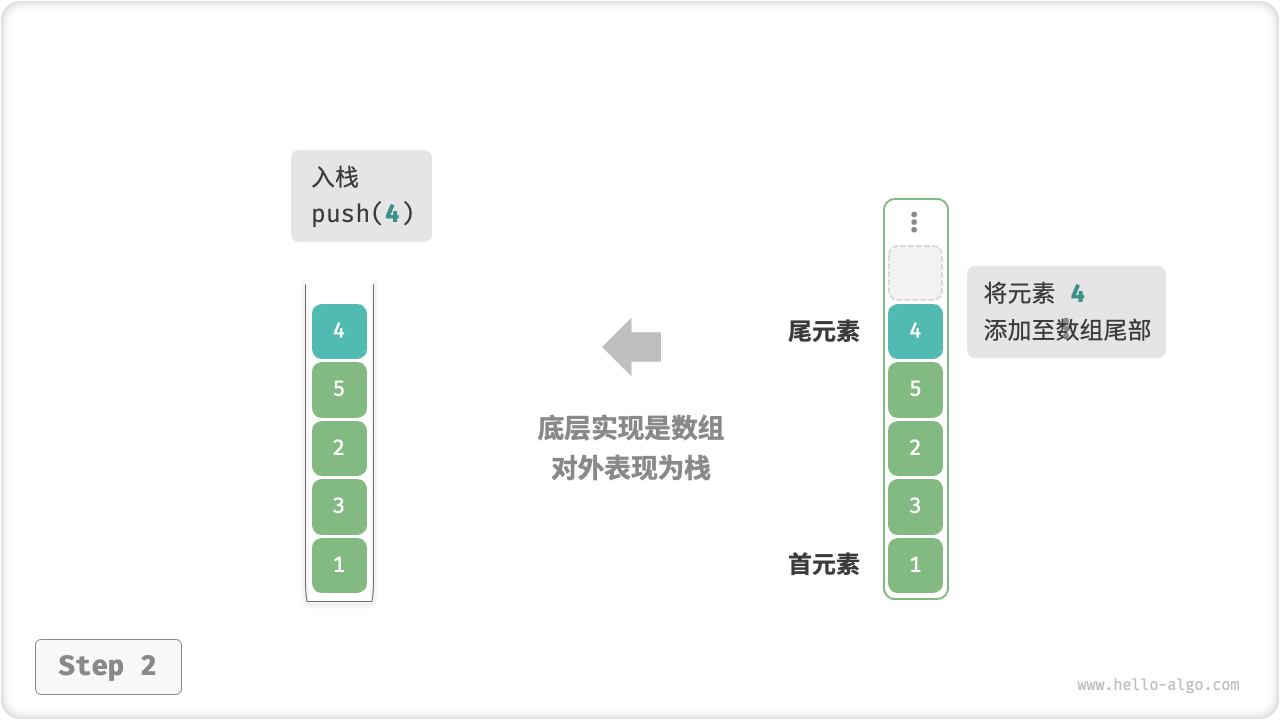
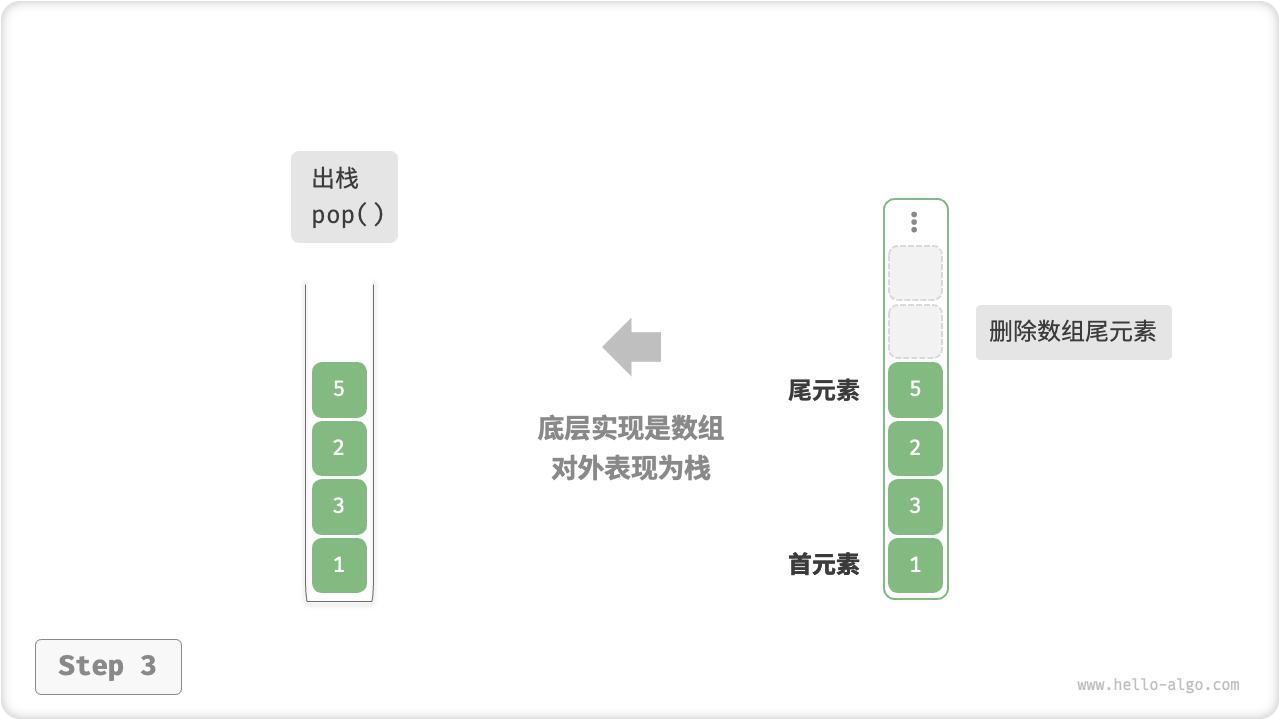
由于入栈的元素可能会源源不断地增加，因此我们可以使用动态数组，这样就无需自行处理数组扩容问题。以下为示例代码。

JavaC++PythonGoJavaScriptTypeScriptCC#SwiftZig

array_stack.java

/* 基于数组实现的栈 */
class ArrayStack {
    private ArrayList<Integer> stack;

    public ArrayStack() {
        // 初始化列表（动态数组）
        stack = new ArrayList<>();
    }

    /* 获取栈的长度 */
    public int size() {
        return stack.size();
    }

    /* 判断栈是否为空 */
    public boolean isEmpty() {
        return size() == 0;
    }

    /* 入栈 */
    public void push(int num) {
        stack.add(num);
    }

    /* 出栈 */
    public int pop() {
        if (isEmpty())
            throw new EmptyStackException();
        return stack.remove(size() - 1);
    }

    /* 访问栈顶元素 */
    public int peek() {
        if (isEmpty())
            throw new EmptyStackException();
        return stack.get(size() - 1);
    }

    /* 将 List 转化为 Array 并返回 */
    public Object[] toArray() {
        return stack.toArray();
    }
}

array_stack.cpp

/* 基于数组实现的栈 */
class ArrayStack {
  private:
    vector<int> stack;

  public:
    /* 获取栈的长度 */
    int size() {
        return stack.size();
    }

    /* 判断栈是否为空 */
    bool empty() {
        return stack.empty();
    }

    /* 入栈 */
    void push(int num) {
        stack.push_back(num);
    }

    /* 出栈 */
    void pop() {
        int oldTop = top();
        stack.pop_back();
    }

    /* 访问栈顶元素 */
    int top() {
        if (empty())
            throw out_of_range("栈为空");
        return stack.back();
    }

    /* 返回 Vector */
    vector<int> toVector() {
        return stack;
    }
};

array_stack.py

class ArrayStack:
    """基于数组实现的栈"""

    def __init__(self) -> None:
        """构造方法"""
        self.__stack: list[int] = []

    def size(self) -> int:
        """获取栈的长度"""
        return len(self.__stack)

    def is_empty(self) -> bool:
        """判断栈是否为空"""
        return self.__stack == []

    def push(self, item: int) -> None:
        """入栈"""
        self.__stack.append(item)

    def pop(self) -> int:
        """出栈"""
        assert not self.is_empty(), "栈为空"
        return self.__stack.pop()

    def peek(self) -> int:
        """访问栈顶元素"""
        assert not self.is_empty(), "栈为空"
        return self.__stack[-1]

    def to_list(self) -> list[int]:
        """返回列表用于打印"""
        return self.__stack

array_stack.go

/* 基于数组实现的栈 */
type arrayStack struct {
    data []int // 数据
}

/* 初始化栈 */
func newArrayStack() *arrayStack {
    return &arrayStack{
        // 设置栈的长度为 0，容量为 16
        data: make([]int, 0, 16),
    }
}

/* 栈的长度 */
func (s *arrayStack) size() int {
    return len(s.data)
}

/* 栈是否为空 */
func (s *arrayStack) isEmpty() bool {
    return s.size() == 0
}

/* 入栈 */
func (s *arrayStack) push(v int) {
    // 切片会自动扩容
    s.data = append(s.data, v)
}

/* 出栈 */
func (s *arrayStack) pop() any {
    val := s.peek()
    s.data = s.data[:len(s.data)-1]
    return val
}

/* 获取栈顶元素 */
func (s *arrayStack) peek() any {
    if s.isEmpty() {
        return nil
    }
    val := s.data[len(s.data)-1]
    return val
}

/* 获取 Slice 用于打印 */
func (s *arrayStack) toSlice() []int {
    return s.data
}

array_stack.js

/* 基于数组实现的栈 */
class ArrayStack {
    #stack;
    constructor() {
        this.#stack = [];
    }

    /* 获取栈的长度 */
    get size() {
        return this.#stack.length;
    }

    /* 判断栈是否为空 */
    empty() {
        return this.#stack.length === 0;
    }

    /* 入栈 */
    push(num) {
        this.#stack.push(num);
    }

    /* 出栈 */
    pop() {
        if (this.empty())
            throw new Error("栈为空");
        return this.#stack.pop();
    }

    /* 访问栈顶元素 */
    top() {
        if (this.empty())
            throw new Error("栈为空");
        return this.#stack[this.#stack.length - 1];
    }

    /* 返回 Array */
    toArray() {
        return this.#stack;
    }
};

array_stack.ts

/* 基于数组实现的栈 */
class ArrayStack {
    private stack: number[];
    constructor() {
        this.stack = [];
    }

    /* 获取栈的长度 */
    get size(): number {
        return this.stack.length;
    }

    /* 判断栈是否为空 */
    empty(): boolean {
        return this.stack.length === 0;
    }

    /* 入栈 */
    push(num: number): void {
        this.stack.push(num);
    }

    /* 出栈 */
    pop(): number | undefined {
        if (this.empty())
            throw new Error('栈为空');
        return this.stack.pop();
    }

    /* 访问栈顶元素 */
    top(): number | undefined {
        if (this.empty())
            throw new Error('栈为空');
        return this.stack[this.stack.length - 1];
    }

    /* 返回 Array */
    toArray() {
        return this.stack;
    }
};

array_stack.c

[class]{arrayStack}-[func]{}

array_stack.cs

/* 基于数组实现的栈 */
class ArrayStack
{
    private List<int> stack;
    public ArrayStack()
    {
        // 初始化列表（动态数组）
        stack = new();
    }

    /* 获取栈的长度 */
    public int size()
    {
        return stack.Count();
    }

    /* 判断栈是否为空 */
    public bool isEmpty()
    {
        return size() == 0;
    }

    /* 入栈 */
    public void push(int num)
    {
        stack.Add(num);
    }

    /* 出栈 */
    public int pop()
    {
        if (isEmpty())
            throw new Exception();
        var val = peek();
        stack.RemoveAt(size() - 1);
        return val;
    }

    /* 访问栈顶元素 */
    public int peek()
    {
        if (isEmpty())
            throw new Exception();
        return stack[size() - 1];
    }

    /* 将 List 转化为 Array 并返回 */
    public int[] toArray()
    {
        return stack.ToArray();
    }
}

array_stack.swift

/* 基于数组实现的栈 */
class ArrayStack {
    private var stack: [Int]

    init() {
        // 初始化列表（动态数组）
        stack = []
    }

    /* 获取栈的长度 */
    func size() -> Int {
        stack.count
    }

    /* 判断栈是否为空 */
    func isEmpty() -> Bool {
        stack.isEmpty
    }

    /* 入栈 */
    func push(num: Int) {
        stack.append(num)
    }

    /* 出栈 */
    @discardableResult
    func pop() -> Int {
        if isEmpty() {
            fatalError("栈为空")
        }
        return stack.removeLast()
    }

    /* 访问栈顶元素 */
    func peek() -> Int {
        if isEmpty() {
            fatalError("栈为空")
        }
        return stack.last!
    }

    /* 将 List 转化为 Array 并返回 */
    func toArray() -> [Int] {
        stack
    }
}

array_stack.zig

// 基于数组实现的栈
fn ArrayStack(comptime T: type) type {
    return struct {
        const Self = @This();

        stack: ?std.ArrayList(T) = null,     

        // 构造方法（分配内存+初始化栈）
        pub fn init(self: *Self, allocator: std.mem.Allocator) void {
            if (self.stack == null) {
                self.stack = std.ArrayList(T).init(allocator);
            }
        }

        // 析构方法（释放内存）
        pub fn deinit(self: *Self) void {
            if (self.stack == null) return;
            self.stack.?.deinit();
        }

        // 获取栈的长度
        pub fn size(self: *Self) usize {
            return self.stack.?.items.len;
        }

        // 判断栈是否为空
        pub fn isEmpty(self: *Self) bool {
            return self.size() == 0;
        }

        // 访问栈顶元素
        pub fn peek(self: *Self) T {
            if (self.isEmpty()) @panic("栈为空");
            return self.stack.?.items[self.size() - 1];
        }  

        // 入栈
        pub fn push(self: *Self, num: T) !void {
            try self.stack.?.append(num);
        } 

        // 出栈
        pub fn pop(self: *Self) T {
            var num = self.stack.?.pop();
            return num;
        } 

        // 返回 ArrayList
        pub fn toList(self: *Self) std.ArrayList(T) {
            return self.stack.?;
        }
    };
}

5.1.3.   两种实现对比

支持操作

两种实现都支持栈定义中的各项操作。数组实现额外支持随机访问，但这已超出了栈的定义范畴，因此一般不会用到。

时间效率

在基于数组的实现中，入栈和出栈操作都是在预先分配好的连续内存中进行，具有很好的缓存本地性，因此效率较高。然而，如果入栈时超出数组容量，会触发扩容机制，导致该次入栈操作的时间复杂度变为 \(O(n)\) 。

在链表实现中，链表的扩容非常灵活，不存在上述数组扩容时效率降低的问题。但是，入栈操作需要初始化节点对象并修改指针，因此效率相对较低。不过，如果入栈元素本身就是节点对象，那么可以省去初始化步骤，从而提高效率。

综上所述，当入栈与出栈操作的元素是基本数据类型（如 int , double ）时，我们可以得出以下结论：

• 基于数组实现的栈在触发扩容时效率会降低，但由于扩容是低频操作，因此平均效率更高；
• 基于链表实现的栈可以提供更加稳定的效率表现；

空间效率

在初始化列表时，系统会为列表分配“初始容量”，该容量可能超过实际需求。并且，扩容机制通常是按照特定倍率（例如 2 倍）进行扩容，扩容后的容量也可能超出实际需求。因此，基于数组实现的栈可能造成一定的空间浪费。

然而，由于链表节点需要额外存储指针，因此链表节点占用的空间相对较大。

综上，我们不能简单地确定哪种实现更加节省内存，需要针对具体情况进行分析。

5.1.4.   栈典型应用

• 浏览器中的后退与前进、软件中的撤销与反撤销。每当我们打开新的网页，浏览器就会将上一个网页执行入栈，这样我们就可以通过「后退」操作回到上一页面。后退操作实际上是在执行出栈。如果要同时支持后退和前进，那么需要两个栈来配合实现。
• 程序内存管理。每次调用函数时，系统都会在栈顶添加一个栈帧，用于记录函数的上下文信息。在递归函数中，向下递推阶段会不断执行入栈操作，而向上回溯阶段则会执行出栈操作。

评论