13.2. 全排列问题¶
全排列问题是回溯算法的一个典型应用。它的定义是在给定一个集合（如一个数组或字符串）的情况下，找出这个集合中元素的所有可能的排列。
如下表所示，列举了几个示例数组和其对应的所有排列。
| 输入数组 | 所有排列 |
|---|---|
| \([1]\) | \([1]\) |
| \([1, 2]\) | \([1, 2], [2, 1]\) |
| \([1, 2, 3]\) | \([1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2], [3, 2, 1]\) |
13.2.1. 无重复的情况¶
输入一个整数数组，数组中不包含重复元素，返回所有可能的排列。
从回溯算法的角度看，我们可以把生成排列的过程想象成一系列选择的结果。假设输入数组为 \([1, 2, 3]\) ，如果我们先选择 \(1\) 、再选择 \(3\) 、最后选择 \(2\) ，则获得排列 \([1, 3, 2]\) 。回退表示撤销一个选择，之后继续尝试其他选择。
从回溯算法代码的角度看，候选集合 choices 是输入数组中的所有元素，状态 state 是直至目前已被选择的元素。注意，每个元素只允许被选择一次，因此在遍历选择时，应当排除已经选择过的元素。
如下图所示，我们可以将搜索过程展开成一个递归树，树中的每个节点代表当前状态 state 。从根节点开始，经过三轮选择后到达叶节点，每个叶节点都对应一个排列。
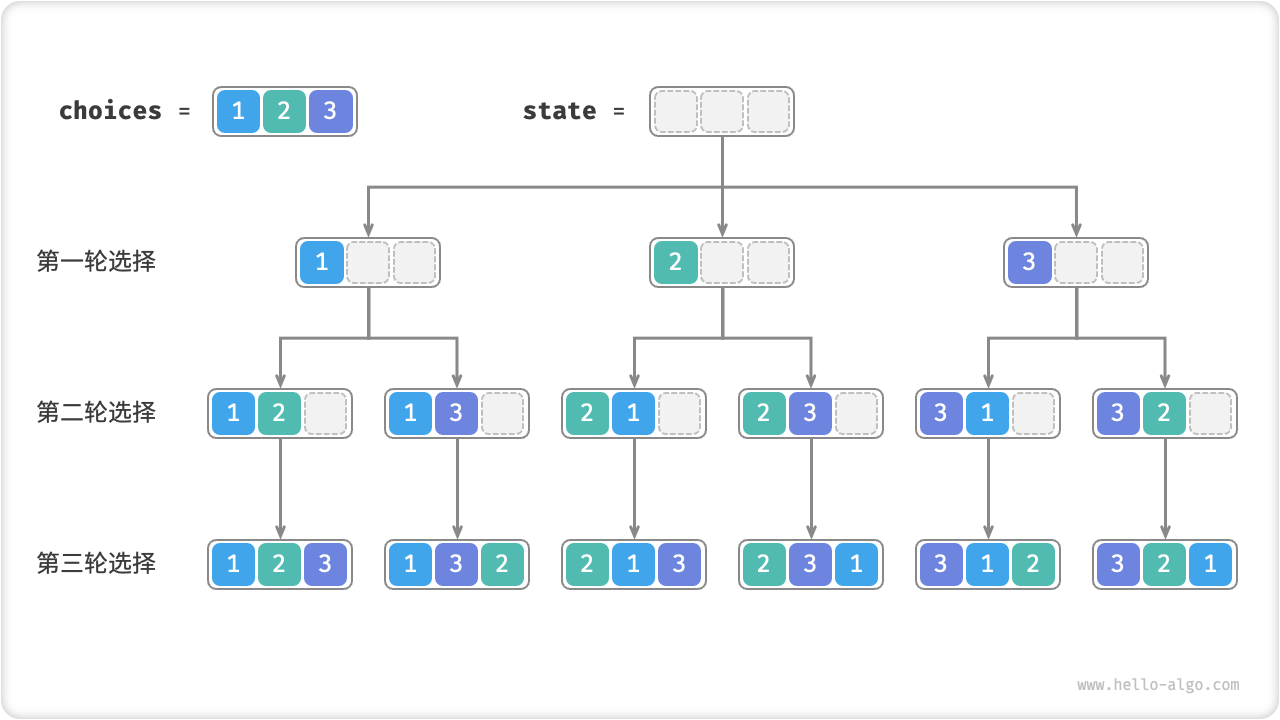
Fig. 全排列的递归树
想清楚以上信息之后，我们就可以在框架代码中做“完形填空”了。为了缩短代码行数，我们不单独实现框架代码中的各个函数，而是将他们展开在 backtrack() 函数中。
permutations_i.java
/* 回溯算法：全排列 I */
void backtrack(List<Integer> state, int[] choices, boolean[] selected, List<List<Integer>> res) {
// 当状态长度等于元素数量时，记录解
if (state.size() == choices.length) {
res.add(new ArrayList<Integer>(state));
return;
}
// 遍历所有选择
for (int i = 0; i < choices.length; i++) {
int choice = choices[i];
// 剪枝：不允许重复选择元素 且 不允许重复选择相等元素
if (!selected[i]) {
// 尝试：做出选择，更新状态
selected[i] = true;
state.add(choice);
// 进行下一轮选择
backtrack(state, choices, selected, res);
// 回退：撤销选择，恢复到之前的状态
selected[i] = false;
state.remove(state.size() - 1);
}
}
}
/* 全排列 I */
List<List<Integer>> permutationsI(int[] nums) {
List<List<Integer>> res = new ArrayList<List<Integer>>();
backtrack(new ArrayList<Integer>(), nums, new boolean[nums.length], res);
return res;
}
permutations_i.cpp
/* 回溯算法：全排列 I */
void backtrack(vector<int> &state, const vector<int> &choices, vector<bool> &selected, vector<vector<int>> &res) {
// 当状态长度等于元素数量时，记录解
if (state.size() == choices.size()) {
res.push_back(state);
return;
}
// 遍历所有选择
for (int i = 0; i < choices.size(); i++) {
int choice = choices[i];
// 剪枝：不允许重复选择元素 且 不允许重复选择相等元素
if (!selected[i]) {
// 尝试：做出选择，更新状态
selected[i] = true;
state.push_back(choice);
// 进行下一轮选择
backtrack(state, choices, selected, res);
// 回退：撤销选择，恢复到之前的状态
selected[i] = false;
state.pop_back();
}
}
}
/* 全排列 I */
vector<vector<int>> permutationsI(vector<int> nums) {
vector<int> state;
vector<bool> selected(nums.size(), false);
vector<vector<int>> res;
backtrack(state, nums, selected, res);
return res;
}
permutations_i.py
def backtrack(
state: list[int], choices: list[int], selected: list[bool], res: list[list[int]]
):
"""回溯算法：全排列 I"""
# 当状态长度等于元素数量时，记录解
if len(state) == len(choices):
res.append(list(state))
return
# 遍历所有选择
for i, choice in enumerate(choices):
# 剪枝：不允许重复选择元素
if not selected[i]:
# 尝试：做出选择，更新状态
selected[i] = True
state.append(choice)
# 进行下一轮选择
backtrack(state, choices, selected, res)
# 回退：撤销选择，恢复到之前的状态
selected[i] = False
state.pop()
def permutations_i(nums: list[int]) -> list[list[int]]:
"""全排列 I"""
res = []
backtrack(state=[], choices=nums, selected=[False] * len(nums), res=res)
return res
permutations_i.cs
/* 回溯算法：全排列 I */
void backtrack(List<int> state, int[] choices, bool[] selected, List<List<int>> res) {
// 当状态长度等于元素数量时，记录解
if (state.Count == choices.Length) {
res.Add(new List<int>(state));
return;
}
// 遍历所有选择
for (int i = 0; i < choices.Length; i++) {
int choice = choices[i];
// 剪枝：不允许重复选择元素 且 不允许重复选择相等元素
if (!selected[i]) {
// 尝试：做出选择，更新状态
selected[i] = true;
state.Add(choice);
// 进行下一轮选择
backtrack(state, choices, selected, res);
// 回退：撤销选择，恢复到之前的状态
selected[i] = false;
state.RemoveAt(state.Count - 1);
}
}
}
/* 全排列 I */
List<List<int>> permutationsI(int[] nums) {
List<List<int>> res = new List<List<int>>();
backtrack(new List<int>(), nums, new bool[nums.Length], res);
return res;
}
permutations_i.swift
/* 回溯算法：全排列 I */
func backtrack(state: inout [Int], choices: [Int], selected: inout [Bool], res: inout [[Int]]) {
// 当状态长度等于元素数量时，记录解
if state.count == choices.count {
res.append(state)
return
}
// 遍历所有选择
for (i, choice) in choices.enumerated() {
// 剪枝：不允许重复选择元素 且 不允许重复选择相等元素
if !selected[i] {
// 尝试：做出选择，更新状态
selected[i] = true
state.append(choice)
// 进行下一轮选择
backtrack(state: &state, choices: choices, selected: &selected, res: &res)
// 回退：撤销选择，恢复到之前的状态
selected[i] = false
state.removeLast()
}
}
}
/* 全排列 I */
func permutationsI(nums: [Int]) -> [[Int]] {
var state: [Int] = []
var selected = Array(repeating: false, count: nums.count)
var res: [[Int]] = []
backtrack(state: &state, choices: nums, selected: &selected, res: &res)
return res
}
需要重点关注的是，我们引入了一个布尔型数组 selected ，它的长度与输入数组长度相等，其中 selected[i] 表示 choices[i] 是否已被选择。我们利用 selected 避免某个元素被重复选择，从而实现剪枝。
如下图所示，假设我们第一轮选择 1 ，第二轮选择 3 ，第三轮选择 2 ，则需要在第二轮剪掉元素 1 的分支，在第三轮剪掉元素 1, 3 的分支。从本质上理解，此剪枝操作可将搜索空间大小从 \(O(n^n)\) 降低至 \(O(n!)\) 。
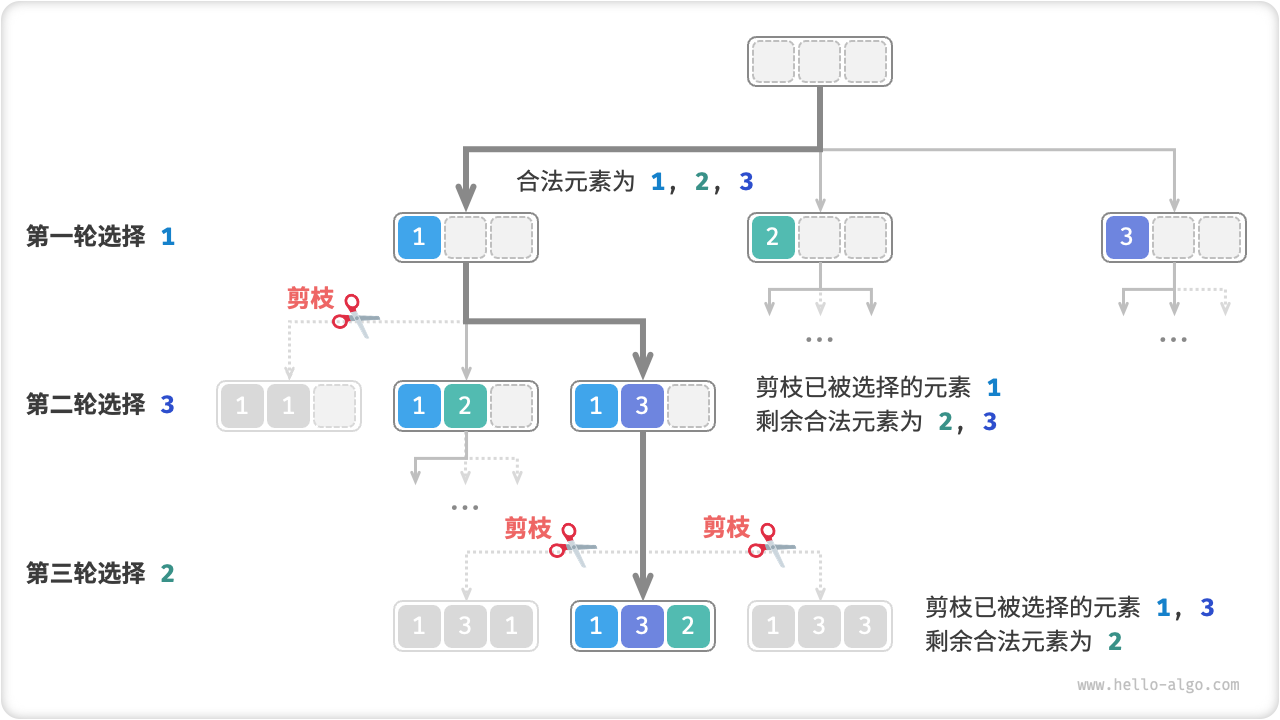
Fig. 全排列剪枝示例
13.2.2. 考虑重复的情况¶
输入一个整数数组，数组中可能包含重复元素，返回所有不重复的排列。
假设输入数组为 \([1, 1, 2]\) 。为了方便区分两个重复的元素 \(1\) ，接下来我们将第二个元素记为 \(\hat{1}\) 。如下图所示，上述方法生成的排列有一半都是重复的。
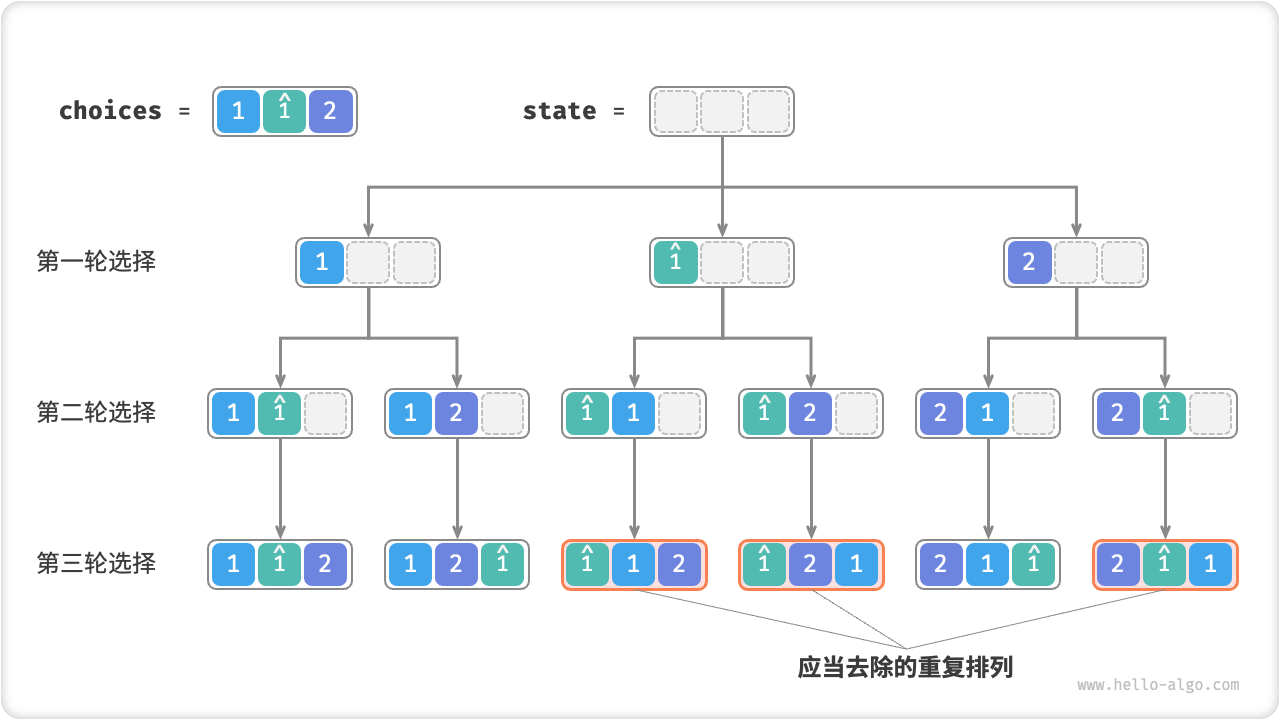
Fig. 重复排列
那么，如何去除重复的排列呢？最直接地，我们可以借助一个哈希表，直接对排列结果进行去重。然而，这样做不够优雅，因为生成重复排列的搜索分支是没有必要的，应当被提前识别并剪枝，这样可以提升算法效率。
观察发现，在第一轮中，选择 \(1\) 或选择 \(\hat{1}\) 是等价的，因为在这两个选择之下生成的所有排列都是重复的。因此，我们应该把 \(\hat{1}\) 剪枝掉。同理，在第一轮选择 \(2\) 后，第二轮选择中的 \(1\) 和 \(\hat{1}\) 也会产生重复分支，因此也需要将第二轮的 \(\hat{1}\) 剪枝。
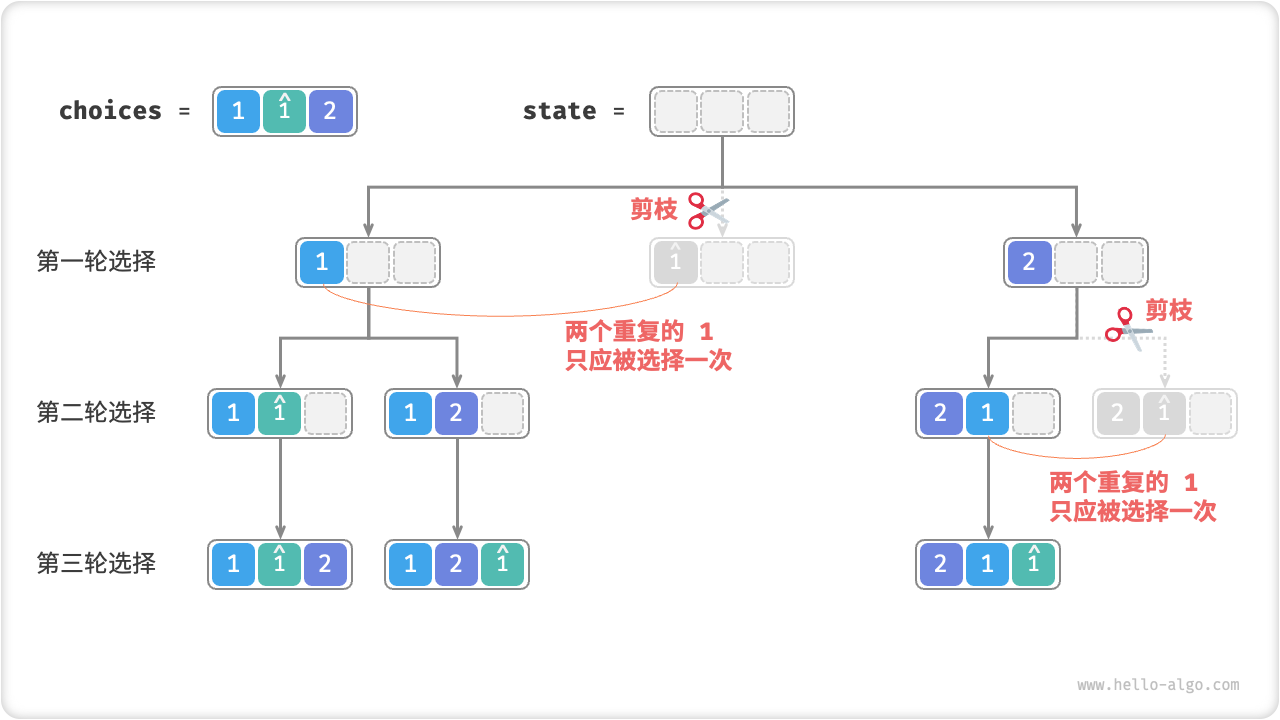
Fig. 重复排列剪枝
本质上看，我们的目标是实现在某一轮选择中，多个相等的元素仅被选择一次。因此，在上一题的代码的基础上，我们考虑在每一轮选择中开启一个哈希表 duplicated ，用于记录该轮中已经尝试过的元素，并将重复元素剪枝。
permutations_ii.java
/* 回溯算法：全排列 II */
void backtrack(List<Integer> state, int[] choices, boolean[] selected, List<List<Integer>> res) {
// 当状态长度等于元素数量时，记录解
if (state.size() == choices.length) {
res.add(new ArrayList<Integer>(state));
return;
}
// 遍历所有选择
Set<Integer> duplicated = new HashSet<Integer>();
for (int i = 0; i < choices.length; i++) {
int choice = choices[i];
// 剪枝：不允许重复选择元素 且 不允许重复选择相等元素
if (!selected[i] && !duplicated.contains(choice)) {
// 尝试：做出选择，更新状态
duplicated.add(choice); // 记录选择过的元素值
selected[i] = true;
state.add(choice);
// 进行下一轮选择
backtrack(state, choices, selected, res);
// 回退：撤销选择，恢复到之前的状态
selected[i] = false;
state.remove(state.size() - 1);
}
}
}
/* 全排列 II */
List<List<Integer>> permutationsII(int[] nums) {
List<List<Integer>> res = new ArrayList<List<Integer>>();
backtrack(new ArrayList<Integer>(), nums, new boolean[nums.length], res);
return res;
}
permutations_ii.cpp
/* 回溯算法：全排列 II */
void backtrack(vector<int> &state, const vector<int> &choices, vector<bool> &selected, vector<vector<int>> &res) {
// 当状态长度等于元素数量时，记录解
if (state.size() == choices.size()) {
res.push_back(state);
return;
}
// 遍历所有选择
unordered_set<int> duplicated;
for (int i = 0; i < choices.size(); i++) {
int choice = choices[i];
// 剪枝：不允许重复选择元素 且 不允许重复选择相等元素
if (!selected[i] && duplicated.find(choice) == duplicated.end()) {
// 尝试：做出选择，更新状态
duplicated.emplace(choice); // 记录选择过的元素值
selected[i] = true;
state.push_back(choice);
// 进行下一轮选择
backtrack(state, choices, selected, res);
// 回退：撤销选择，恢复到之前的状态
selected[i] = false;
state.pop_back();
}
}
}
/* 全排列 II */
vector<vector<int>> permutationsII(vector<int> nums) {
vector<int> state;
vector<bool> selected(nums.size(), false);
vector<vector<int>> res;
backtrack(state, nums, selected, res);
return res;
}
permutations_ii.py
def backtrack(
state: list[int], choices: list[int], selected: list[bool], res: list[list[int]]
):
"""回溯算法：全排列 II"""
# 当状态长度等于元素数量时，记录解
if len(state) == len(choices):
res.append(list(state))
return
# 遍历所有选择
duplicated = set[int]()
for i, choice in enumerate(choices):
# 剪枝：不允许重复选择元素 且 不允许重复选择相等元素
if not selected[i] and choice not in duplicated:
# 尝试：做出选择，更新状态
duplicated.add(choice) # 记录选择过的元素值
selected[i] = True
state.append(choice)
# 进行下一轮选择
backtrack(state, choices, selected, res)
# 回退：撤销选择，恢复到之前的状态
selected[i] = False
state.pop()
def permutations_ii(nums: list[int]) -> list[list[int]]:
"""全排列 II"""
res = []
backtrack(state=[], choices=nums, selected=[False] * len(nums), res=res)
return res
permutations_ii.cs
/* 回溯算法：全排列 II */
void backtrack(List<int> state, int[] choices, bool[] selected, List<List<int>> res) {
// 当状态长度等于元素数量时，记录解
if (state.Count == choices.Length) {
res.Add(new List<int>(state));
return;
}
// 遍历所有选择
ISet<int> duplicated = new HashSet<int>();
for (int i = 0; i < choices.Length; i++) {
int choice = choices[i];
// 剪枝：不允许重复选择元素 且 不允许重复选择相等元素
if (!selected[i] && !duplicated.Contains(choice)) {
// 尝试：做出选择，更新状态
duplicated.Add(choice); // 记录选择过的元素值
selected[i] = true;
state.Add(choice);
// 进行下一轮选择
backtrack(state, choices, selected, res);
// 回退：撤销选择，恢复到之前的状态
selected[i] = false;
state.RemoveAt(state.Count - 1);
}
}
}
/* 全排列 II */
List<List<int>> permutationsII(int[] nums) {
List<List<int>> res = new List<List<int>>();
backtrack(new List<int>(), nums, new bool[nums.Length], res);
return res;
}
permutations_ii.swift
/* 回溯算法：全排列 II */
func backtrack(state: inout [Int], choices: [Int], selected: inout [Bool], res: inout [[Int]]) {
// 当状态长度等于元素数量时，记录解
if state.count == choices.count {
res.append(state)
return
}
// 遍历所有选择
var duplicated: Set<Int> = []
for (i, choice) in choices.enumerated() {
// 剪枝：不允许重复选择元素 且 不允许重复选择相等元素
if !selected[i], !duplicated.contains(choice) {
// 尝试：做出选择，更新状态
duplicated.insert(choice) // 记录选择过的元素值
selected[i] = true
state.append(choice)
// 进行下一轮选择
backtrack(state: &state, choices: choices, selected: &selected, res: &res)
// 回退：撤销选择，恢复到之前的状态
selected[i] = false
state.removeLast()
}
}
}
/* 全排列 II */
func permutationsII(nums: [Int]) -> [[Int]] {
var state: [Int] = []
var selected = Array(repeating: false, count: nums.count)
var res: [[Int]] = []
backtrack(state: &state, choices: nums, selected: &selected, res: &res)
return res
}
注意，虽然 selected 和 duplicated 都起到剪枝的作用，但他们剪掉的是不同的分支：
- 剪枝条件一：整个搜索过程中只有一个
selected。它记录的是当前状态中包含哪些元素，作用是避免某个元素在state中重复出现。 - 剪枝条件二：每轮选择（即每个开启的
backtrack函数）都包含一个duplicated。它记录的是在遍历中哪些元素已被选择过，作用是保证相等元素只被选择一次，以避免产生重复的搜索分支。
下图展示了两个剪枝条件的生效范围。注意，树中的每个节点代表一个选择，从根节点到叶节点的路径上的各个节点构成一个排列。
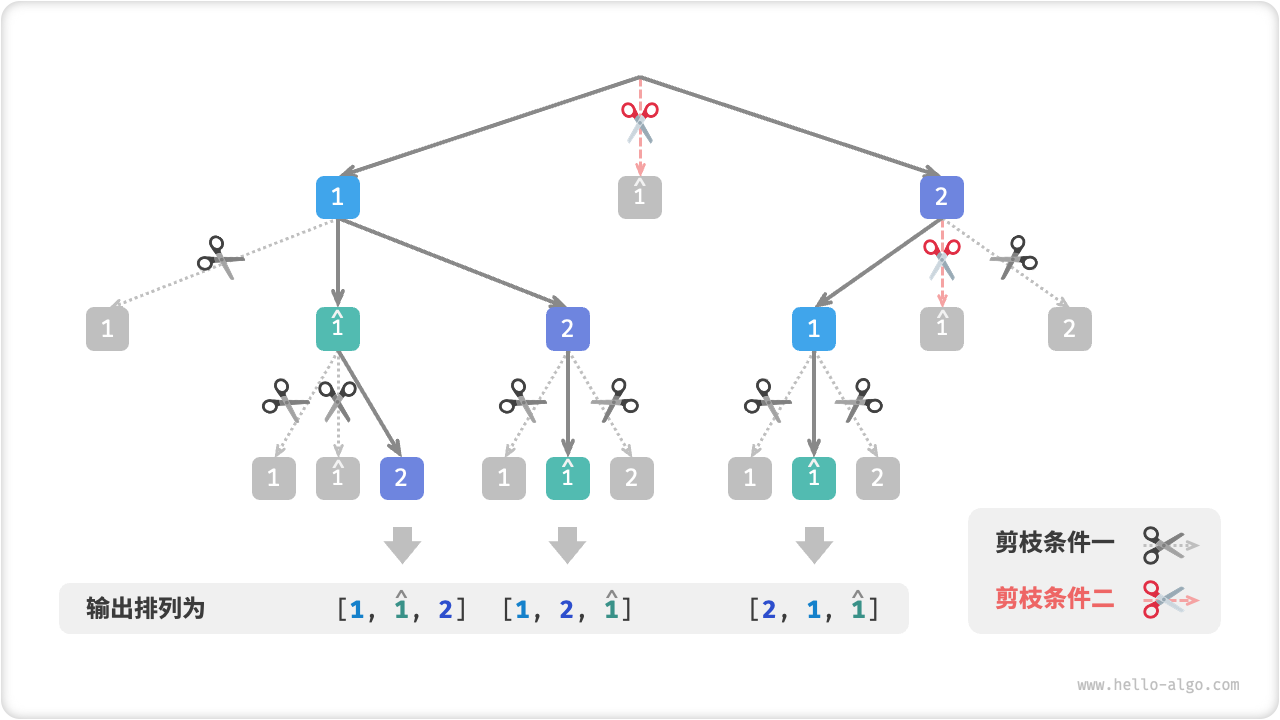
Fig. 两种剪枝条件的作用范围
13.2.3. 复杂度分析¶
假设元素两两之间互不相同，则 \(n\) 个元素共有 \(n!\) 种排列（阶乘）；在记录结果时，需要复制长度为 \(n\) 的列表，使用 \(O(n)\) 时间。因此，时间复杂度为 \(O(n!n)\) 。
最大递归深度为 \(n\) ，使用 \(O(n)\) 栈帧空间。selected 使用 \(O(n)\) 空间。同一时刻最多共有 \(n\) 个 duplicated ，使用 \(O(n^2)\) 空间。因此，全排列 I 的空间复杂度为 \(O(n)\) ，全排列 II 的空间复杂度为 \(O(n^2)\) 。