跳轉至

8.2   建堆積操作

在某些情況下，我們希望使用一個串列的所有元素來構建一個堆積，這個過程被稱為“建堆積操作”。

8.2.1   藉助入堆積操作實現

我們首先建立一個空堆積，然後走訪串列，依次對每個元素執行“入堆積操作”，即先將元素新增至堆積的尾部，再對該元素執行“從底至頂”堆積化。

每當一個元素入堆積，堆積的長度就加一。由於節點是從頂到底依次被新增進二元樹的，因此堆積是“自上而下”構建的。

設元素數量為 \(n\) ，每個元素的入堆積操作使用 \(O(\log{n})\) 時間，因此該建堆積方法的時間複雜度為 \(O(n \log n)\) 。

8.2.2   透過走訪堆積化實現

實際上，我們可以實現一種更為高效的建堆積方法，共分為兩步。

  1. 將串列所有元素原封不動地新增到堆積中，此時堆積的性質尚未得到滿足。
  2. 倒序走訪堆積（層序走訪的倒序），依次對每個非葉節點執行“從頂至底堆積化”。

每當堆積化一個節點後，以該節點為根節點的子樹就形成一個合法的子堆積。而由於是倒序走訪，因此堆積是“自下而上”構建的。

之所以選擇倒序走訪，是因為這樣能夠保證當前節點之下的子樹已經是合法的子堆積，這樣堆積化當前節點才是有效的。

值得說明的是，由於葉節點沒有子節點，因此它們天然就是合法的子堆積，無須堆積化。如以下程式碼所示，最後一個非葉節點是最後一個節點的父節點，我們從它開始倒序走訪並執行堆積化：

my_heap.py
def __init__(self, nums: list[int]):
    """建構子，根據輸入串列建堆積"""
    # 將串列元素原封不動新增進堆積
    self.max_heap = nums
    # 堆積化除葉節點以外的其他所有節點
    for i in range(self.parent(self.size() - 1), -1, -1):
        self.sift_down(i)
my_heap.cpp
/* 建構子，根據輸入串列建堆積 */
MaxHeap(vector<int> nums) {
    // 將串列元素原封不動新增進堆積
    maxHeap = nums;
    // 堆積化除葉節點以外的其他所有節點
    for (int i = parent(size() - 1); i >= 0; i--) {
        siftDown(i);
    }
}
my_heap.java
/* 建構子，根據輸入串列建堆積 */
MaxHeap(List<Integer> nums) {
    // 將串列元素原封不動新增進堆積
    maxHeap = new ArrayList<>(nums);
    // 堆積化除葉節點以外的其他所有節點
    for (int i = parent(size() - 1); i >= 0; i--) {
        siftDown(i);
    }
}
my_heap.cs
/* 建構子，根據輸入串列建堆積 */
MaxHeap(IEnumerable<int> nums) {
    // 將串列元素原封不動新增進堆積
    maxHeap = new List<int>(nums);
    // 堆積化除葉節點以外的其他所有節點
    var size = Parent(this.Size() - 1);
    for (int i = size; i >= 0; i--) {
        SiftDown(i);
    }
}
my_heap.go
/* 建構子，根據切片建堆積 */
func newMaxHeap(nums []any) *maxHeap {
    // 將串列元素原封不動新增進堆積
    h := &maxHeap{data: nums}
    for i := h.parent(len(h.data) - 1); i >= 0; i-- {
        // 堆積化除葉節點以外的其他所有節點
        h.siftDown(i)
    }
    return h
}
my_heap.swift
/* 建構子，根據輸入串列建堆積 */
init(nums: [Int]) {
    // 將串列元素原封不動新增進堆積
    maxHeap = nums
    // 堆積化除葉節點以外的其他所有節點
    for i in (0 ... parent(i: size() - 1)).reversed() {
        siftDown(i: i)
    }
}
my_heap.js
/* 建構子，建立空堆積或根據輸入串列建堆積 */
constructor(nums) {
    // 將串列元素原封不動新增進堆積
    this.#maxHeap = nums === undefined ? [] : [...nums];
    // 堆積化除葉節點以外的其他所有節點
    for (let i = this.#parent(this.size() - 1); i >= 0; i--) {
        this.#siftDown(i);
    }
}
my_heap.ts
/* 建構子，建立空堆積或根據輸入串列建堆積 */
constructor(nums?: number[]) {
    // 將串列元素原封不動新增進堆積
    this.maxHeap = nums === undefined ? [] : [...nums];
    // 堆積化除葉節點以外的其他所有節點
    for (let i = this.parent(this.size() - 1); i >= 0; i--) {
        this.siftDown(i);
    }
}
my_heap.dart
/* 建構子，根據輸入串列建堆積 */
MaxHeap(List<int> nums) {
  // 將串列元素原封不動新增進堆積
  _maxHeap = nums;
  // 堆積化除葉節點以外的其他所有節點
  for (int i = _parent(size() - 1); i >= 0; i--) {
    siftDown(i);
  }
}
my_heap.rs
/* 建構子，根據輸入串列建堆積 */
fn new(nums: Vec<i32>) -> Self {
    // 將串列元素原封不動新增進堆積
    let mut heap = MaxHeap { max_heap: nums };
    // 堆積化除葉節點以外的其他所有節點
    for i in (0..=Self::parent(heap.size() - 1)).rev() {
        heap.sift_down(i);
    }
    heap
}
my_heap.c
/* 建構子，根據切片建堆積 */
MaxHeap *newMaxHeap(int nums[], int size) {
    // 所有元素入堆積
    MaxHeap *maxHeap = (MaxHeap *)malloc(sizeof(MaxHeap));
    maxHeap->size = size;
    memcpy(maxHeap->data, nums, size * sizeof(int));
    for (int i = parent(maxHeap, size - 1); i >= 0; i--) {
        // 堆積化除葉節點以外的其他所有節點
        siftDown(maxHeap, i);
    }
    return maxHeap;
}
my_heap.kt
/* 大頂堆積 */
class MaxHeap(nums: List<Int>?) {
    // 使用串列而非陣列，這樣無須考慮擴容問題
    // 將串列元素原封不動新增進堆積
    private val maxHeap = ArrayList(nums!!)

    /* 建構子，根據輸入串列建堆積 */
    init {
        // 堆積化除葉節點以外的其他所有節點
        for (i in parent(size() - 1) downTo 0) {
            siftDown(i)
        }
    }

    /* 獲取左子節點的索引 */
    private fun left(i: Int): Int {
        return 2 * i + 1
    }

    /* 獲取右子節點的索引 */
    private fun right(i: Int): Int {
        return 2 * i + 2
    }

    /* 獲取父節點的索引 */
    private fun parent(i: Int): Int {
        return (i - 1) / 2 // 向下整除
    }

    /* 交換元素 */
    private fun swap(i: Int, j: Int) {
        maxHeap[i] = maxHeap[j].also { maxHeap[j] = maxHeap[i] }
    }

    /* 獲取堆積大小 */
    fun size(): Int {
        return maxHeap.size
    }

    /* 判斷堆積是否為空 */
    fun isEmpty(): Boolean {
        /* 判斷堆積是否為空 */
        return size() == 0
    }

    /* 訪問堆積頂元素 */
    fun peek(): Int {
        return maxHeap[0]
    }

    /* 元素入堆積 */
    fun push(value: Int) {
        // 新增節點
        maxHeap.add(value)
        // 從底至頂堆積化
        siftUp(size() - 1)
    }

    /* 從節點 i 開始，從底至頂堆積化 */
    private fun siftUp(it: Int) {
        // Kotlin的函式參數不可變，因此建立臨時變數
        var i = it
        while (true) {
            // 獲取節點 i 的父節點
            val p = parent(i)
            // 當“越過根節點”或“節點無須修復”時，結束堆積化
            if (p < 0 || maxHeap[i] <= maxHeap[p]) break
            // 交換兩節點
            swap(i, p)
            // 迴圈向上堆積化
            i = p
        }
    }

    /* 元素出堆積 */
    fun pop(): Int {
        // 判空處理
        if (isEmpty()) throw IndexOutOfBoundsException()
        // 交換根節點與最右葉節點（交換首元素與尾元素）
        swap(0, size() - 1)
        // 刪除節點
        val value = maxHeap.removeAt(size() - 1)
        // 從頂至底堆積化
        siftDown(0)
        // 返回堆積頂元素
        return value
    }

    /* 從節點 i 開始，從頂至底堆積化 */
    private fun siftDown(it: Int) {
        // Kotlin的函式參數不可變，因此建立臨時變數
        var i = it
        while (true) {
            // 判斷節點 i, l, r 中值最大的節點，記為 ma
            val l = left(i)
            val r = right(i)
            var ma = i
            if (l < size() && maxHeap[l] > maxHeap[ma]) ma = l
            if (r < size() && maxHeap[r] > maxHeap[ma]) ma = r
            // 若節點 i 最大或索引 l, r 越界，則無須繼續堆積化，跳出
            if (ma == i) break
            // 交換兩節點
            swap(i, ma)
            // 迴圈向下堆積化
            i = ma
        }
    }

    /* 列印堆積（二元樹） */
    fun print() {
        val queue = PriorityQueue { a: Int, b: Int -> b - a }
        queue.addAll(maxHeap)
        printHeap(queue)
    }
}
my_heap.rb
[class]{MaxHeap}-[func]{__init__}
my_heap.zig
// 建構子，根據輸入串列建堆積
fn init(self: *Self, allocator: std.mem.Allocator, nums: []const T) !void {
    if (self.max_heap != null) return;
    self.max_heap = std.ArrayList(T).init(allocator);
    // 將串列元素原封不動新增進堆積
    try self.max_heap.?.appendSlice(nums);
    // 堆積化除葉節點以外的其他所有節點
    var i: usize = parent(self.size() - 1) + 1;
    while (i > 0) : (i -= 1) {
        try self.siftDown(i - 1);
    }
}
視覺化執行

8.2.3   複雜度分析

下面，我們來嘗試推算第二種建堆積方法的時間複雜度。

  • 假設完全二元樹的節點數量為 \(n\) ，則葉節點數量為 \((n + 1) / 2\) ，其中 \(/\) 為向下整除。因此需要堆積化的節點數量為 \((n - 1) / 2\) 。
  • 在從頂至底堆積化的過程中，每個節點最多堆積化到葉節點，因此最大迭代次數為二元樹高度 \(\log n\) 。

將上述兩者相乘，可得到建堆積過程的時間複雜度為 \(O(n \log n)\) 。但這個估算結果並不準確，因為我們沒有考慮到二元樹底層節點數量遠多於頂層節點的性質。

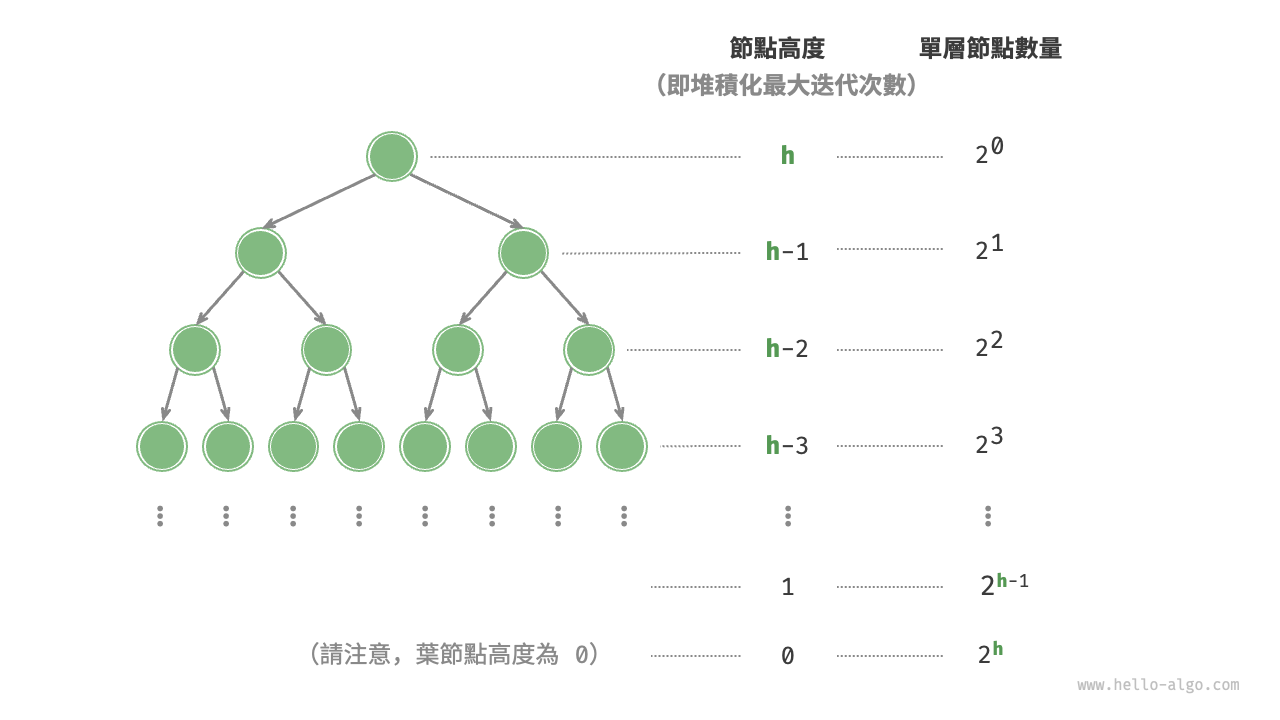
接下來我們來進行更為準確的計算。為了降低計算難度，假設給定一個節點數量為 \(n\) 、高度為 \(h\) 的“完美二元樹”，該假設不會影響計算結果的正確性。

完美二元樹的各層節點數量

圖 8-5   完美二元樹的各層節點數量

如圖 8-5 所示，節點“從頂至底堆積化”的最大迭代次數等於該節點到葉節點的距離，而該距離正是“節點高度”。因此，我們可以對各層的“節點數量 \(\times\) 節點高度”求和，得到所有節點的堆積化迭代次數的總和。

\[ T(h) = 2^0h + 2^1(h-1) + 2^2(h-2) + \dots + 2^{(h-1)}\times1 \]

化簡上式需要藉助中學的數列知識，先將 \(T(h)\) 乘以 \(2\) ，得到：

\[ \begin{aligned} T(h) & = 2^0h + 2^1(h-1) + 2^2(h-2) + \dots + 2^{h-1}\times1 \newline 2 T(h) & = 2^1h + 2^2(h-1) + 2^3(h-2) + \dots + 2^{h}\times1 \newline \end{aligned} \]

使用錯位相減法，用下式 \(2 T(h)\) 減去上式 \(T(h)\) ，可得：

\[ 2T(h) - T(h) = T(h) = -2^0h + 2^1 + 2^2 + \dots + 2^{h-1} + 2^h \]

觀察上式，發現 \(T(h)\) 是一個等比數列，可直接使用求和公式，得到時間複雜度為：

\[ \begin{aligned} T(h) & = 2 \frac{1 - 2^h}{1 - 2} - h \newline & = 2^{h+1} - h - 2 \newline & = O(2^h) \end{aligned} \]

進一步，高度為 \(h\) 的完美二元樹的節點數量為 \(n = 2^{h+1} - 1\) ，易得複雜度為 \(O(2^h) = O(n)\) 。以上推算表明，輸入串列並建堆積的時間複雜度為 \(O(n)\) ，非常高效。