跳轉至

10.1   二分搜尋

二分搜尋（binary search）是一種基於分治策略的高效搜尋演算法。它利用資料的有序性，每輪縮小一半搜尋範圍，直至找到目標元素或搜尋區間為空為止。

Question

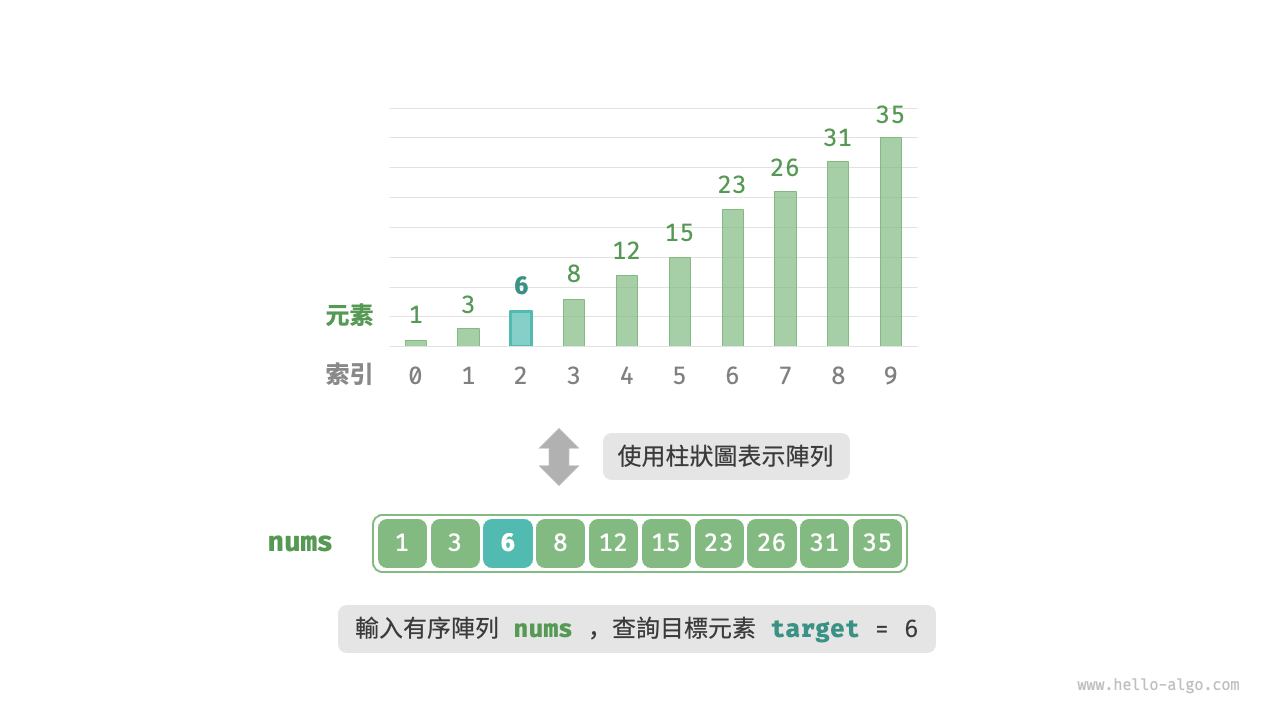
給定一個長度為 \(n\) 的陣列 nums ，元素按從小到大的順序排列且不重複。請查詢並返回元素 target 在該陣列中的索引。若陣列不包含該元素，則返回 \(-1\) 。示例如圖 10-1 所示。

二分搜尋示例資料

圖 10-1   二分搜尋示例資料

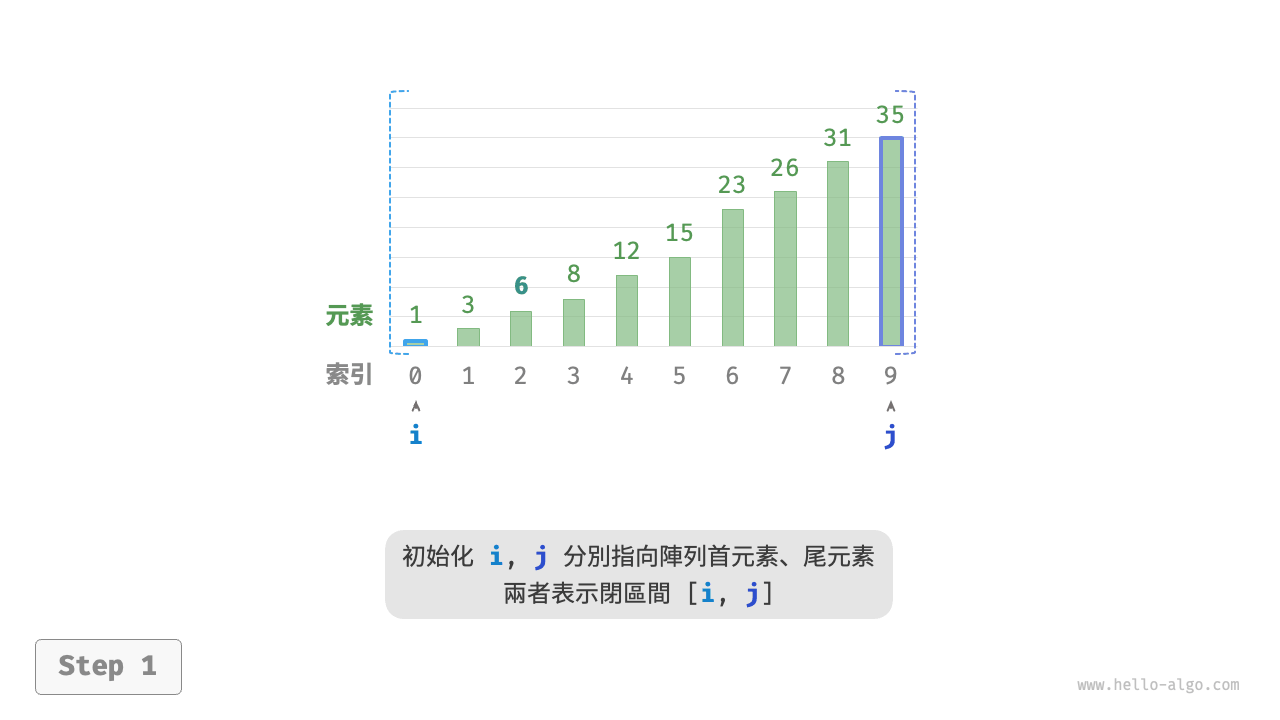
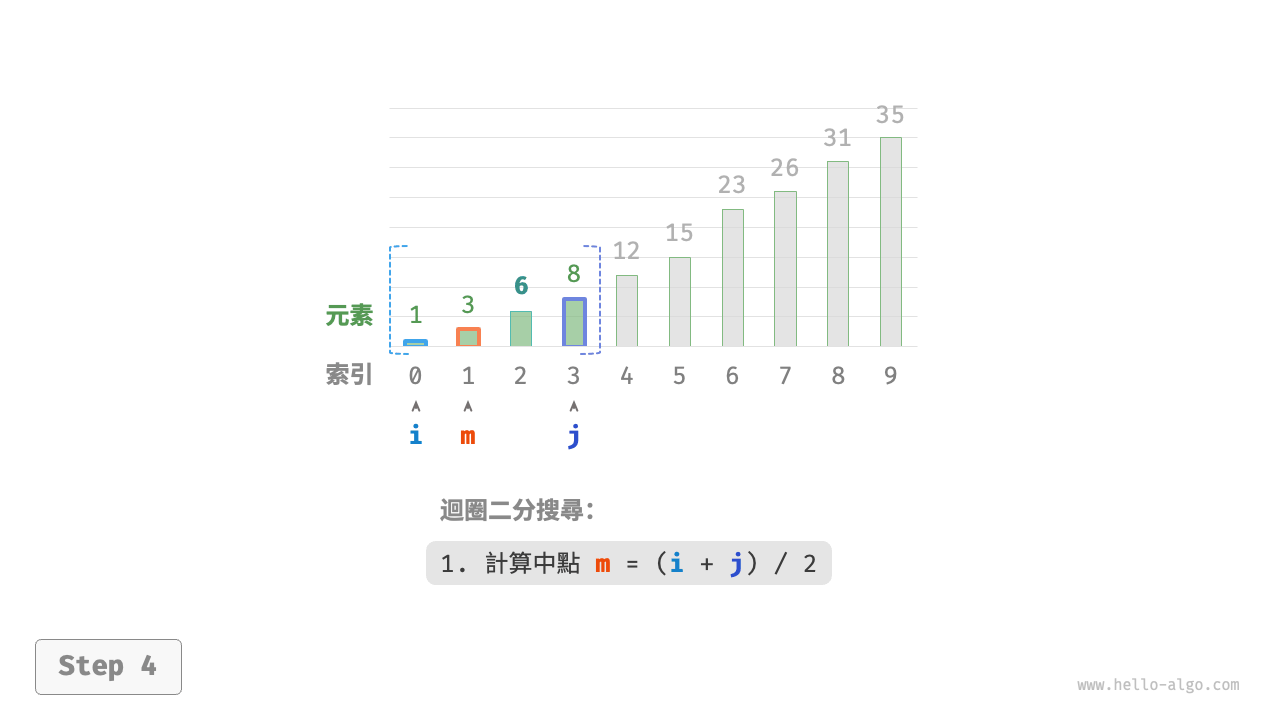
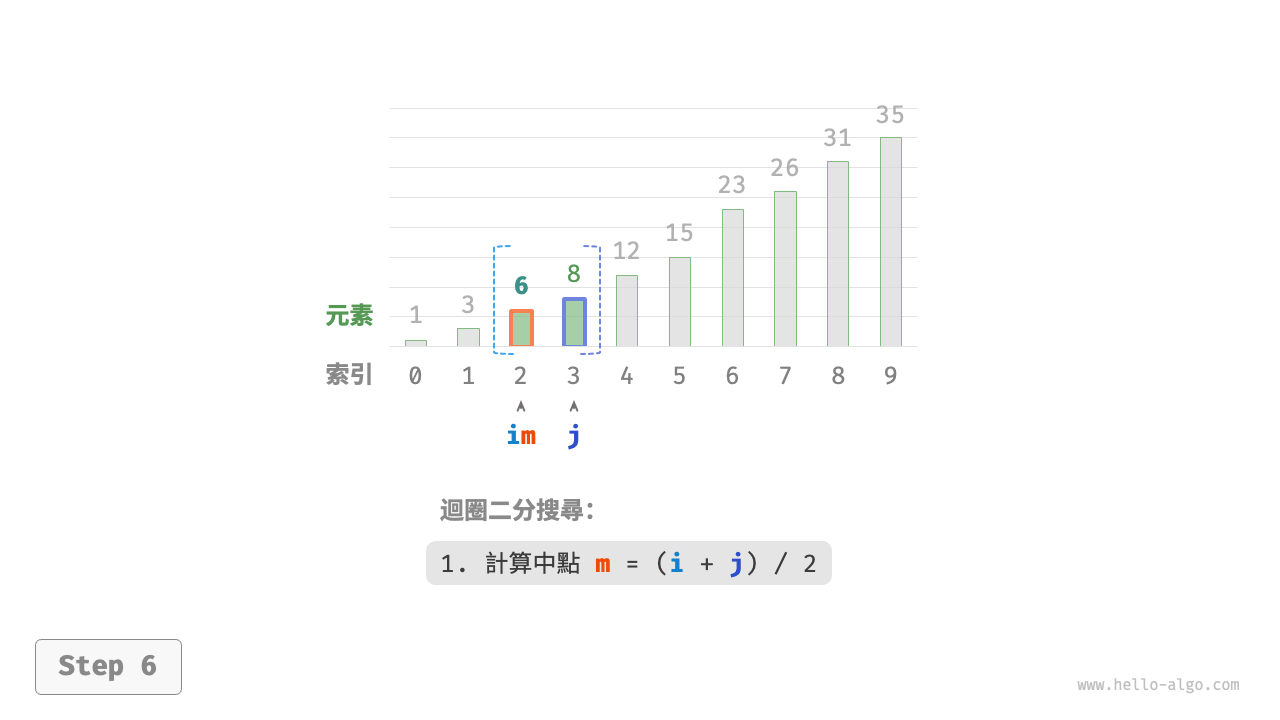
如圖 10-2 所示，我們先初始化指標 \(i = 0\) 和 \(j = n - 1\) ，分別指向陣列首元素和尾元素，代表搜尋區間 \([0, n - 1]\) 。請注意，中括號表示閉區間，其包含邊界值本身。

接下來，迴圈執行以下兩步。

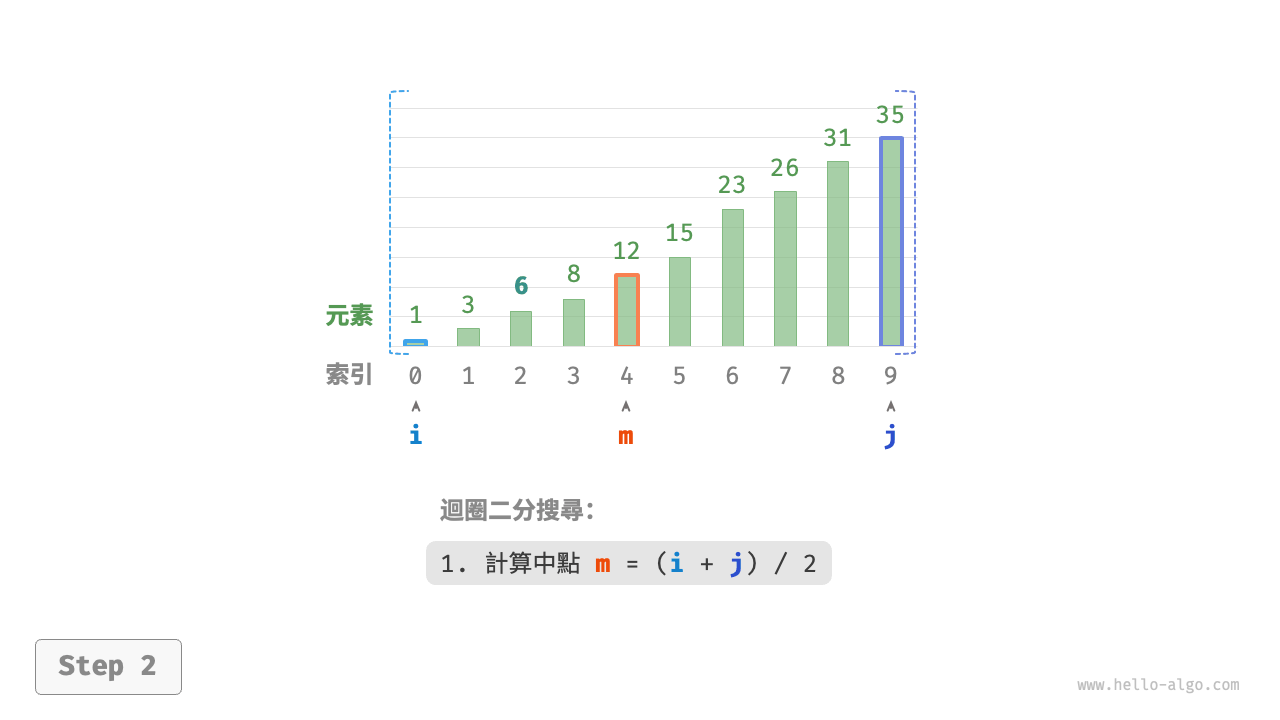
  1. 計算中點索引 \(m = \lfloor {(i + j) / 2} \rfloor\) ，其中 \(\lfloor \: \rfloor\) 表示向下取整操作。
  2. 判斷 nums[m] 和 target 的大小關係，分為以下三種情況。
    1. 當 nums[m] < target 時，說明 target 在區間 \([m + 1, j]\) 中，因此執行 \(i = m + 1\) 。
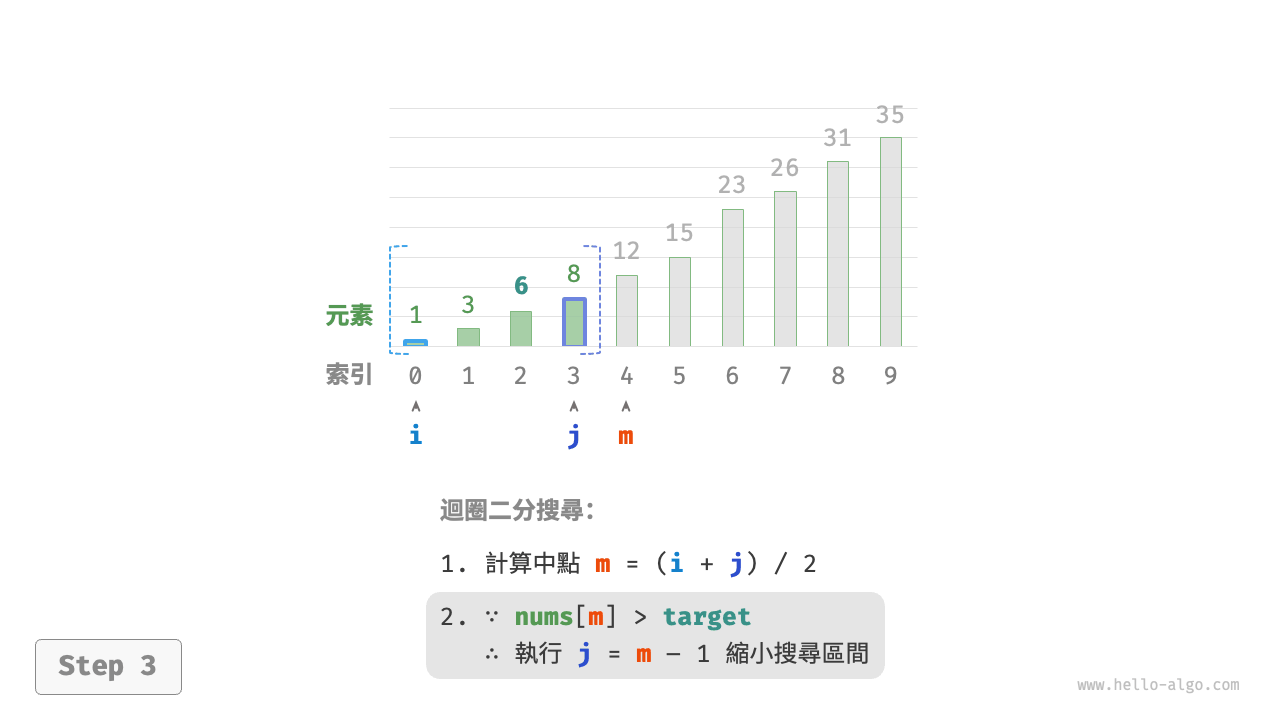
    2. 當 nums[m] > target 時，說明 target 在區間 \([i, m - 1]\) 中，因此執行 \(j = m - 1\) 。
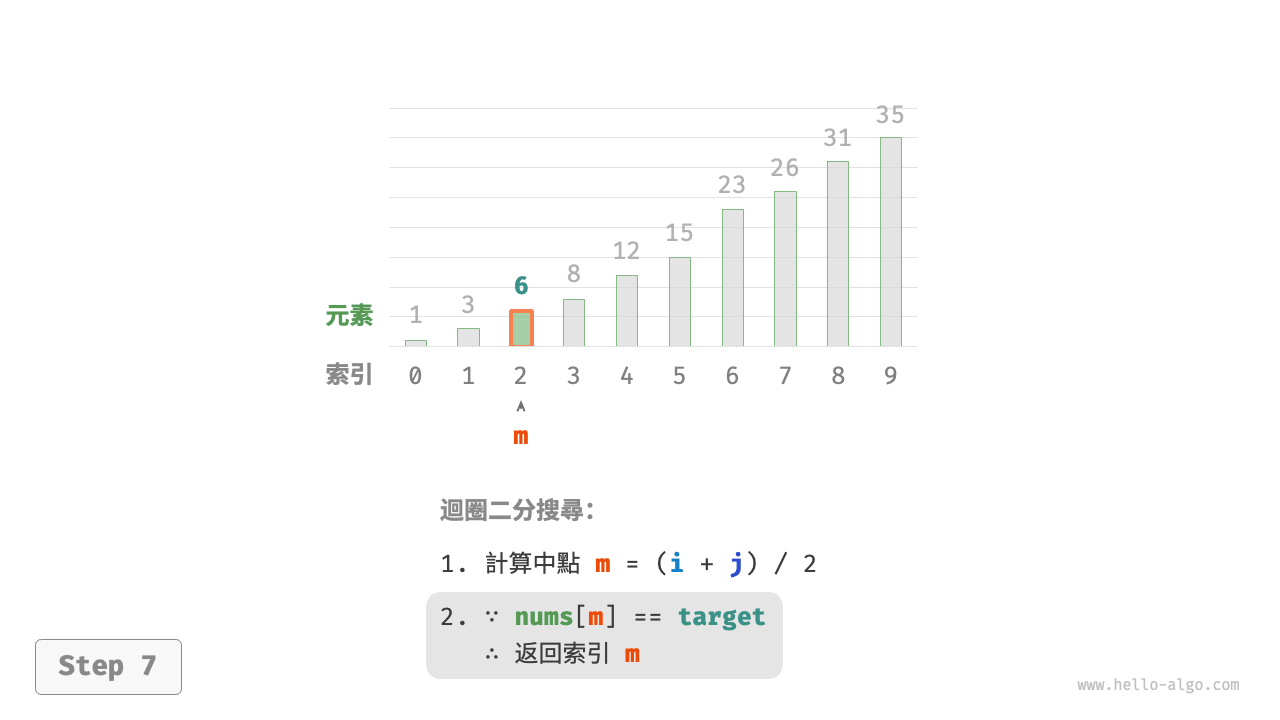
    3. 當 nums[m] = target 時，說明找到 target ，因此返回索引 \(m\) 。

若陣列不包含目標元素，搜尋區間最終會縮小為空。此時返回 \(-1\) 。

二分搜尋流程

binary_search_step2

binary_search_step3

binary_search_step4

binary_search_step5

binary_search_step6

binary_search_step7

圖 10-2   二分搜尋流程

值得注意的是，由於 \(i\) 和 \(j\) 都是 int 型別，因此 \(i + j\) 可能會超出 int 型別的取值範圍。為了避免大數越界，我們通常採用公式 \(m = \lfloor {i + (j - i) / 2} \rfloor\) 來計算中點。

程式碼如下所示：

binary_search.py
def binary_search(nums: list[int], target: int) -> int:
    """二分搜尋（雙閉區間）"""
    # 初始化雙閉區間 [0, n-1] ，即 i, j 分別指向陣列首元素、尾元素
    i, j = 0, len(nums) - 1
    # 迴圈，當搜尋區間為空時跳出（當 i > j 時為空）
    while i <= j:
        # 理論上 Python 的數字可以無限大（取決於記憶體大小），無須考慮大數越界問題
        m = (i + j) // 2  # 計算中點索引 m
        if nums[m] < target:
            i = m + 1  # 此情況說明 target 在區間 [m+1, j] 中
        elif nums[m] > target:
            j = m - 1  # 此情況說明 target 在區間 [i, m-1] 中
        else:
            return m  # 找到目標元素，返回其索引
    return -1  # 未找到目標元素，返回 -1
binary_search.cpp
/* 二分搜尋（雙閉區間） */
int binarySearch(vector<int> &nums, int target) {
    // 初始化雙閉區間 [0, n-1] ，即 i, j 分別指向陣列首元素、尾元素
    int i = 0, j = nums.size() - 1;
    // 迴圈，當搜尋區間為空時跳出（當 i > j 時為空）
    while (i <= j) {
        int m = i + (j - i) / 2; // 計算中點索引 m
        if (nums[m] < target)    // 此情況說明 target 在區間 [m+1, j] 中
            i = m + 1;
        else if (nums[m] > target) // 此情況說明 target 在區間 [i, m-1] 中
            j = m - 1;
        else // 找到目標元素，返回其索引
            return m;
    }
    // 未找到目標元素，返回 -1
    return -1;
}
binary_search.java
/* 二分搜尋（雙閉區間） */
int binarySearch(int[] nums, int target) {
    // 初始化雙閉區間 [0, n-1] ，即 i, j 分別指向陣列首元素、尾元素
    int i = 0, j = nums.length - 1;
    // 迴圈，當搜尋區間為空時跳出（當 i > j 時為空）
    while (i <= j) {
        int m = i + (j - i) / 2; // 計算中點索引 m
        if (nums[m] < target) // 此情況說明 target 在區間 [m+1, j] 中
            i = m + 1;
        else if (nums[m] > target) // 此情況說明 target 在區間 [i, m-1] 中
            j = m - 1;
        else // 找到目標元素，返回其索引
            return m;
    }
    // 未找到目標元素，返回 -1
    return -1;
}
binary_search.cs
/* 二分搜尋（雙閉區間） */
int BinarySearch(int[] nums, int target) {
    // 初始化雙閉區間 [0, n-1] ，即 i, j 分別指向陣列首元素、尾元素
    int i = 0, j = nums.Length - 1;
    // 迴圈，當搜尋區間為空時跳出（當 i > j 時為空）
    while (i <= j) {
        int m = i + (j - i) / 2;   // 計算中點索引 m
        if (nums[m] < target)      // 此情況說明 target 在區間 [m+1, j] 中
            i = m + 1;
        else if (nums[m] > target) // 此情況說明 target 在區間 [i, m-1] 中
            j = m - 1;
        else                       // 找到目標元素，返回其索引
            return m;
    }
    // 未找到目標元素，返回 -1
    return -1;
}
binary_search.go
/* 二分搜尋（雙閉區間） */
func binarySearch(nums []int, target int) int {
    // 初始化雙閉區間 [0, n-1] ，即 i, j 分別指向陣列首元素、尾元素
    i, j := 0, len(nums)-1
    // 迴圈，當搜尋區間為空時跳出（當 i > j 時為空）
    for i <= j {
        m := i + (j-i)/2      // 計算中點索引 m
        if nums[m] < target { // 此情況說明 target 在區間 [m+1, j] 中
            i = m + 1
        } else if nums[m] > target { // 此情況說明 target 在區間 [i, m-1] 中
            j = m - 1
        } else { // 找到目標元素，返回其索引
            return m
        }
    }
    // 未找到目標元素，返回 -1
    return -1
}
binary_search.swift
/* 二分搜尋（雙閉區間） */
func binarySearch(nums: [Int], target: Int) -> Int {
    // 初始化雙閉區間 [0, n-1] ，即 i, j 分別指向陣列首元素、尾元素
    var i = nums.startIndex
    var j = nums.endIndex - 1
    // 迴圈，當搜尋區間為空時跳出（當 i > j 時為空）
    while i <= j {
        let m = i + (j - i) / 2 // 計算中點索引 m
        if nums[m] < target { // 此情況說明 target 在區間 [m+1, j] 中
            i = m + 1
        } else if nums[m] > target { // 此情況說明 target 在區間 [i, m-1] 中
            j = m - 1
        } else { // 找到目標元素，返回其索引
            return m
        }
    }
    // 未找到目標元素，返回 -1
    return -1
}
binary_search.js
/* 二分搜尋（雙閉區間） */
function binarySearch(nums, target) {
    // 初始化雙閉區間 [0, n-1] ，即 i, j 分別指向陣列首元素、尾元素
    let i = 0,
        j = nums.length - 1;
    // 迴圈，當搜尋區間為空時跳出（當 i > j 時為空）
    while (i <= j) {
        // 計算中點索引 m ，使用 parseInt() 向下取整
        const m = parseInt(i + (j - i) / 2);
        if (nums[m] < target)
            // 此情況說明 target 在區間 [m+1, j] 中
            i = m + 1;
        else if (nums[m] > target)
            // 此情況說明 target 在區間 [i, m-1] 中
            j = m - 1;
        else return m; // 找到目標元素，返回其索引
    }
    // 未找到目標元素，返回 -1
    return -1;
}
binary_search.ts
/* 二分搜尋（雙閉區間） */
function binarySearch(nums: number[], target: number): number {
    // 初始化雙閉區間 [0, n-1] ，即 i, j 分別指向陣列首元素、尾元素
    let i = 0,
        j = nums.length - 1;
    // 迴圈，當搜尋區間為空時跳出（當 i > j 時為空）
    while (i <= j) {
        // 計算中點索引 m
        const m = Math.floor(i + (j - i) / 2);
        if (nums[m] < target) {
            // 此情況說明 target 在區間 [m+1, j] 中
            i = m + 1;
        } else if (nums[m] > target) {
            // 此情況說明 target 在區間 [i, m-1] 中
            j = m - 1;
        } else {
            // 找到目標元素，返回其索引
            return m;
        }
    }
    return -1; // 未找到目標元素，返回 -1
}
binary_search.dart
/* 二分搜尋（雙閉區間） */
int binarySearch(List<int> nums, int target) {
  // 初始化雙閉區間 [0, n-1] ，即 i, j 分別指向陣列首元素、尾元素
  int i = 0, j = nums.length - 1;
  // 迴圈，當搜尋區間為空時跳出（當 i > j 時為空）
  while (i <= j) {
    int m = i + (j - i) ~/ 2; // 計算中點索引 m
    if (nums[m] < target) {
      // 此情況說明 target 在區間 [m+1, j] 中
      i = m + 1;
    } else if (nums[m] > target) {
      // 此情況說明 target 在區間 [i, m-1] 中
      j = m - 1;
    } else {
      // 找到目標元素，返回其索引
      return m;
    }
  }
  // 未找到目標元素，返回 -1
  return -1;
}
binary_search.rs
/* 二分搜尋（雙閉區間） */
fn binary_search(nums: &[i32], target: i32) -> i32 {
    // 初始化雙閉區間 [0, n-1] ，即 i, j 分別指向陣列首元素、尾元素
    let mut i = 0;
    let mut j = nums.len() as i32 - 1;
    // 迴圈，當搜尋區間為空時跳出（當 i > j 時為空）
    while i <= j {
        let m = i + (j - i) / 2; // 計算中點索引 m
        if nums[m as usize] < target {
            // 此情況說明 target 在區間 [m+1, j] 中
            i = m + 1;
        } else if nums[m as usize] > target {
            // 此情況說明 target 在區間 [i, m-1] 中
            j = m - 1;
        } else {
            // 找到目標元素，返回其索引
            return m;
        }
    }
    // 未找到目標元素，返回 -1
    return -1;
}
binary_search.c
/* 二分搜尋（雙閉區間） */
int binarySearch(int *nums, int len, int target) {
    // 初始化雙閉區間 [0, n-1] ，即 i, j 分別指向陣列首元素、尾元素
    int i = 0, j = len - 1;
    // 迴圈，當搜尋區間為空時跳出（當 i > j 時為空）
    while (i <= j) {
        int m = i + (j - i) / 2; // 計算中點索引 m
        if (nums[m] < target)    // 此情況說明 target 在區間 [m+1, j] 中
            i = m + 1;
        else if (nums[m] > target) // 此情況說明 target 在區間 [i, m-1] 中
            j = m - 1;
        else // 找到目標元素，返回其索引
            return m;
    }
    // 未找到目標元素，返回 -1
    return -1;
}
binary_search.kt
/* 二分搜尋（雙閉區間） */
fun binarySearch(nums: IntArray, target: Int): Int {
    // 初始化雙閉區間 [0, n-1] ，即 i, j 分別指向陣列首元素、尾元素
    var i = 0
    var j = nums.size - 1
    // 迴圈，當搜尋區間為空時跳出（當 i > j 時為空）
    while (i <= j) {
        val m = i + (j - i) / 2 // 計算中點索引 m
        if (nums[m] < target) // 此情況說明 target 在區間 [m+1, j] 中
            i = m + 1
        else if (nums[m] > target) // 此情況說明 target 在區間 [i, m-1] 中
            j = m - 1
        else  // 找到目標元素，返回其索引
            return m
    }
    // 未找到目標元素，返回 -1
    return -1
}
binary_search.rb
[class]{}-[func]{binary_search}
binary_search.zig
// 二分搜尋（雙閉區間）
fn binarySearch(comptime T: type, nums: std.ArrayList(T), target: T) T {
    // 初始化雙閉區間 [0, n-1] ，即 i, j 分別指向陣列首元素、尾元素
    var i: usize = 0;
    var j: usize = nums.items.len - 1;
    // 迴圈，當搜尋區間為空時跳出（當 i > j 時為空）
    while (i <= j) {
        var m = i + (j - i) / 2;                // 計算中點索引 m
        if (nums.items[m] < target) {           // 此情況說明 target 在區間 [m+1, j] 中
            i = m + 1;
        } else if (nums.items[m] > target) {    // 此情況說明 target 在區間 [i, m-1] 中
            j = m - 1;
        } else {                                // 找到目標元素，返回其索引
            return @intCast(m);
        }
    }
    // 未找到目標元素，返回 -1
    return -1;
}
視覺化執行

時間複雜度為 \(O(\log n)\) ：在二分迴圈中，區間每輪縮小一半，因此迴圈次數為 \(\log_2 n\) 。

空間複雜度為 \(O(1)\) ：指標 \(i\) 和 \(j\) 使用常數大小空間。

10.1.1   區間表示方法

除了上述雙閉區間外，常見的區間表示還有“左閉右開”區間，定義為 \([0, n)\) ，即左邊界包含自身，右邊界不包含自身。在該表示下，區間 \([i, j)\) 在 \(i = j\) 時為空。

我們可以基於該表示實現具有相同功能的二分搜尋演算法：

binary_search.py
def binary_search_lcro(nums: list[int], target: int) -> int:
    """二分搜尋（左閉右開區間）"""
    # 初始化左閉右開區間 [0, n) ，即 i, j 分別指向陣列首元素、尾元素+1
    i, j = 0, len(nums)
    # 迴圈，當搜尋區間為空時跳出（當 i = j 時為空）
    while i < j:
        m = (i + j) // 2  # 計算中點索引 m
        if nums[m] < target:
            i = m + 1  # 此情況說明 target 在區間 [m+1, j) 中
        elif nums[m] > target:
            j = m  # 此情況說明 target 在區間 [i, m) 中
        else:
            return m  # 找到目標元素，返回其索引
    return -1  # 未找到目標元素，返回 -1
binary_search.cpp
/* 二分搜尋（左閉右開區間） */
int binarySearchLCRO(vector<int> &nums, int target) {
    // 初始化左閉右開區間 [0, n) ，即 i, j 分別指向陣列首元素、尾元素+1
    int i = 0, j = nums.size();
    // 迴圈，當搜尋區間為空時跳出（當 i = j 時為空）
    while (i < j) {
        int m = i + (j - i) / 2; // 計算中點索引 m
        if (nums[m] < target)    // 此情況說明 target 在區間 [m+1, j) 中
            i = m + 1;
        else if (nums[m] > target) // 此情況說明 target 在區間 [i, m) 中
            j = m;
        else // 找到目標元素，返回其索引
            return m;
    }
    // 未找到目標元素，返回 -1
    return -1;
}
binary_search.java
/* 二分搜尋（左閉右開區間） */
int binarySearchLCRO(int[] nums, int target) {
    // 初始化左閉右開區間 [0, n) ，即 i, j 分別指向陣列首元素、尾元素+1
    int i = 0, j = nums.length;
    // 迴圈，當搜尋區間為空時跳出（當 i = j 時為空）
    while (i < j) {
        int m = i + (j - i) / 2; // 計算中點索引 m
        if (nums[m] < target) // 此情況說明 target 在區間 [m+1, j) 中
            i = m + 1;
        else if (nums[m] > target) // 此情況說明 target 在區間 [i, m) 中
            j = m;
        else // 找到目標元素，返回其索引
            return m;
    }
    // 未找到目標元素，返回 -1
    return -1;
}
binary_search.cs
/* 二分搜尋（左閉右開區間） */
int BinarySearchLCRO(int[] nums, int target) {
    // 初始化左閉右開區間 [0, n) ，即 i, j 分別指向陣列首元素、尾元素+1
    int i = 0, j = nums.Length;
    // 迴圈，當搜尋區間為空時跳出（當 i = j 時為空）
    while (i < j) {
        int m = i + (j - i) / 2;   // 計算中點索引 m
        if (nums[m] < target)      // 此情況說明 target 在區間 [m+1, j) 中
            i = m + 1;
        else if (nums[m] > target) // 此情況說明 target 在區間 [i, m) 中
            j = m;
        else                       // 找到目標元素，返回其索引
            return m;
    }
    // 未找到目標元素，返回 -1
    return -1;
}
binary_search.go
/* 二分搜尋（左閉右開區間） */
func binarySearchLCRO(nums []int, target int) int {
    // 初始化左閉右開區間 [0, n) ，即 i, j 分別指向陣列首元素、尾元素+1
    i, j := 0, len(nums)
    // 迴圈，當搜尋區間為空時跳出（當 i = j 時為空）
    for i < j {
        m := i + (j-i)/2      // 計算中點索引 m
        if nums[m] < target { // 此情況說明 target 在區間 [m+1, j) 中
            i = m + 1
        } else if nums[m] > target { // 此情況說明 target 在區間 [i, m) 中
            j = m
        } else { // 找到目標元素，返回其索引
            return m
        }
    }
    // 未找到目標元素，返回 -1
    return -1
}
binary_search.swift
/* 二分搜尋（左閉右開區間） */
func binarySearchLCRO(nums: [Int], target: Int) -> Int {
    // 初始化左閉右開區間 [0, n) ，即 i, j 分別指向陣列首元素、尾元素+1
    var i = nums.startIndex
    var j = nums.endIndex
    // 迴圈，當搜尋區間為空時跳出（當 i = j 時為空）
    while i < j {
        let m = i + (j - i) / 2 // 計算中點索引 m
        if nums[m] < target { // 此情況說明 target 在區間 [m+1, j) 中
            i = m + 1
        } else if nums[m] > target { // 此情況說明 target 在區間 [i, m) 中
            j = m
        } else { // 找到目標元素，返回其索引
            return m
        }
    }
    // 未找到目標元素，返回 -1
    return -1
}
binary_search.js
/* 二分搜尋（左閉右開區間） */
function binarySearchLCRO(nums, target) {
    // 初始化左閉右開區間 [0, n) ，即 i, j 分別指向陣列首元素、尾元素+1
    let i = 0,
        j = nums.length;
    // 迴圈，當搜尋區間為空時跳出（當 i = j 時為空）
    while (i < j) {
        // 計算中點索引 m ，使用 parseInt() 向下取整
        const m = parseInt(i + (j - i) / 2);
        if (nums[m] < target)
            // 此情況說明 target 在區間 [m+1, j) 中
            i = m + 1;
        else if (nums[m] > target)
            // 此情況說明 target 在區間 [i, m) 中
            j = m;
        // 找到目標元素，返回其索引
        else return m;
    }
    // 未找到目標元素，返回 -1
    return -1;
}
binary_search.ts
/* 二分搜尋（左閉右開區間） */
function binarySearchLCRO(nums: number[], target: number): number {
    // 初始化左閉右開區間 [0, n) ，即 i, j 分別指向陣列首元素、尾元素+1
    let i = 0,
        j = nums.length;
    // 迴圈，當搜尋區間為空時跳出（當 i = j 時為空）
    while (i < j) {
        // 計算中點索引 m
        const m = Math.floor(i + (j - i) / 2);
        if (nums[m] < target) {
            // 此情況說明 target 在區間 [m+1, j) 中
            i = m + 1;
        } else if (nums[m] > target) {
            // 此情況說明 target 在區間 [i, m) 中
            j = m;
        } else {
            // 找到目標元素，返回其索引
            return m;
        }
    }
    return -1; // 未找到目標元素，返回 -1
}
binary_search.dart
/* 二分搜尋（左閉右開區間） */
int binarySearchLCRO(List<int> nums, int target) {
  // 初始化左閉右開區間 [0, n) ，即 i, j 分別指向陣列首元素、尾元素+1
  int i = 0, j = nums.length;
  // 迴圈，當搜尋區間為空時跳出（當 i = j 時為空）
  while (i < j) {
    int m = i + (j - i) ~/ 2; // 計算中點索引 m
    if (nums[m] < target) {
      // 此情況說明 target 在區間 [m+1, j) 中
      i = m + 1;
    } else if (nums[m] > target) {
      // 此情況說明 target 在區間 [i, m) 中
      j = m;
    } else {
      // 找到目標元素，返回其索引
      return m;
    }
  }
  // 未找到目標元素，返回 -1
  return -1;
}
binary_search.rs
/* 二分搜尋（左閉右開區間） */
fn binary_search_lcro(nums: &[i32], target: i32) -> i32 {
    // 初始化左閉右開區間 [0, n) ，即 i, j 分別指向陣列首元素、尾元素+1
    let mut i = 0;
    let mut j = nums.len() as i32;
    // 迴圈，當搜尋區間為空時跳出（當 i = j 時為空）
    while i < j {
        let m = i + (j - i) / 2; // 計算中點索引 m
        if nums[m as usize] < target {
            // 此情況說明 target 在區間 [m+1, j) 中
            i = m + 1;
        } else if nums[m as usize] > target {
            // 此情況說明 target 在區間 [i, m) 中
            j = m;
        } else {
            // 找到目標元素，返回其索引
            return m;
        }
    }
    // 未找到目標元素，返回 -1
    return -1;
}
binary_search.c
/* 二分搜尋（左閉右開區間） */
int binarySearchLCRO(int *nums, int len, int target) {
    // 初始化左閉右開區間 [0, n) ，即 i, j 分別指向陣列首元素、尾元素+1
    int i = 0, j = len;
    // 迴圈，當搜尋區間為空時跳出（當 i = j 時為空）
    while (i < j) {
        int m = i + (j - i) / 2; // 計算中點索引 m
        if (nums[m] < target)    // 此情況說明 target 在區間 [m+1, j) 中
            i = m + 1;
        else if (nums[m] > target) // 此情況說明 target 在區間 [i, m) 中
            j = m;
        else // 找到目標元素，返回其索引
            return m;
    }
    // 未找到目標元素，返回 -1
    return -1;
}
binary_search.kt
/* 二分搜尋（左閉右開區間） */
fun binarySearchLCRO(nums: IntArray, target: Int): Int {
    // 初始化左閉右開區間 [0, n) ，即 i, j 分別指向陣列首元素、尾元素+1
    var i = 0
    var j = nums.size
    // 迴圈，當搜尋區間為空時跳出（當 i = j 時為空）
    while (i < j) {
        val m = i + (j - i) / 2 // 計算中點索引 m
        if (nums[m] < target) // 此情況說明 target 在區間 [m+1, j) 中
            i = m + 1
        else if (nums[m] > target) // 此情況說明 target 在區間 [i, m) 中
            j = m
        else  // 找到目標元素，返回其索引
            return m
    }
    // 未找到目標元素，返回 -1
    return -1
}
binary_search.rb
[class]{}-[func]{binary_search_lcro}
binary_search.zig
// 二分搜尋（左閉右開區間）
fn binarySearchLCRO(comptime T: type, nums: std.ArrayList(T), target: T) T {
    // 初始化左閉右開區間 [0, n) ，即 i, j 分別指向陣列首元素、尾元素+1
    var i: usize = 0;
    var j: usize = nums.items.len;
    // 迴圈，當搜尋區間為空時跳出（當 i = j 時為空）
    while (i <= j) {
        var m = i + (j - i) / 2;                // 計算中點索引 m
        if (nums.items[m] < target) {           // 此情況說明 target 在區間 [m+1, j) 中
            i = m + 1;
        } else if (nums.items[m] > target) {    // 此情況說明 target 在區間 [i, m) 中
            j = m;
        } else {                                // 找到目標元素，返回其索引
            return @intCast(m);
        }
    }
    // 未找到目標元素，返回 -1
    return -1;
}
視覺化執行

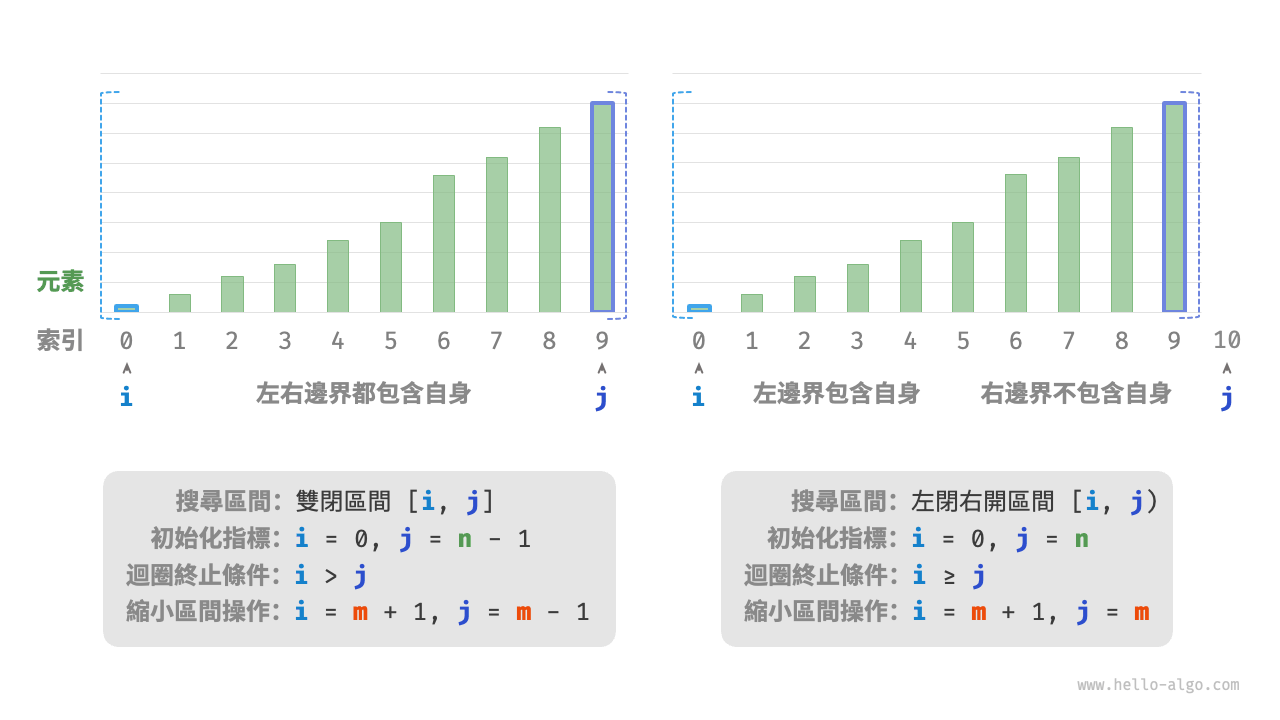
如圖 10-3 所示，在兩種區間表示下，二分搜尋演算法的初始化、迴圈條件和縮小區間操作皆有所不同。

由於“雙閉區間”表示中的左右邊界都被定義為閉區間，因此透過指標 \(i\) 和指標 \(j\) 縮小區間的操作也是對稱的。這樣更不容易出錯，因此一般建議採用“雙閉區間”的寫法。

兩種區間定義

圖 10-3   兩種區間定義

10.1.2   優點與侷限性

二分搜尋在時間和空間方面都有較好的效能。

  • 二分搜尋的時間效率高。在大資料量下，對數階的時間複雜度具有顯著優勢。例如，當資料大小 \(n = 2^{20}\) 時，線性查詢需要 \(2^{20} = 1048576\) 輪迴圈，而二分搜尋僅需 \(\log_2 2^{20} = 20\) 輪迴圈。
  • 二分搜尋無須額外空間。相較於需要藉助額外空間的搜尋演算法（例如雜湊查詢），二分搜尋更加節省空間。

然而，二分搜尋並非適用於所有情況，主要有以下原因。

  • 二分搜尋僅適用於有序資料。若輸入資料無序，為了使用二分搜尋而專門進行排序，得不償失。因為排序演算法的時間複雜度通常為 \(O(n \log n)\) ，比線性查詢和二分搜尋都更高。對於頻繁插入元素的場景，為保持陣列有序性，需要將元素插入到特定位置，時間複雜度為 \(O(n)\) ，也是非常昂貴的。
  • 二分搜尋僅適用於陣列。二分搜尋需要跳躍式（非連續地）訪問元素，而在鏈結串列中執行跳躍式訪問的效率較低，因此不適合應用在鏈結串列或基於鏈結串列實現的資料結構。
  • 小資料量下，線性查詢效能更佳。線上性查詢中，每輪只需 1 次判斷操作；而在二分搜尋中，需要 1 次加法、1 次除法、1 ~ 3 次判斷操作、1 次加法（減法），共 4 ~ 6 個單元操作；因此，當資料量 \(n\) 較小時，線性查詢反而比二分搜尋更快。