Skip to content

8.2   Heap construction operation

In some cases, we want to build a heap using all elements of a list, and this process is known as "heap construction operation."

8.2.1   Implementing with heap insertion operation

First, we create an empty heap and then iterate through the list, performing the "heap insertion operation" on each element in turn. This means adding the element to the end of the heap and then "heapifying" it from bottom to top.

Each time an element is added to the heap, the length of the heap increases by one. Since nodes are added to the binary tree from top to bottom, the heap is constructed "from top to bottom."

Let the number of elements be \(n\), and each element's insertion operation takes \(O(\log{n})\) time, thus the time complexity of this heap construction method is \(O(n \log n)\).

8.2.2   Implementing by heapifying through traversal

In fact, we can implement a more efficient method of heap construction in two steps.

  1. Add all elements of the list as they are into the heap, at this point the properties of the heap are not yet satisfied.
  2. Traverse the heap in reverse order (reverse of level-order traversal), and perform "top to bottom heapify" on each non-leaf node.

After heapifying a node, the subtree with that node as the root becomes a valid sub-heap. Since the traversal is in reverse order, the heap is built "from bottom to top."

The reason for choosing reverse traversal is that it ensures the subtree below the current node is already a valid sub-heap, making the heapification of the current node effective.

It's worth mentioning that since leaf nodes have no children, they naturally form valid sub-heaps and do not need to be heapified. As shown in the following code, the last non-leaf node is the parent of the last node; we start from it and traverse in reverse order to perform heapification:

my_heap.py
def __init__(self, nums: list[int]):
    """构造方法，根据输入列表建堆"""
    # 将列表元素原封不动添加进堆
    self.max_heap = nums
    # 堆化除叶节点以外的其他所有节点
    for i in range(self.parent(self.size() - 1), -1, -1):
        self.sift_down(i)
my_heap.cpp
/* 构造方法，根据输入列表建堆 */
MaxHeap(vector<int> nums) {
    // 将列表元素原封不动添加进堆
    maxHeap = nums;
    // 堆化除叶节点以外的其他所有节点
    for (int i = parent(size() - 1); i >= 0; i--) {
        siftDown(i);
    }
}
my_heap.java
/* 构造方法，根据输入列表建堆 */
MaxHeap(List<Integer> nums) {
    // 将列表元素原封不动添加进堆
    maxHeap = new ArrayList<>(nums);
    // 堆化除叶节点以外的其他所有节点
    for (int i = parent(size() - 1); i >= 0; i--) {
        siftDown(i);
    }
}
my_heap.cs
/* 构造函数，根据输入列表建堆 */
MaxHeap(IEnumerable<int> nums) {
    // 将列表元素原封不动添加进堆
    maxHeap = new List<int>(nums);
    // 堆化除叶节点以外的其他所有节点
    var size = Parent(this.Size() - 1);
    for (int i = size; i >= 0; i--) {
        SiftDown(i);
    }
}
my_heap.go
/* 构造函数，根据切片建堆 */
func newMaxHeap(nums []any) *maxHeap {
    // 将列表元素原封不动添加进堆
    h := &maxHeap{data: nums}
    for i := h.parent(len(h.data) - 1); i >= 0; i-- {
        // 堆化除叶节点以外的其他所有节点
        h.siftDown(i)
    }
    return h
}
my_heap.swift
/* 构造方法，根据输入列表建堆 */
init(nums: [Int]) {
    // 将列表元素原封不动添加进堆
    maxHeap = nums
    // 堆化除叶节点以外的其他所有节点
    for i in (0 ... parent(i: size() - 1)).reversed() {
        siftDown(i: i)
    }
}
my_heap.js
/* 构造方法，建立空堆或根据输入列表建堆 */
constructor(nums) {
    // 将列表元素原封不动添加进堆
    this.#maxHeap = nums === undefined ? [] : [...nums];
    // 堆化除叶节点以外的其他所有节点
    for (let i = this.#parent(this.size() - 1); i >= 0; i--) {
        this.#siftDown(i);
    }
}
my_heap.ts
/* 构造方法，建立空堆或根据输入列表建堆 */
constructor(nums?: number[]) {
    // 将列表元素原封不动添加进堆
    this.maxHeap = nums === undefined ? [] : [...nums];
    // 堆化除叶节点以外的其他所有节点
    for (let i = this.parent(this.size() - 1); i >= 0; i--) {
        this.siftDown(i);
    }
}
my_heap.dart
/* 构造方法，根据输入列表建堆 */
MaxHeap(List<int> nums) {
  // 将列表元素原封不动添加进堆
  _maxHeap = nums;
  // 堆化除叶节点以外的其他所有节点
  for (int i = _parent(size() - 1); i >= 0; i--) {
    siftDown(i);
  }
}
my_heap.rs
/* 构造方法，根据输入列表建堆 */
fn new(nums: Vec<i32>) -> Self {
    // 将列表元素原封不动添加进堆
    let mut heap = MaxHeap { max_heap: nums };
    // 堆化除叶节点以外的其他所有节点
    for i in (0..=Self::parent(heap.size() - 1)).rev() {
        heap.sift_down(i);
    }
    heap
}
my_heap.c
/* 构造函数，根据切片建堆 */
MaxHeap *newMaxHeap(int nums[], int size) {
    // 所有元素入堆
    MaxHeap *maxHeap = (MaxHeap *)malloc(sizeof(MaxHeap));
    maxHeap->size = size;
    memcpy(maxHeap->data, nums, size * sizeof(int));
    for (int i = parent(maxHeap, size - 1); i >= 0; i--) {
        // 堆化除叶节点以外的其他所有节点
        siftDown(maxHeap, i);
    }
    return maxHeap;
}
my_heap.kt
/* 大顶堆 */
class MaxHeap(nums: MutableList<Int>?) {
    // 使用列表而非数组，这样无须考虑扩容问题
    private val maxHeap = mutableListOf<Int>()

    /* 构造方法，根据输入列表建堆 */
    init {
        // 将列表元素原封不动添加进堆
        maxHeap.addAll(nums!!)
        // 堆化除叶节点以外的其他所有节点
        for (i in parent(size() - 1) downTo 0) {
            siftDown(i)
        }
    }

    /* 获取左子节点的索引 */
    private fun left(i: Int): Int {
        return 2 * i + 1
    }

    /* 获取右子节点的索引 */
    private fun right(i: Int): Int {
        return 2 * i + 2
    }

    /* 获取父节点的索引 */
    private fun parent(i: Int): Int {
        return (i - 1) / 2 // 向下整除
    }

    /* 交换元素 */
    private fun swap(i: Int, j: Int) {
        val temp = maxHeap[i]
        maxHeap[i] = maxHeap[j]
        maxHeap[j] = temp
    }

    /* 获取堆大小 */
    fun size(): Int {
        return maxHeap.size
    }

    /* 判断堆是否为空 */
    fun isEmpty(): Boolean {
        /* 判断堆是否为空 */
        return size() == 0
    }

    /* 访问堆顶元素 */
    fun peek(): Int {
        return maxHeap[0]
    }

    /* 元素入堆 */
    fun push(_val: Int) {
        // 添加节点
        maxHeap.add(_val)
        // 从底至顶堆化
        siftUp(size() - 1)
    }

    /* 从节点 i 开始，从底至顶堆化 */
    private fun siftUp(it: Int) {
        // Kotlin的函数参数不可变，因此创建临时变量
        var i = it
        while (true) {
            // 获取节点 i 的父节点
            val p = parent(i)
            // 当“越过根节点”或“节点无须修复”时，结束堆化
            if (p < 0 || maxHeap[i] <= maxHeap[p]) break
            // 交换两节点
            swap(i, p)
            // 循环向上堆化
            i = p
        }
    }

    /* 元素出堆 */
    fun pop(): Int {
        // 判空处理
        if (isEmpty()) throw IndexOutOfBoundsException()
        // 交换根节点与最右叶节点（交换首元素与尾元素）
        swap(0, size() - 1)
        // 删除节点
        val _val = maxHeap.removeAt(size() - 1)
        // 从顶至底堆化
        siftDown(0)
        // 返回堆顶元素
        return _val
    }

    /* 从节点 i 开始，从顶至底堆化 */
    private fun siftDown(it: Int) {
        // Kotlin的函数参数不可变，因此创建临时变量
        var i = it
        while (true) {
            // 判断节点 i, l, r 中值最大的节点，记为 ma
            val l = left(i)
            val r = right(i)
            var ma = i
            if (l < size() && maxHeap[l] > maxHeap[ma]) ma = l
            if (r < size() && maxHeap[r] > maxHeap[ma]) ma = r
            // 若节点 i 最大或索引 l, r 越界，则无须继续堆化，跳出
            if (ma == i) break
            // 交换两节点
            swap(i, ma)
            // 循环向下堆化
            i = ma
        }
    }

    /* 打印堆（二叉树） */
    fun print() {
        val queue = PriorityQueue { a: Int, b: Int -> b - a }
        queue.addAll(maxHeap)
        printHeap(queue)
    }
}
my_heap.rb
[class]{MaxHeap}-[func]{__init__}
my_heap.zig
// 构造方法，根据输入列表建堆
fn init(self: *Self, allocator: std.mem.Allocator, nums: []const T) !void {
    if (self.max_heap != null) return;
    self.max_heap = std.ArrayList(T).init(allocator);
    // 将列表元素原封不动添加进堆
    try self.max_heap.?.appendSlice(nums);
    // 堆化除叶节点以外的其他所有节点
    var i: usize = parent(self.size() - 1) + 1;
    while (i > 0) : (i -= 1) {
        try self.siftDown(i - 1);
    }
}
Code Visualization

8.2.3   Complexity analysis

Next, let's attempt to calculate the time complexity of this second method of heap construction.

  • Assuming the number of nodes in the complete binary tree is \(n\), then the number of leaf nodes is \((n + 1) / 2\), where \(/\) is integer division. Therefore, the number of nodes that need to be heapified is \((n - 1) / 2\).
  • In the process of "top to bottom heapification," each node is heapified to the leaf nodes at most, so the maximum number of iterations is the height of the binary tree \(\log n\).

Multiplying the two, we get the time complexity of the heap construction process as \(O(n \log n)\). But this estimate is not accurate, because it does not take into account the nature of the binary tree having far more nodes at the lower levels than at the top.

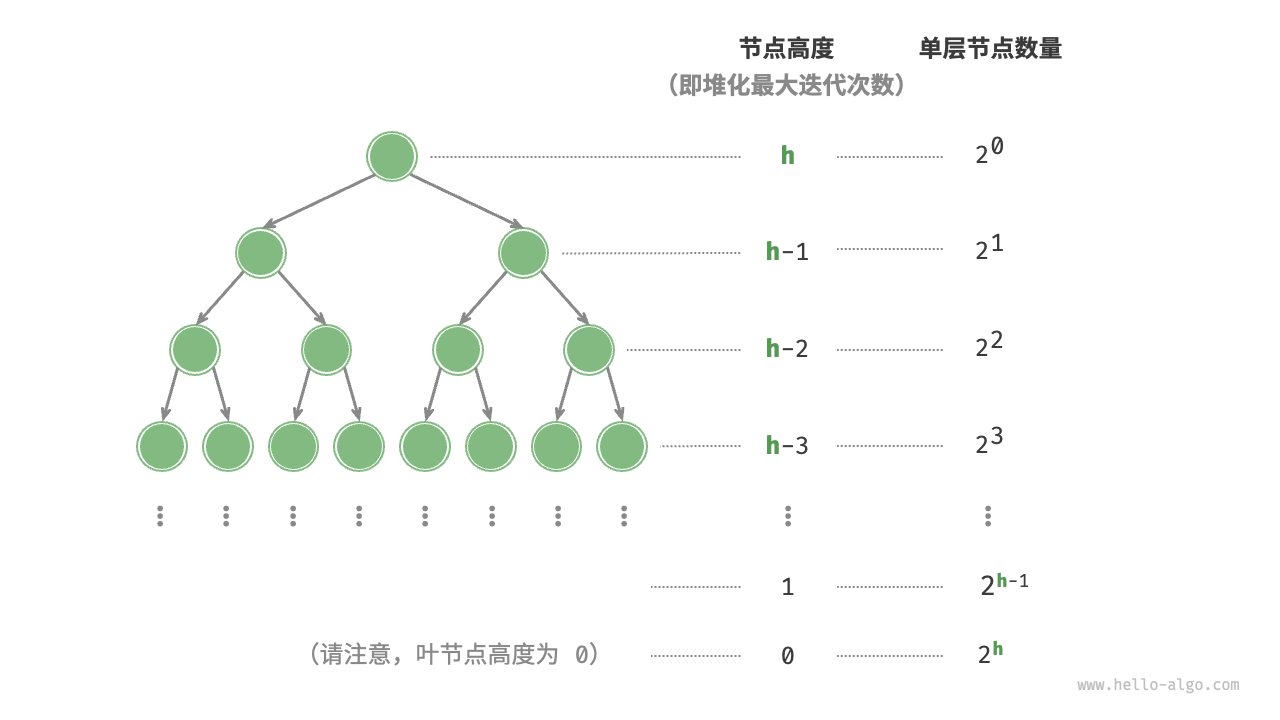
Let's perform a more accurate calculation. To simplify the calculation, assume a "perfect binary tree" with \(n\) nodes and height \(h\); this assumption does not affect the correctness of the result.

Node counts at each level of a perfect binary tree

Figure 8-5   Node counts at each level of a perfect binary tree

As shown in Figure 8-5, the maximum number of iterations for a node "to be heapified from top to bottom" is equal to the distance from that node to the leaf nodes, which is precisely "node height." Therefore, we can sum the "number of nodes \(\times\) node height" at each level, to get the total number of heapification iterations for all nodes.

\[ T(h) = 2^0h + 2^1(h-1) + 2^2(h-2) + \dots + 2^{(h-1)}\times1 \]

To simplify the above equation, we need to use knowledge of sequences from high school, first multiply \(T(h)\) by \(2\), to get:

\[ \begin{aligned} T(h) & = 2^0h + 2^1(h-1) + 2^2(h-2) + \dots + 2^{h-1}\times1 \newline 2T(h) & = 2^1h + 2^2(h-1) + 2^3(h-2) + \dots + 2^h\times1 \newline \end{aligned} \]

By subtracting \(T(h)\) from \(2T(h)\) using the method of displacement, we get:

\[ 2T(h) - T(h) = T(h) = -2^0h + 2^1 + 2^2 + \dots + 2^{h-1} + 2^h \]

Observing the equation, \(T(h)\) is an geometric series, which can be directly calculated using the sum formula, resulting in a time complexity of:

\[ \begin{aligned} T(h) & = 2 \frac{1 - 2^h}{1 - 2} - h \newline & = 2^{h+1} - h - 2 \newline & = O(2^h) \end{aligned} \]

Further, a perfect binary tree with height \(h\) has \(n = 2^{h+1} - 1\) nodes, thus the complexity is \(O(2^h) = O(n)\). This calculation shows that the time complexity of inputting a list and constructing a heap is \(O(n)\), which is very efficient.

Feel free to drop your insights, questions or suggestions