You can not select more than 25 topics
Topics must start with a letter or number, can include dashes ('-') and can be up to 35 characters long.
2.7 KiB
2.7 KiB
Top-k 問題
!!! question
給定一個長度為 $n$ 的無序陣列 `nums` ,請返回陣列中最大的 $k$ 個元素。
對於該問題,我們先介紹兩種思路比較直接的解法,再介紹效率更高的堆積解法。
方法一:走訪選擇
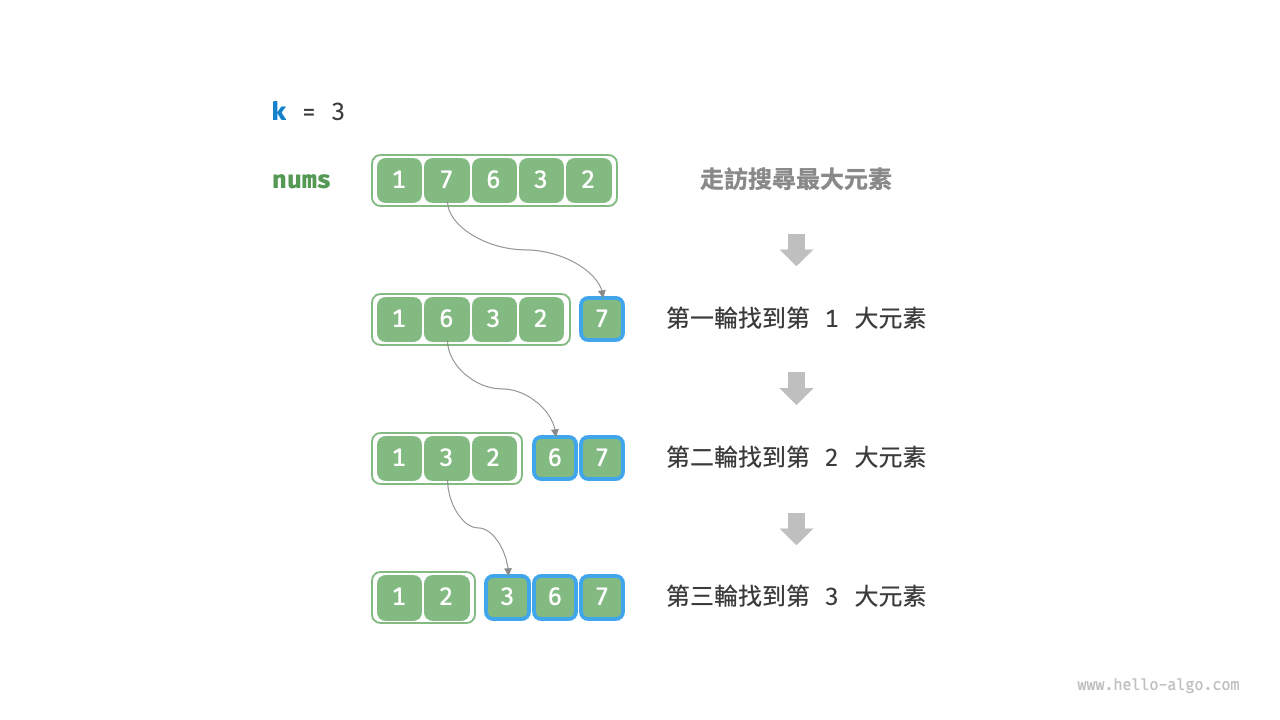
我們可以進行下圖所示的 k 輪走訪,分別在每輪中提取第 1、2、\dots、k 大的元素,時間複雜度為 O(nk) 。
此方法只適用於 k \ll n 的情況,因為當 k 與 n 比較接近時,其時間複雜度趨向於 O(n^2) ,非常耗時。
!!! tip
當 $k = n$ 時,我們可以得到完整的有序序列,此時等價於“選擇排序”演算法。
方法二:排序
如下圖所示,我們可以先對陣列 nums 進行排序,再返回最右邊的 k 個元素,時間複雜度為 O(n \log n) 。
顯然,該方法“超額”完成任務了,因為我們只需找出最大的 k 個元素即可,而不需要排序其他元素。
方法三:堆積
我們可以基於堆積更加高效地解決 Top-k 問題,流程如下圖所示。
- 初始化一個小頂堆積,其堆積頂元素最小。
- 先將陣列的前
k個元素依次入堆積。 - 從第
k + 1個元素開始,若當前元素大於堆積頂元素,則將堆積頂元素出堆積,並將當前元素入堆積。 - 走訪完成後,堆積中儲存的就是最大的
k個元素。
示例程式碼如下:
[file]{top_k}-[class]{}-[func]{top_k_heap}
總共執行了 n 輪入堆積和出堆積,堆積的最大長度為 k ,因此時間複雜度為 O(n \log k) 。該方法的效率很高,當 k 較小時,時間複雜度趨向 O(n) ;當 k 較大時,時間複雜度不會超過 O(n \log n) 。
另外,該方法適用於動態資料流的使用場景。在不斷加入資料時,我們可以持續維護堆積內的元素,從而實現最大的 k 個元素的動態更新。