11 KiB
迭代與遞迴
在演算法中,重複執行某個任務是很常見的,它與複雜度分析息息相關。因此,在介紹時間複雜度和空間複雜度之前,我們先來了解如何在程式中實現重複執行任務,即兩種基本的程式控制結構:迭代、遞迴。
迭代
迭代(iteration)是一種重複執行某個任務的控制結構。在迭代中,程式會在滿足一定的條件下重複執行某段程式碼,直到這個條件不再滿足。
for 迴圈
for 迴圈是最常見的迭代形式之一,適合在預先知道迭代次數時使用。
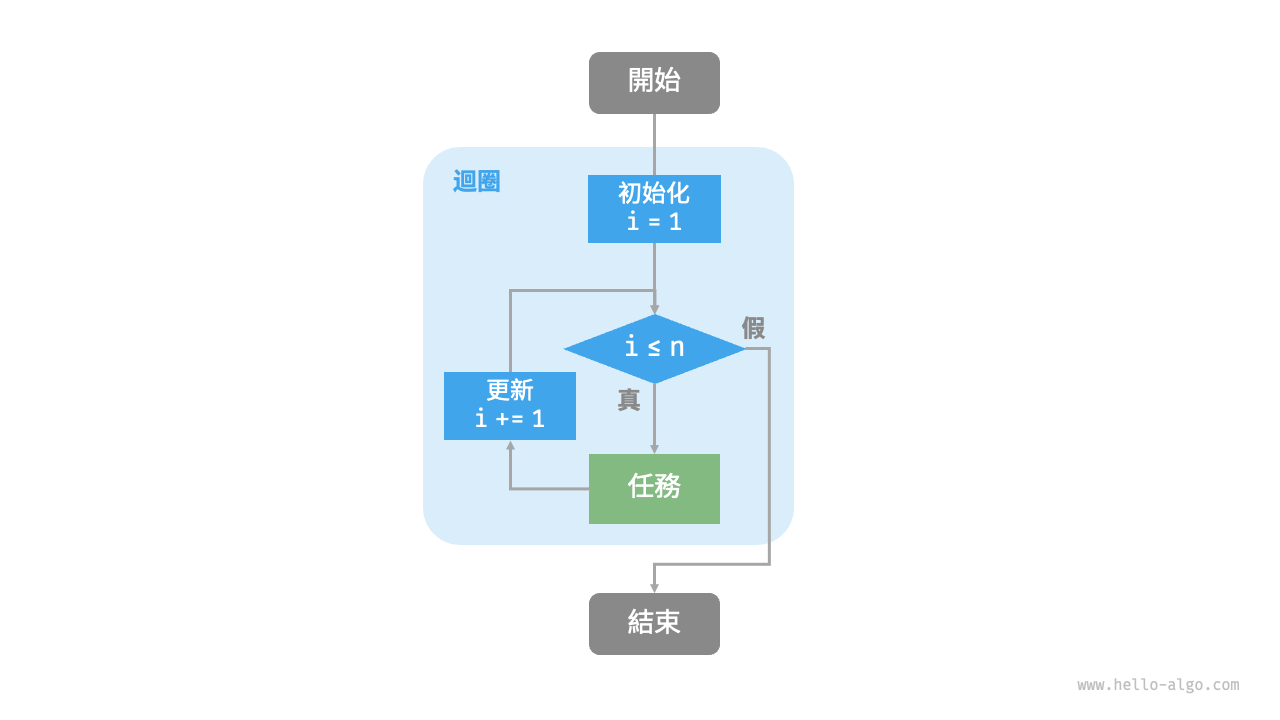
以下函式基於 for 迴圈實現了求和 1 + 2 + \dots + n ,求和結果使用變數 res 記錄。需要注意的是,Python 中 range(a, b) 對應的區間是“左閉右開”的,對應的走訪範圍為 a, a + 1, \dots, b-1 :
[file]{iteration}-[class]{}-[func]{for_loop}
下圖是該求和函式的流程框圖。
此求和函式的操作數量與輸入資料大小 n 成正比,或者說成“線性關係”。實際上,時間複雜度描述的就是這個“線性關係”。相關內容將會在下一節中詳細介紹。
while 迴圈
與 for 迴圈類似,while 迴圈也是一種實現迭代的方法。在 while 迴圈中,程式每輪都會先檢查條件,如果條件為真,則繼續執行,否則就結束迴圈。
下面我們用 while 迴圈來實現求和 1 + 2 + \dots + n :
[file]{iteration}-[class]{}-[func]{while_loop}
while 迴圈比 for 迴圈的自由度更高。在 while 迴圈中,我們可以自由地設計條件變數的初始化和更新步驟。
例如在以下程式碼中,條件變數 i 每輪進行兩次更新,這種情況就不太方便用 for 迴圈實現:
[file]{iteration}-[class]{}-[func]{while_loop_ii}
總的來說,for 迴圈的程式碼更加緊湊,while 迴圈更加靈活,兩者都可以實現迭代結構。選擇使用哪一個應該根據特定問題的需求來決定。
巢狀迴圈
我們可以在一個迴圈結構內巢狀另一個迴圈結構,下面以 for 迴圈為例:
[file]{iteration}-[class]{}-[func]{nested_for_loop}
下圖是該巢狀迴圈的流程框圖。
在這種情況下,函式的操作數量與 n^2 成正比,或者說演算法執行時間和輸入資料大小 n 成“平方關係”。
我們可以繼續新增巢狀迴圈,每一次巢狀都是一次“升維”,將會使時間複雜度提高至“立方關係”“四次方關係”,以此類推。
遞迴
遞迴(recursion)是一種演算法策略,透過函式呼叫自身來解決問題。它主要包含兩個階段。
- 遞:程式不斷深入地呼叫自身,通常傳入更小或更簡化的參數,直到達到“終止條件”。
- 迴:觸發“終止條件”後,程式從最深層的遞迴函式開始逐層返回,匯聚每一層的結果。
而從實現的角度看,遞迴程式碼主要包含三個要素。
- 終止條件:用於決定什麼時候由“遞”轉“迴”。
- 遞迴呼叫:對應“遞”,函式呼叫自身,通常輸入更小或更簡化的參數。
- 返回結果:對應“迴”,將當前遞迴層級的結果返回至上一層。
觀察以下程式碼,我們只需呼叫函式 recur(n) ,就可以完成 1 + 2 + \dots + n 的計算:
[file]{recursion}-[class]{}-[func]{recur}
下圖展示了該函式的遞迴過程。
雖然從計算角度看,迭代與遞迴可以得到相同的結果,但它們代表了兩種完全不同的思考和解決問題的範式。
- 迭代:“自下而上”地解決問題。從最基礎的步驟開始,然後不斷重複或累加這些步驟,直到任務完成。
- 遞迴:“自上而下”地解決問題。將原問題分解為更小的子問題,這些子問題和原問題具有相同的形式。接下來將子問題繼續分解為更小的子問題,直到基本情況時停止(基本情況的解是已知的)。
以上述求和函式為例,設問題 f(n) = 1 + 2 + \dots + n 。
- 迭代:在迴圈中模擬求和過程,從
1走訪到n,每輪執行求和操作,即可求得f(n)。 - 遞迴:將問題分解為子問題
f(n) = n + f(n-1),不斷(遞迴地)分解下去,直至基本情況f(1) = 1時終止。
呼叫堆疊
遞迴函式每次呼叫自身時,系統都會為新開啟的函式分配記憶體,以儲存區域性變數、呼叫位址和其他資訊等。這將導致兩方面的結果。
- 函式的上下文資料都儲存在稱為“堆疊幀空間”的記憶體區域中,直至函式返回後才會被釋放。因此,遞迴通常比迭代更加耗費記憶體空間。
- 遞迴呼叫函式會產生額外的開銷。因此遞迴通常比迴圈的時間效率更低。
如下圖所示,在觸發終止條件前,同時存在 n 個未返回的遞迴函式,遞迴深度為 n 。
在實際中,程式語言允許的遞迴深度通常是有限的,過深的遞迴可能導致堆疊溢位錯誤。
尾遞迴
有趣的是,如果函式在返回前的最後一步才進行遞迴呼叫,則該函式可以被編譯器或直譯器最佳化,使其在空間效率上與迭代相當。這種情況被稱為尾遞迴(tail recursion)。
- 普通遞迴:當函式返回到上一層級的函式後,需要繼續執行程式碼,因此系統需要儲存上一層呼叫的上下文。
- 尾遞迴:遞迴呼叫是函式返回前的最後一個操作,這意味著函式返回到上一層級後,無須繼續執行其他操作,因此系統無須儲存上一層函式的上下文。
以計算 1 + 2 + \dots + n 為例,我們可以將結果變數 res 設為函式參數,從而實現尾遞迴:
[file]{recursion}-[class]{}-[func]{tail_recur}
尾遞迴的執行過程如下圖所示。對比普通遞迴和尾遞迴,兩者的求和操作的執行點是不同的。
- 普通遞迴:求和操作是在“迴”的過程中執行的,每層返回後都要再執行一次求和操作。
- 尾遞迴:求和操作是在“遞”的過程中執行的,“迴”的過程只需層層返回。
!!! tip
請注意,許多編譯器或直譯器並不支持尾遞迴最佳化。例如,Python 預設不支持尾遞迴最佳化,因此即使函式是尾遞迴形式,仍然可能會遇到堆疊溢位問題。
遞迴樹
當處理與“分治”相關的演算法問題時,遞迴往往比迭代的思路更加直觀、程式碼更加易讀。以“費波那契數列”為例。
!!! question
給定一個費波那契數列 $0, 1, 1, 2, 3, 5, 8, 13, \dots$ ,求該數列的第 $n$ 個數字。
設費波那契數列的第 n 個數字為 f(n) ,易得兩個結論。
- 數列的前兩個數字為
f(1) = 0和f(2) = 1。 - 數列中的每個數字是前兩個數字的和,即
f(n) = f(n - 1) + f(n - 2)。
按照遞推關係進行遞迴呼叫,將前兩個數字作為終止條件,便可寫出遞迴程式碼。呼叫 fib(n) 即可得到費波那契數列的第 n 個數字:
[file]{recursion}-[class]{}-[func]{fib}
觀察以上程式碼,我們在函式內遞迴呼叫了兩個函式,這意味著從一個呼叫產生了兩個呼叫分支。如下圖所示,這樣不斷遞迴呼叫下去,最終將產生一棵層數為 n 的遞迴樹(recursion tree)。
從本質上看,遞迴體現了“將問題分解為更小子問題”的思維範式,這種分治策略至關重要。
- 從演算法角度看,搜尋、排序、回溯、分治、動態規劃等許多重要演算法策略直接或間接地應用了這種思維方式。
- 從資料結構角度看,遞迴天然適合處理鏈結串列、樹和圖的相關問題,因為它們非常適合用分治思想進行分析。
兩者對比
總結以上內容,如下表所示,迭代和遞迴在實現、效能和適用性上有所不同。
表 迭代與遞迴特點對比
| 迭代 | 遞迴 | |
|---|---|---|
| 實現方式 | 迴圈結構 | 函式呼叫自身 |
| 時間效率 | 效率通常較高,無函式呼叫開銷 | 每次函式呼叫都會產生開銷 |
| 記憶體使用 | 通常使用固定大小的記憶體空間 | 累積函式呼叫可能使用大量的堆疊幀空間 |
| 適用問題 | 適用於簡單迴圈任務,程式碼直觀、可讀性好 | 適用於子問題分解,如樹、圖、分治、回溯等,程式碼結構簡潔、清晰 |
!!! tip
如果感覺以下內容理解困難,可以在讀完“堆疊”章節後再來複習。
那麼,迭代和遞迴具有什麼內在關聯呢?以上述遞迴函式為例,求和操作在遞迴的“迴”階段進行。這意味著最初被呼叫的函式實際上是最後完成其求和操作的,這種工作機制與堆疊的“先入後出”原則異曲同工。
事實上,“呼叫堆疊”和“堆疊幀空間”這類遞迴術語已經暗示了遞迴與堆疊之間的密切關係。
- 遞:當函式被呼叫時,系統會在“呼叫堆疊”上為該函式分配新的堆疊幀,用於儲存函式的區域性變數、參數、返回位址等資料。
- 迴:當函式完成執行並返回時,對應的堆疊幀會被從“呼叫堆疊”上移除,恢復之前函式的執行環境。
因此,我們可以使用一個顯式的堆疊來模擬呼叫堆疊的行為,從而將遞迴轉化為迭代形式:
[file]{recursion}-[class]{}-[func]{for_loop_recur}
觀察以上程式碼,當遞迴轉化為迭代後,程式碼變得更加複雜了。儘管迭代和遞迴在很多情況下可以互相轉化,但不一定值得這樣做,有以下兩點原因。
- 轉化後的程式碼可能更加難以理解,可讀性更差。
- 對於某些複雜問題,模擬系統呼叫堆疊的行為可能非常困難。
總之,選擇迭代還是遞迴取決於特定問題的性質。在程式設計實踐中,權衡兩者的優劣並根據情境選擇合適的方法至關重要。