20 KiB

Raw Blame History Unescape Escape

comments
true

堆

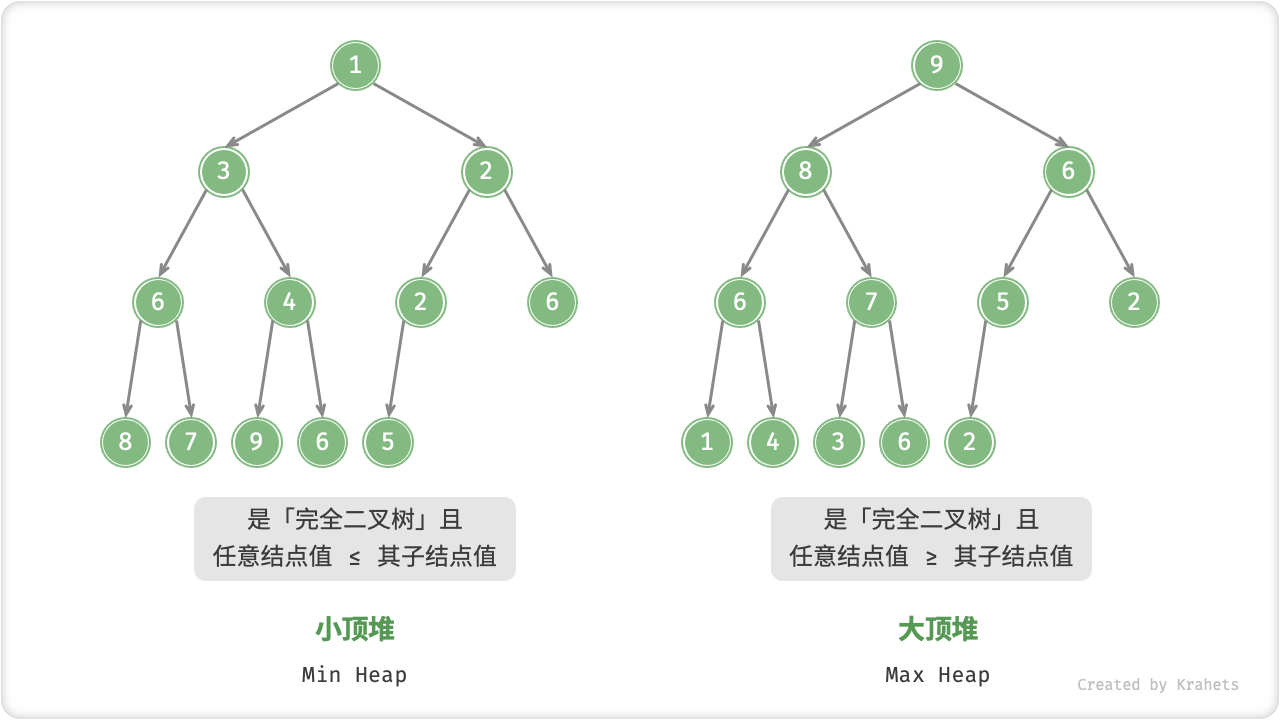
「堆 Heap」是一棵限定条件下的「完全二叉树」。根据成立条件，堆主要分为两种类型：

「大顶堆 Max Heap」，任意结点的值 \geq 其子结点的值；
「小顶堆 Min Heap」，任意结点的值 \leq 其子结点的值；

堆术语与性质

由于堆是完全二叉树，因此最底层结点靠左填充，其它层结点皆被填满。
二叉树中的根结点对应「堆顶」，底层最靠右结点对应「堆底」。
对于大顶堆 / 小顶堆，其堆顶元素（即根结点）的值最大 / 最小。

堆常用操作

值得说明的是，多数编程语言提供的是「优先队列 Priority Queue」，其是一种抽象数据结构，定义为具有出队优先级的队列。

而恰好，堆的定义与优先队列的操作逻辑完全吻合，大顶堆就是一个元素从大到小出队的优先队列。从使用角度看，我们可以将「优先队列」和「堆」理解为等价的数据结构。因此，本文与代码对两者不做特别区分，统一使用「堆」来命名。

堆的常用操作见下表（方法命名以 Java 为例）。

Table. 堆的常用操作

方法	描述	时间复杂度
add()	元素入堆	`O(\log n)`
poll()	堆顶元素出堆	`O(\log n)`
peek()	访问堆顶元素（大 / 小顶堆分别为最大 / 小值）	`O(1)`
size()	获取堆的元素数量	`O(1)`
isEmpty()	判断堆是否为空	`O(1)`

我们可以直接使用编程语言提供的堆类（或优先队列类）。

!!! tip

类似于排序中“从小到大排列”和“从大到小排列”，“大顶堆”和“小顶堆”可仅通过修改 Comparator 来互相转换。

=== "Java"

```java title="heap.java"
/* 初始化堆 */
// 初始化小顶堆
Queue<Integer> minHeap = new PriorityQueue<>();
// 初始化大顶堆（使用 lambda 表达式修改 Comparator 即可）
Queue<Integer> maxHeap = new PriorityQueue<>((a, b) -> { return b - a; });

/* 元素入堆 */
maxHeap.add(1);
maxHeap.add(3);
maxHeap.add(2);
maxHeap.add(5);
maxHeap.add(4);

/* 获取堆顶元素 */
int peek = maxHeap.peek(); // 5

/* 堆顶元素出堆 */
// 出堆元素会形成一个从大到小的序列
peek = heap.poll();  // 5
peek = heap.poll();  // 4
peek = heap.poll();  // 3
peek = heap.poll();  // 2
peek = heap.poll();  // 1

/* 获取堆大小 */
int size = maxHeap.size();

/* 判断堆是否为空 */
boolean isEmpty = maxHeap.isEmpty();

/* 输入列表并建堆 */
minHeap = new PriorityQueue<>(Arrays.asList(1, 3, 2, 5, 4));
```

=== "C++"

```cpp title="heap.cpp"
/* 初始化堆 */
// 初始化小顶堆
priority_queue<int, vector<int>, greater<int>> minHeap;
// 初始化大顶堆
priority_queue<int, vector<int>, less<int>> maxHeap;

/* 元素入堆 */
maxHeap.push(1);
maxHeap.push(3);
maxHeap.push(2);
maxHeap.push(5);
maxHeap.push(4);

/* 获取堆顶元素 */
int peek = maxHeap.top(); // 5

/* 堆顶元素出堆 */
// 出堆元素会形成一个从大到小的序列
maxHeap.pop(); // 5
maxHeap.pop(); // 4
maxHeap.pop(); // 3
maxHeap.pop(); // 2
maxHeap.pop(); // 1

/* 获取堆大小 */
int size = maxHeap.size();

/* 判断堆是否为空 */
bool isEmpty = maxHeap.empty();

/* 输入列表并建堆 */
vector<int> input{1, 3, 2, 5, 4};
priority_queue<int, vector<int>, greater<int>> minHeap(input.begin(), input.end());
```

=== "Python"

```python title="heap.py"

```

=== "Go"

```go title="heap.go"
// Go 语言中可以通过实现 heap.Interface 来构建整数大顶堆
// 实现 heap.Interface 需要同时实现 sort.Interface
type intHeap []any

// Push heap.Interface 的方法，实现推入元素到堆
func (h *intHeap) Push(x any) {
    // Push 和 Pop 使用 pointer receiver 作为参数
    // 因为它们不仅会对切片的内容进行调整，还会修改切片的长度。
    *h = append(*h, x.(int))
}

// Pop heap.Interface 的方法，实现弹出堆顶元素
func (h *intHeap) Pop() any {
    // 待出堆元素存放在最后
    last := (*h)[len(*h)-1]
    *h = (*h)[:len(*h)-1]
    return last
}

// Len sort.Interface 的方法
func (h *intHeap) Len() int {
    return len(*h)
}

// Less sort.Interface 的方法
func (h *intHeap) Less(i, j int) bool {
    // 如果实现小顶堆，则需要调整为小于号
    return (*h)[i].(int) > (*h)[j].(int)
}

// Swap sort.Interface 的方法
func (h *intHeap) Swap(i, j int) {
    (*h)[i], (*h)[j] = (*h)[j], (*h)[i]
}

// Top 获取堆顶元素
func (h *intHeap) Top() any {
    return (*h)[0]
}

/* Driver Code */
func TestHeap(t *testing.T) {
    /* 初始化堆 */
    // 初始化大顶堆
    maxHeap := &intHeap{}
    heap.Init(maxHeap)
    /* 元素入堆 */
    // 调用 heap.Interface 的方法，来添加元素
    heap.Push(maxHeap, 1)
    heap.Push(maxHeap, 3)
    heap.Push(maxHeap, 2)
    heap.Push(maxHeap, 4)
    heap.Push(maxHeap, 5)

    /* 获取堆顶元素 */
    top := maxHeap.Top()
    fmt.Printf("堆顶元素为 %d\n", top)

    /* 堆顶元素出堆 */
    // 调用 heap.Interface 的方法，来移除元素
    heap.Pop(maxHeap)
    heap.Pop(maxHeap)
    heap.Pop(maxHeap)
    heap.Pop(maxHeap)
    heap.Pop(maxHeap)

    /* 获取堆大小 */
    size := len(*maxHeap)
    fmt.Printf("堆元素数量为 %d\n", size)

    /* 判断堆是否为空 */
    isEmpty := len(*maxHeap) == 0
    fmt.Printf("堆是否为空 %t\n", isEmpty)
}
```

=== "JavaScript"

```javascript title="heap.js"
// JavaScript 未提供内置 heap 类
```

=== "TypeScript"

```typescript title="heap.ts"
// TypeScript 未提供内置堆 Heap 类
```

=== "C"

```c title="heap.c"

```

=== "C#"

```csharp title="heap.cs"
/* 初始化堆 */
// 初始化小顶堆
PriorityQueue<int, int> minHeap = new PriorityQueue<int, int>();
// 初始化大顶堆（使用 lambda 表达式修改 Comparator 即可）
PriorityQueue<int, int> maxHeap = new PriorityQueue<int, int>(Comparer<int>.Create((x, y) => y - x));

/* 元素入堆 */
maxHeap.Enqueue(1, 1);
maxHeap.Enqueue(3, 3);
maxHeap.Enqueue(2, 2);
maxHeap.Enqueue(5, 5);
maxHeap.Enqueue(4, 4);

/* 获取堆顶元素 */
int peek = maxHeap.Peek();//5

/* 堆顶元素出堆 */
// 出堆元素会形成一个从大到小的序列
peek = maxHeap.Dequeue();  // 5
peek = maxHeap.Dequeue();  // 4
peek = maxHeap.Dequeue();  // 3
peek = maxHeap.Dequeue();  // 2
peek = maxHeap.Dequeue();  // 1

/* 获取堆大小 */
int size = maxHeap.Count;

/* 判断堆是否为空 */
bool isEmpty = maxHeap.Count == 0;

/* 输入列表并建堆 */
minHeap = new PriorityQueue<int, int>(new List<(int, int)> { (1, 1), (3, 3), (2, 2), (5, 5), (4, 4), });
```

=== "Swift"

```swift title="heap.swift"
// Swift 未提供内置 heap 类
```

=== "Zig"

```zig title="heap.zig"

```

堆的实现

下文实现的是「大顶堆」，若想转换为「小顶堆」，将所有大小逻辑判断取逆（例如将 \geq 替换为 \leq ）即可，有兴趣的同学可自行实现。

堆的存储与表示

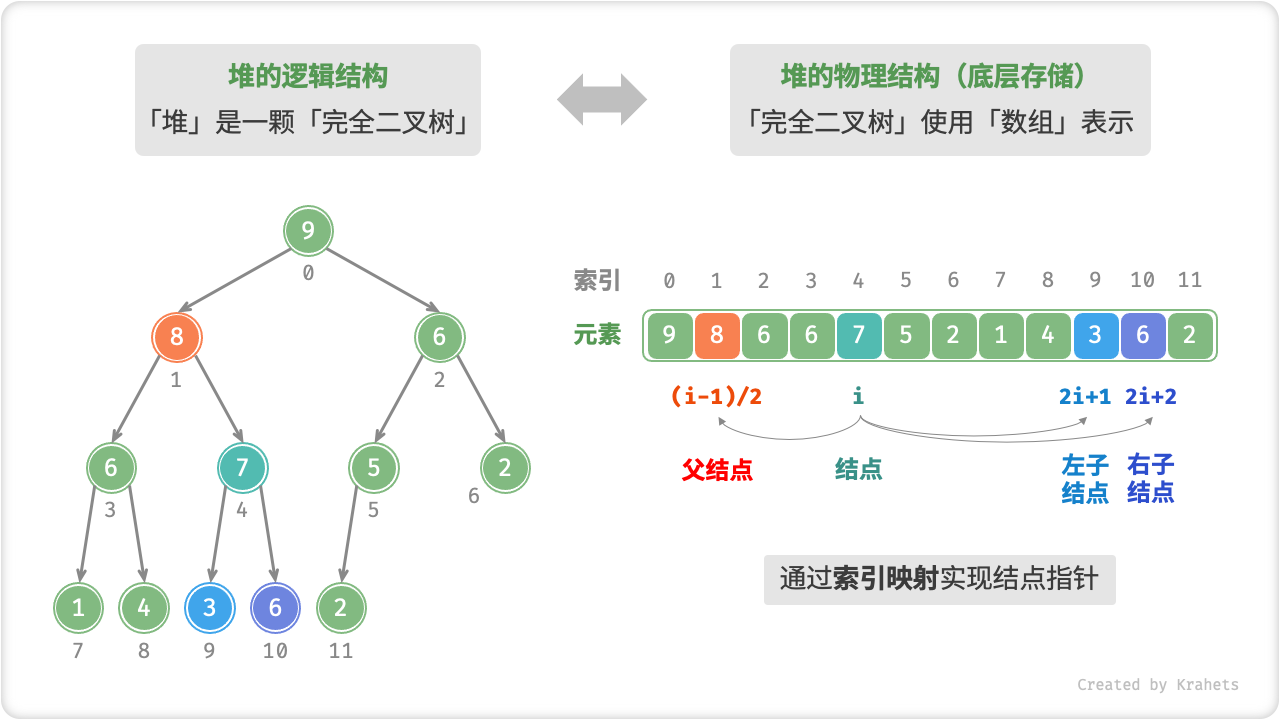
在二叉树章节我们学过，「完全二叉树」非常适合使用「数组」来表示，而堆恰好是一棵完全二叉树，因而我们采用「数组」来存储「堆」。

二叉树指针。使用数组表示二叉树时，元素代表结点值，索引代表结点在二叉树中的位置，而结点指针通过索引映射公式来实现。

具体地，给定索引 i ，那么其左子结点索引为 2i + 1 、右子结点索引为 2i + 2 、父结点索引为 (i - 1) / 2 （向下整除）。当索引越界时，代表空结点或结点不存在。

我们将索引映射公式封装成函数，以便后续使用。

=== "Java"

```java title="my_heap.java"
[class]{MaxHeap}-[func]{left}

[class]{MaxHeap}-[func]{right}

[class]{MaxHeap}-[func]{parent}
```

=== "C++"

```cpp title="my_heap.cpp"
[class]{MaxHeap}-[func]{left}

[class]{MaxHeap}-[func]{right}

[class]{MaxHeap}-[func]{parent}
```

=== "Python"

```python title="my_heap.py"

```

=== "Go"

```go title="my_heap.go"
[class]{maxHeap}-[func]{left}

[class]{maxHeap}-[func]{right}

[class]{maxHeap}-[func]{parent}
```

=== "JavaScript"

```javascript title="my_heap.js"
[class]{MaxHeap}-[func]{#left}

[class]{MaxHeap}-[func]{#right}

[class]{MaxHeap}-[func]{#parent}
```

=== "TypeScript"

```typescript title="my_heap.ts"
[class]{MaxHeap}-[func]{left}

[class]{MaxHeap}-[func]{right}

[class]{MaxHeap}-[func]{parent}
```

=== "C"

```c title="my_heap.c"
[class]{maxHeap}-[func]{left}

[class]{maxHeap}-[func]{right}

[class]{maxHeap}-[func]{parent}
```

=== "C#"

```csharp title="my_heap.cs"
[class]{MaxHeap}-[func]{left}

[class]{MaxHeap}-[func]{right}

[class]{MaxHeap}-[func]{parent}
```

=== "Swift"

```swift title="my_heap.swift"
[class]{MaxHeap}-[func]{left}

[class]{MaxHeap}-[func]{right}

[class]{MaxHeap}-[func]{parent}
```

=== "Zig"

```zig title="my_heap.zig"
[class]{MaxHeap}-[func]{left}

[class]{MaxHeap}-[func]{right}

[class]{MaxHeap}-[func]{parent}
```

访问堆顶元素

堆顶元素是二叉树的根结点，即列表首元素。

=== "Java"

```java title="my_heap.java"
[class]{MaxHeap}-[func]{peek}
```

=== "C++"

```cpp title="my_heap.cpp"
[class]{MaxHeap}-[func]{peek}
```

=== "Python"

```python title="my_heap.py"

```

=== "Go"

```go title="my_heap.go"
[class]{maxHeap}-[func]{peek}
```

=== "JavaScript"

```javascript title="my_heap.js"
[class]{MaxHeap}-[func]{peek}
```

=== "TypeScript"

```typescript title="my_heap.ts"
[class]{MaxHeap}-[func]{peek}
```

=== "C"

```c title="my_heap.c"
[class]{maxHeap}-[func]{peek}
```

=== "C#"

```csharp title="my_heap.cs"
[class]{MaxHeap}-[func]{peek}
```

=== "Swift"

```swift title="my_heap.swift"
[class]{MaxHeap}-[func]{peek}
```

=== "Zig"

```zig title="my_heap.zig"
[class]{MaxHeap}-[func]{peek}
```

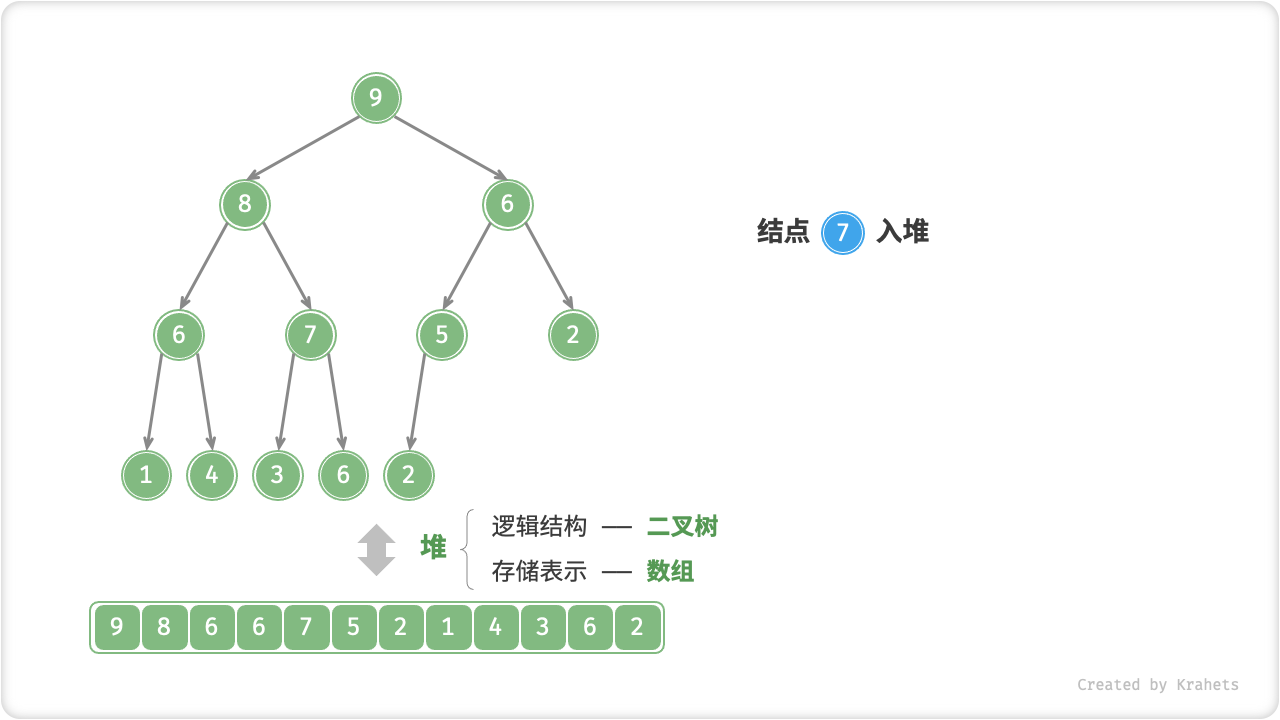
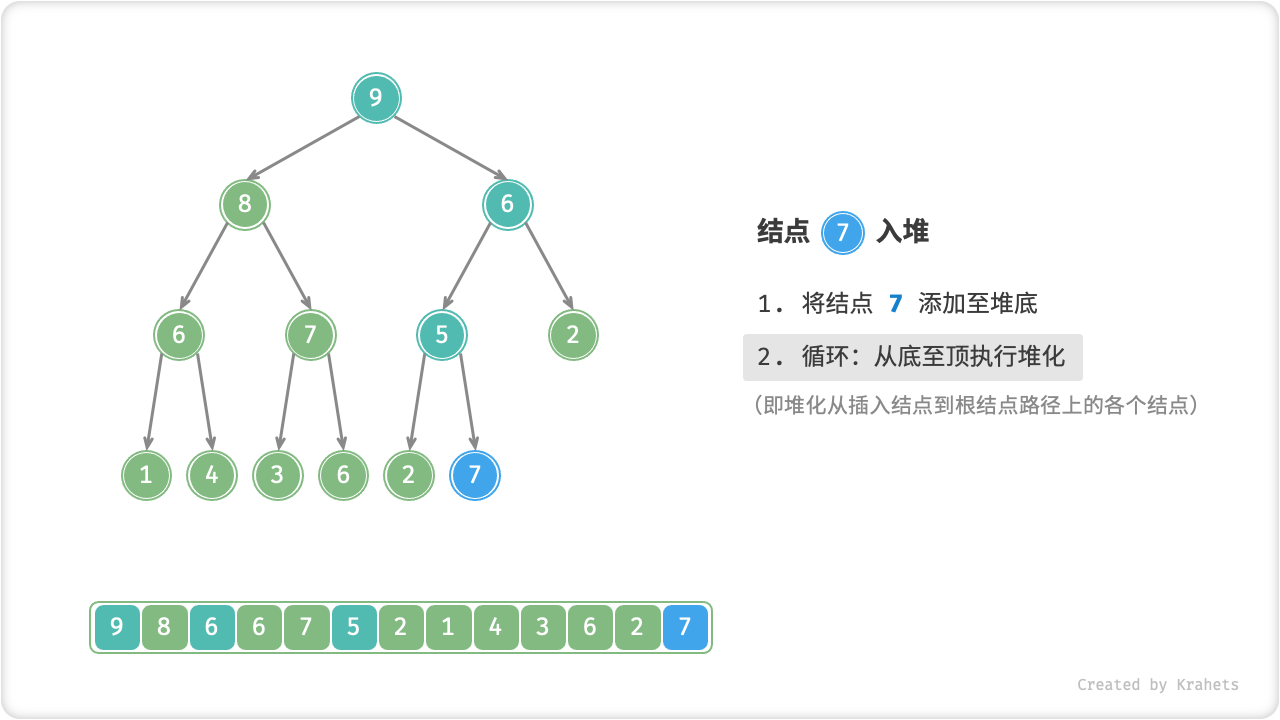
元素入堆

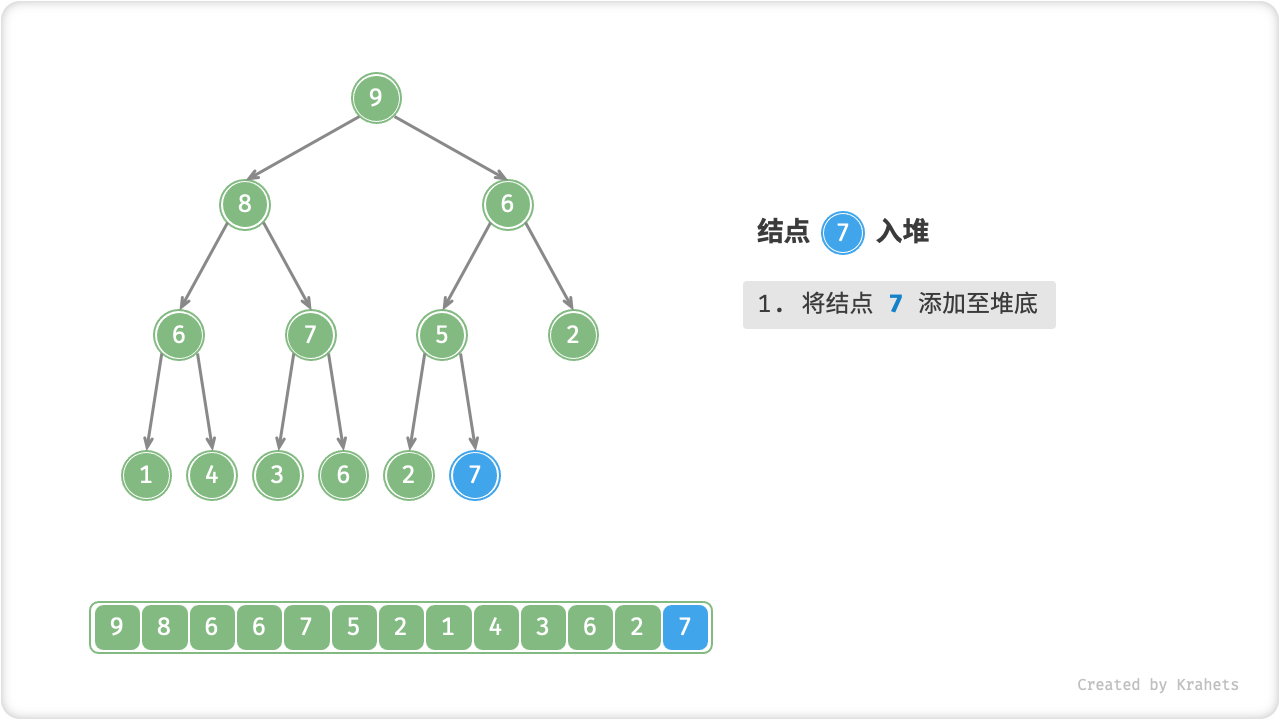
给定元素 val ，我们先将其添加到堆底。添加后，由于 val 可能大于堆中其它元素，此时堆的成立条件可能已经被破坏，因此需要修复从插入结点到根结点这条路径上的各个结点，该操作被称为「堆化 Heapify」。

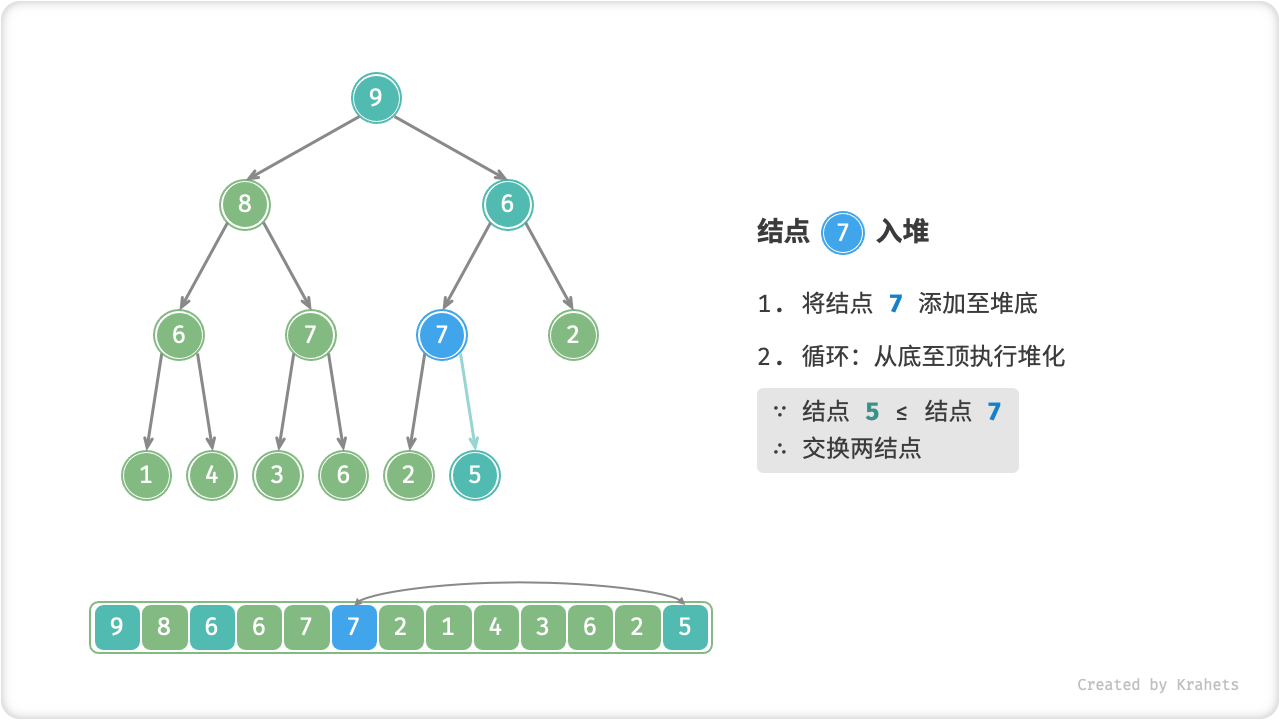
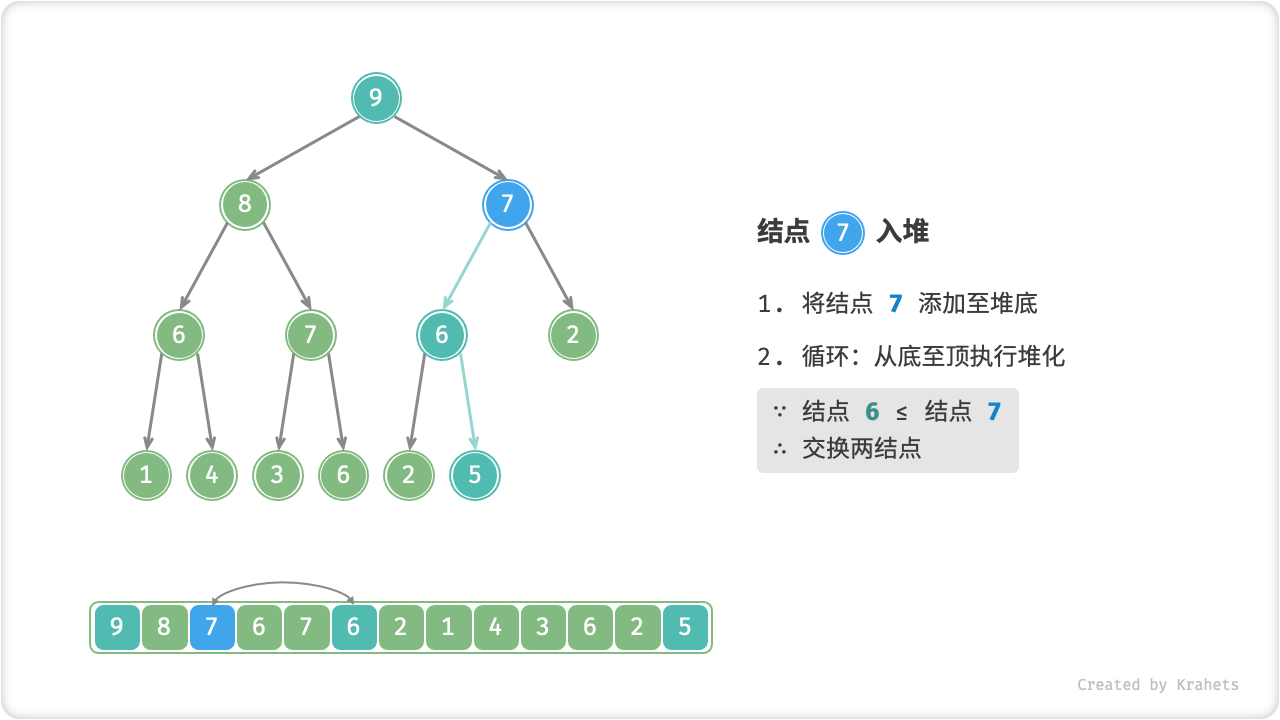
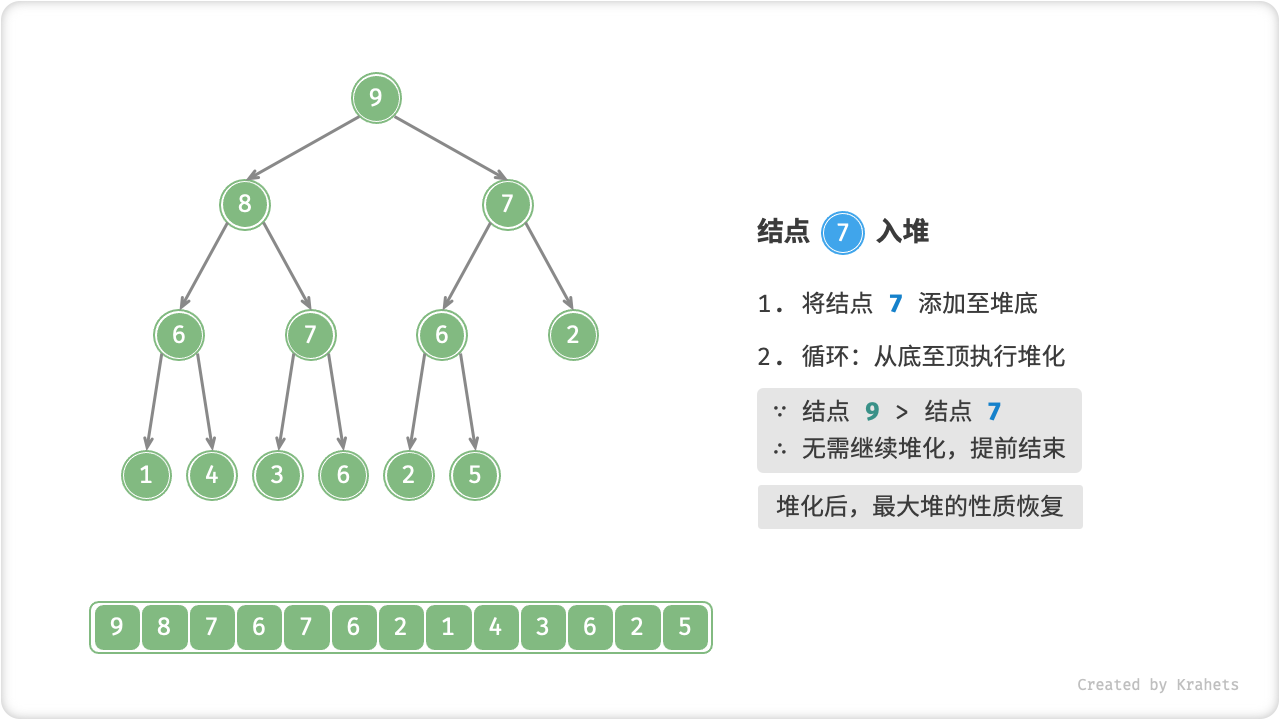
考虑从入堆结点开始，从底至顶执行堆化。具体地，比较插入结点与其父结点的值，若插入结点更大则将它们交换；并循环以上操作，从底至顶地修复堆中的各个结点；直至越过根结点时结束，或当遇到无需交换的结点时提前结束。

=== "Step 1"

=== "Step 2"

=== "Step 3"

=== "Step 4"

=== "Step 5"

=== "Step 6"

设结点总数为 n ，则树的高度为 O(\log n) ，易得堆化操作的循环轮数最多为 O(\log n) ，因而元素入堆操作的时间复杂度为 O(\log n) 。

=== "Java"

```java title="my_heap.java"
[class]{MaxHeap}-[func]{push}

[class]{MaxHeap}-[func]{siftUp}
```

=== "C++"

```cpp title="my_heap.cpp"
[class]{MaxHeap}-[func]{push}

[class]{MaxHeap}-[func]{siftUp}
```

=== "Python"

```python title="my_heap.py"

```

=== "Go"

```go title="my_heap.go"
[class]{maxHeap}-[func]{push}

[class]{maxHeap}-[func]{siftUp}
```

=== "JavaScript"

```javascript title="my_heap.js"
[class]{MaxHeap}-[func]{push}

[class]{MaxHeap}-[func]{#siftUp}
```

=== "TypeScript"

```typescript title="my_heap.ts"
[class]{MaxHeap}-[func]{push}

[class]{MaxHeap}-[func]{siftUp}
```

=== "C"

```c title="my_heap.c"
[class]{maxHeap}-[func]{push}

[class]{maxHeap}-[func]{siftUp}
```

=== "C#"

```csharp title="my_heap.cs"
[class]{MaxHeap}-[func]{push}

[class]{MaxHeap}-[func]{siftUp}
```

=== "Swift"

```swift title="my_heap.swift"
[class]{MaxHeap}-[func]{push}

[class]{MaxHeap}-[func]{siftUp}
```

=== "Zig"

```zig title="my_heap.zig"
[class]{MaxHeap}-[func]{push}

[class]{MaxHeap}-[func]{siftUp}
```

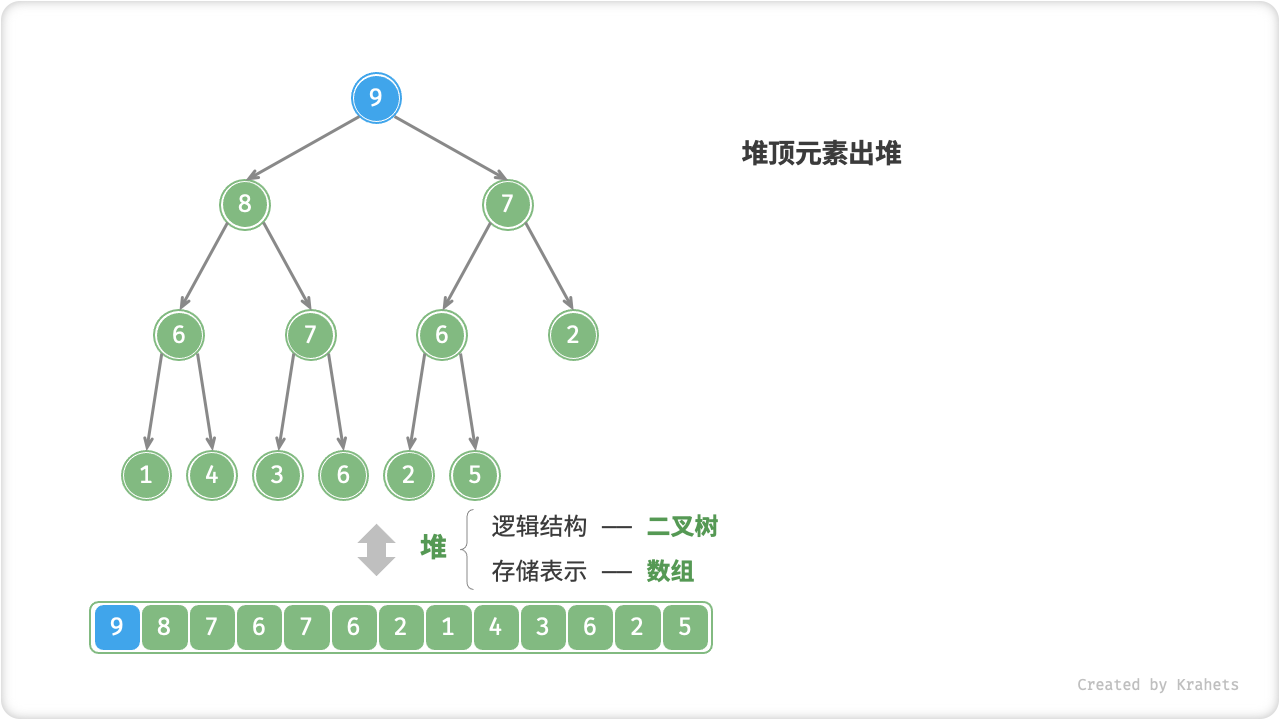
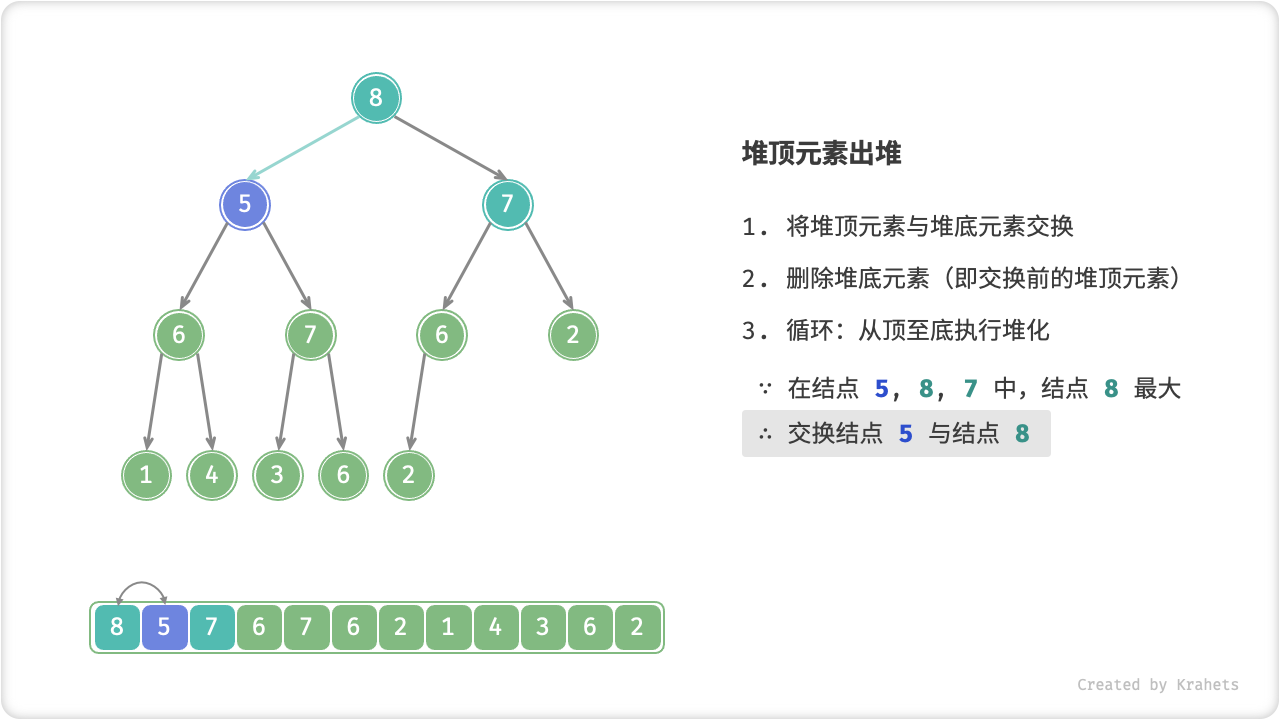
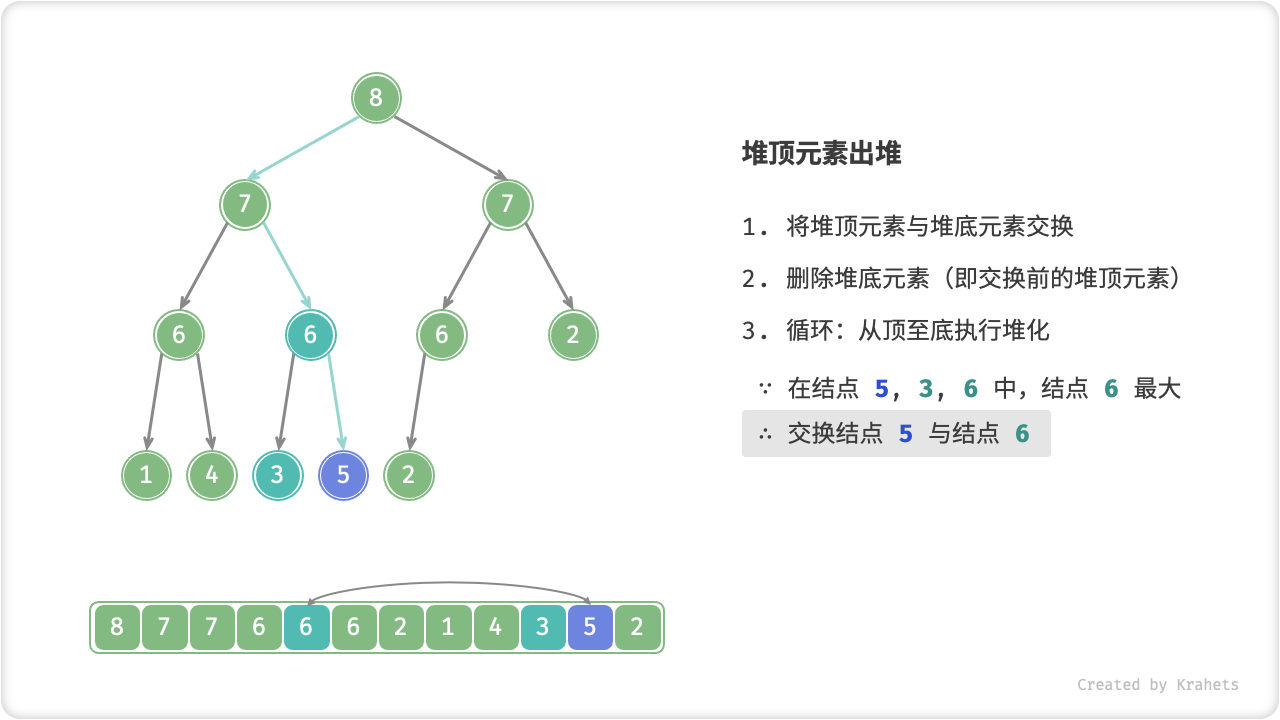
堆顶元素出堆

堆顶元素是二叉树根结点，即列表首元素，如果我们直接将首元素从列表中删除，则二叉树中所有结点都会随之发生移位（索引发生变化），这样后续使用堆化修复就很麻烦了。为了尽量减少元素索引变动，采取以下操作步骤：

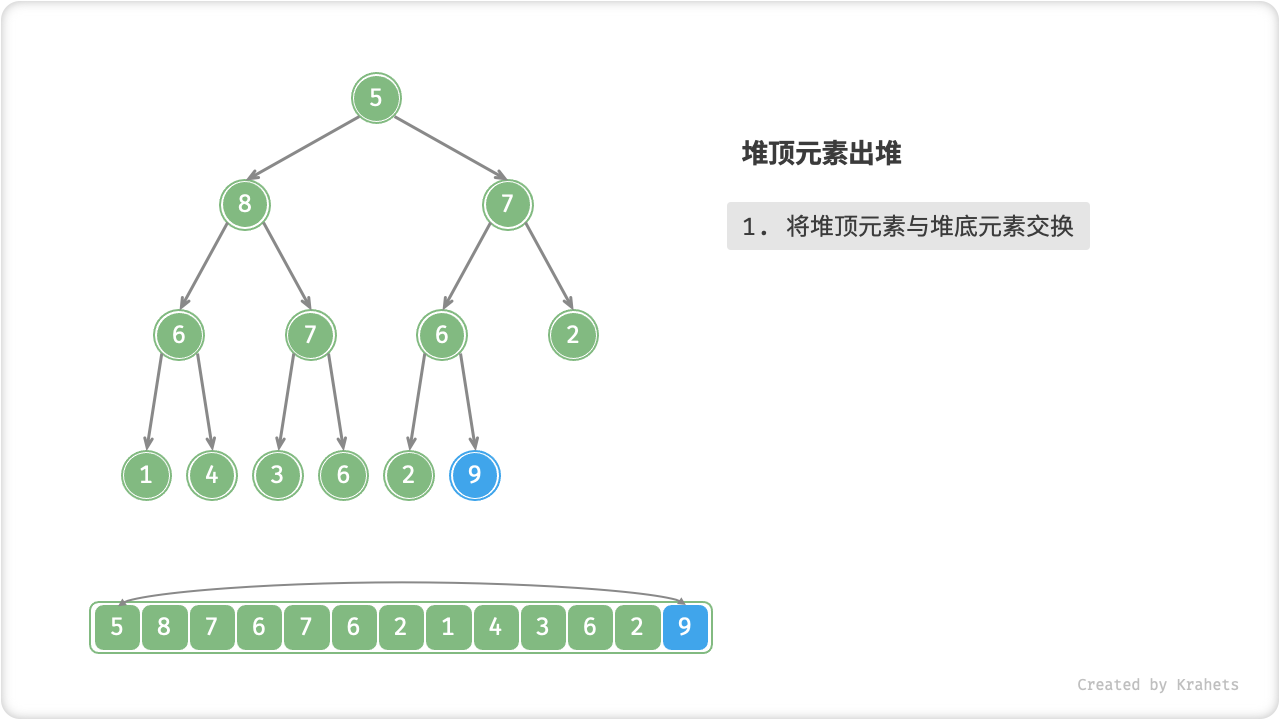
交换堆顶元素与堆底元素（即交换根结点与最右叶结点）；
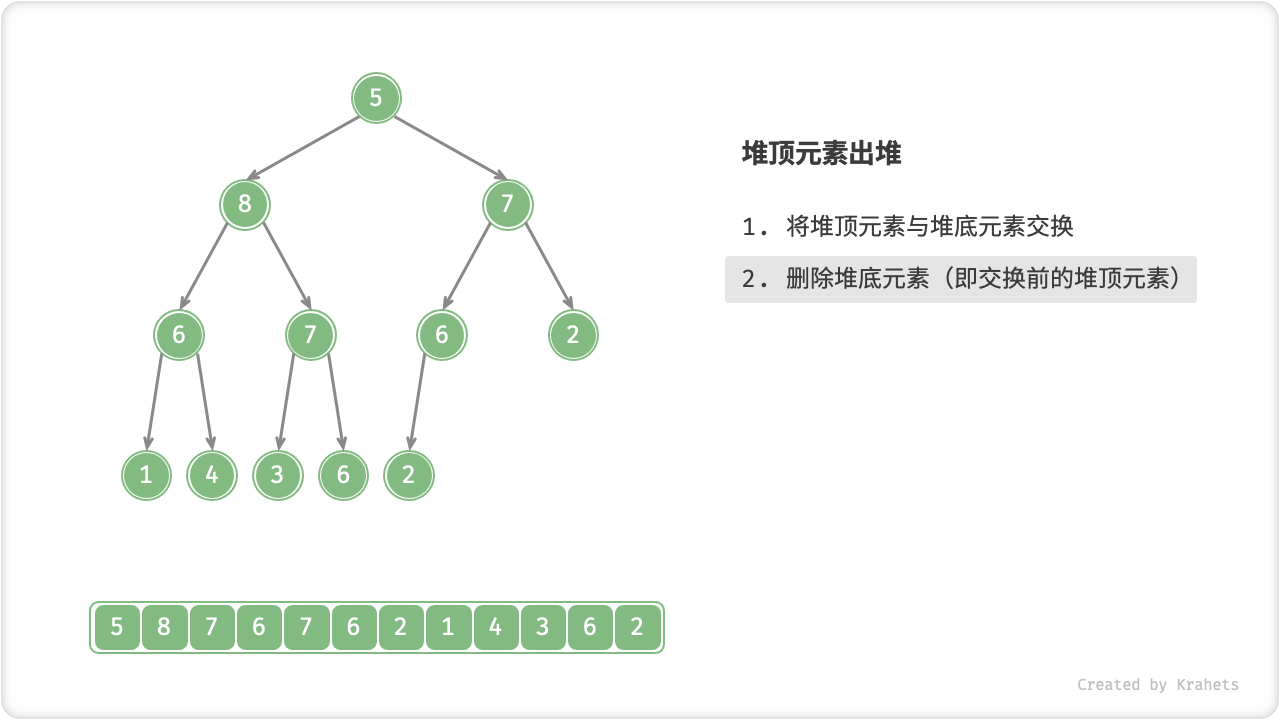
交换完成后，将堆底从列表中删除（注意，因为已经交换，实际上删除的是原来的堆顶元素）；
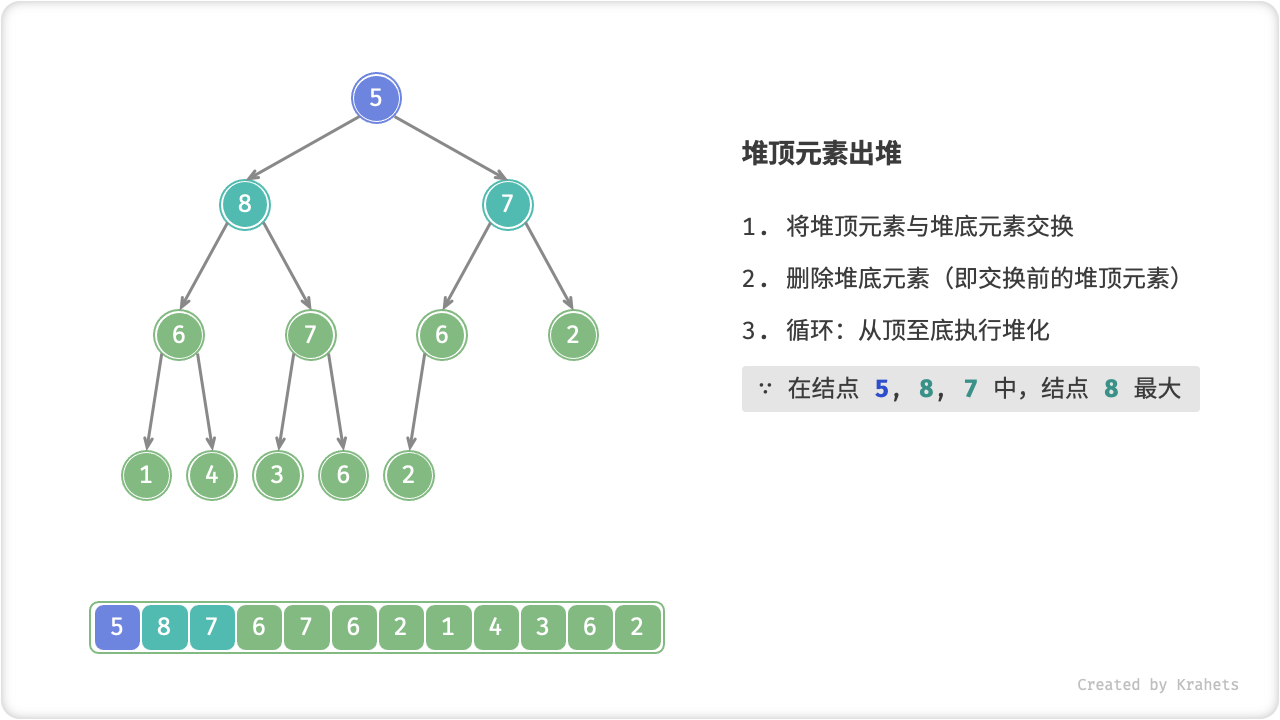
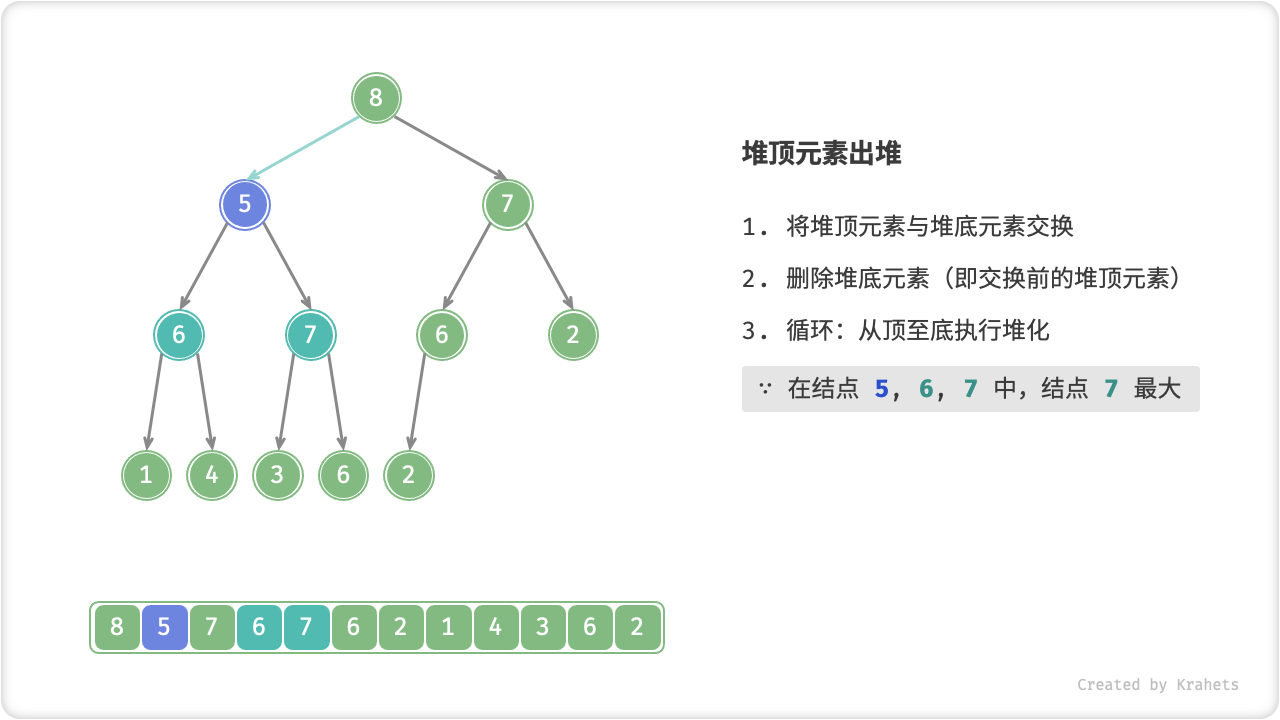
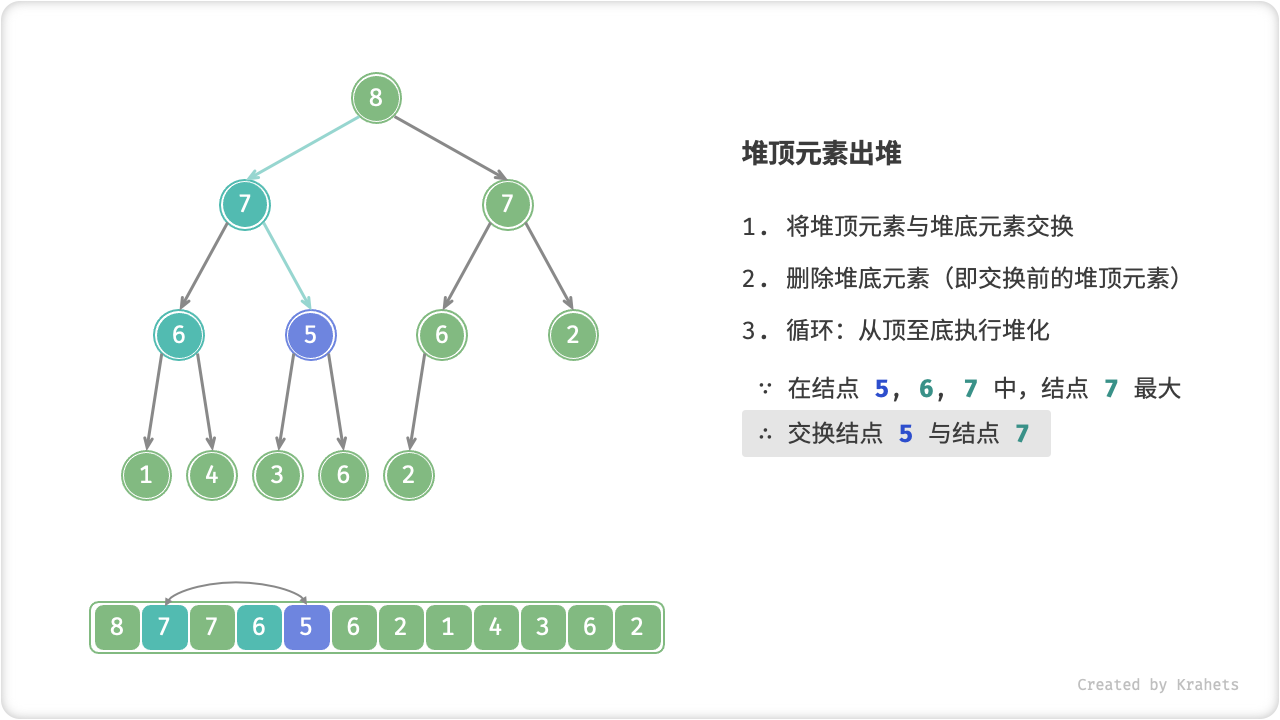
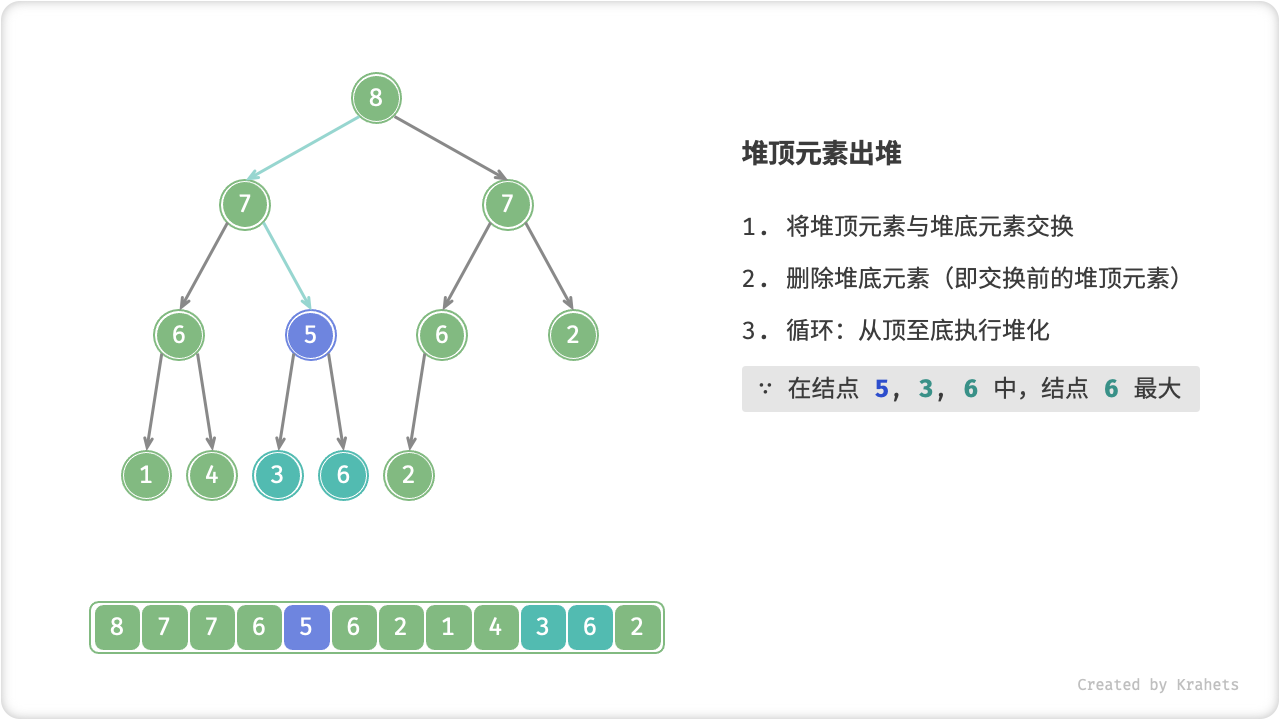
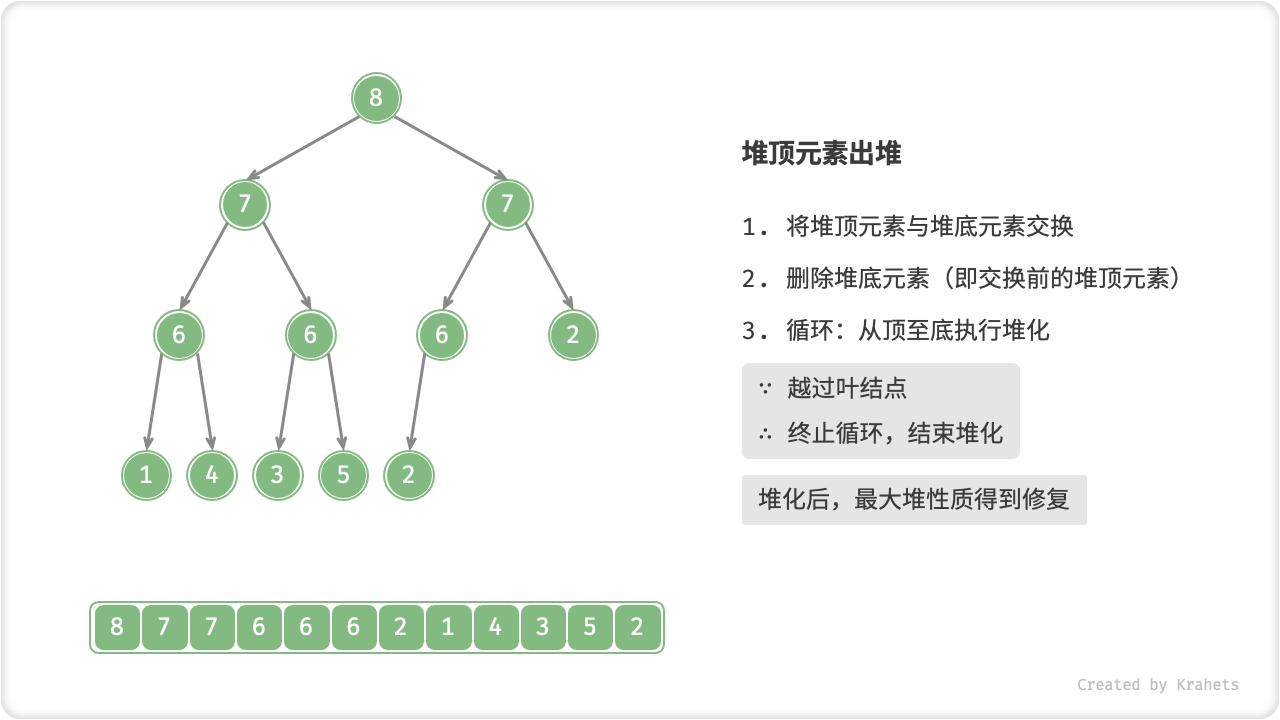
从根结点开始，从顶至底执行堆化；

顾名思义，从顶至底堆化的操作方向与从底至顶堆化相反，我们比较根结点的值与其两个子结点的值，将最大的子结点与根结点执行交换，并循环以上操作，直到越过叶结点时结束，或当遇到无需交换的结点时提前结束。

=== "Step 1"

=== "Step 2"

=== "Step 3"

=== "Step 4"

=== "Step 5"

=== "Step 6"

=== "Step 7"

=== "Step 8"

=== "Step 9"

=== "Step 10"

与元素入堆操作类似，堆顶元素出堆操作的时间复杂度为 O(\log n) 。

=== "Java"

```java title="my_heap.java"
[class]{MaxHeap}-[func]{poll}

[class]{MaxHeap}-[func]{siftDown}
```

=== "C++"

```cpp title="my_heap.cpp"
[class]{MaxHeap}-[func]{poll}

[class]{MaxHeap}-[func]{siftDown}
```

=== "Python"

```python title="my_heap.py"

```

=== "Go"

```go title="my_heap.go"
[class]{maxHeap}-[func]{poll}

[class]{maxHeap}-[func]{siftDown}
```

=== "JavaScript"

```javascript title="my_heap.js"
[class]{MaxHeap}-[func]{poll}

[class]{MaxHeap}-[func]{#siftDown}
```

=== "TypeScript"

```typescript title="my_heap.ts"
[class]{MaxHeap}-[func]{poll}

[class]{MaxHeap}-[func]{siftDown}
```

=== "C"

```c title="my_heap.c"
[class]{maxHeap}-[func]{poll}

[class]{maxHeap}-[func]{siftDown}
```

=== "C#"

```csharp title="my_heap.cs"
[class]{MaxHeap}-[func]{poll}

[class]{MaxHeap}-[func]{siftDown}
```

=== "Swift"

```swift title="my_heap.swift"
[class]{MaxHeap}-[func]{poll}

[class]{MaxHeap}-[func]{siftDown}
```

=== "Zig"

```zig title="my_heap.zig"
[class]{MaxHeap}-[func]{poll}

[class]{MaxHeap}-[func]{siftDown}
```

输入数据并建堆 *

如果我们想要直接输入一个列表并将其建堆，那么该怎么做呢？最直接地，考虑使用「元素入堆」方法，将列表元素依次入堆。元素入堆的时间复杂度为 O(\log n) ，而平均长度为 \frac{n}{2} ，因此该方法的总体时间复杂度为 O(n \log n) 。

然而，存在一种更加优雅的建堆方法。设结点数量为 n ，我们先将列表所有元素原封不动添加进堆，然后迭代地对各个结点执行「从顶至底堆化」。当然，无需对叶结点执行堆化，因为其没有子结点。

=== "Java"

```java title="my_heap.java"
[class]{MaxHeap}-[func]{MaxHeap}
```

=== "C++"

```cpp title="my_heap.cpp"
[class]{MaxHeap}-[func]{MaxHeap}
```

=== "Python"

```python title="my_heap.py"

```

=== "Go"

```go title="my_heap.go"
[class]{maxHeap}-[func]{newMaxHeap}
```

=== "JavaScript"

```javascript title="my_heap.js"
[class]{MaxHeap}-[func]{constructor}
```

=== "TypeScript"

```typescript title="my_heap.ts"
[class]{MaxHeap}-[func]{constructor}
```

=== "C"

```c title="my_heap.c"
[class]{maxHeap}-[func]{newMaxHeap}
```

=== "C#"

```csharp title="my_heap.cs"
[class]{MaxHeap}-[func]{MaxHeap}
```

=== "Swift"

```swift title="my_heap.swift"
[class]{MaxHeap}-[func]{init}
```

=== "Zig"

```zig title="my_heap.zig"
[class]{MaxHeap}-[func]{init}
```

那么，第二种建堆方法的时间复杂度时多少呢？我们来做一下简单推算。

完全二叉树中，设结点总数为 n ，则叶结点数量为 (n + 1) / 2 ，其中 / 为向下整除。因此在排除叶结点后，需要堆化结点数量为 (n - 1)/2 ，即为 O(n) ；
从顶至底堆化中，每个结点最多堆化至叶结点，因此最大迭代次数为二叉树高度 O(\log n) ；

将上述两者相乘，可得时间复杂度为 O(n \log n) 。然而，该估算结果仍不够准确，因为我们没有考虑到 二叉树底层结点远多于顶层结点 的性质。

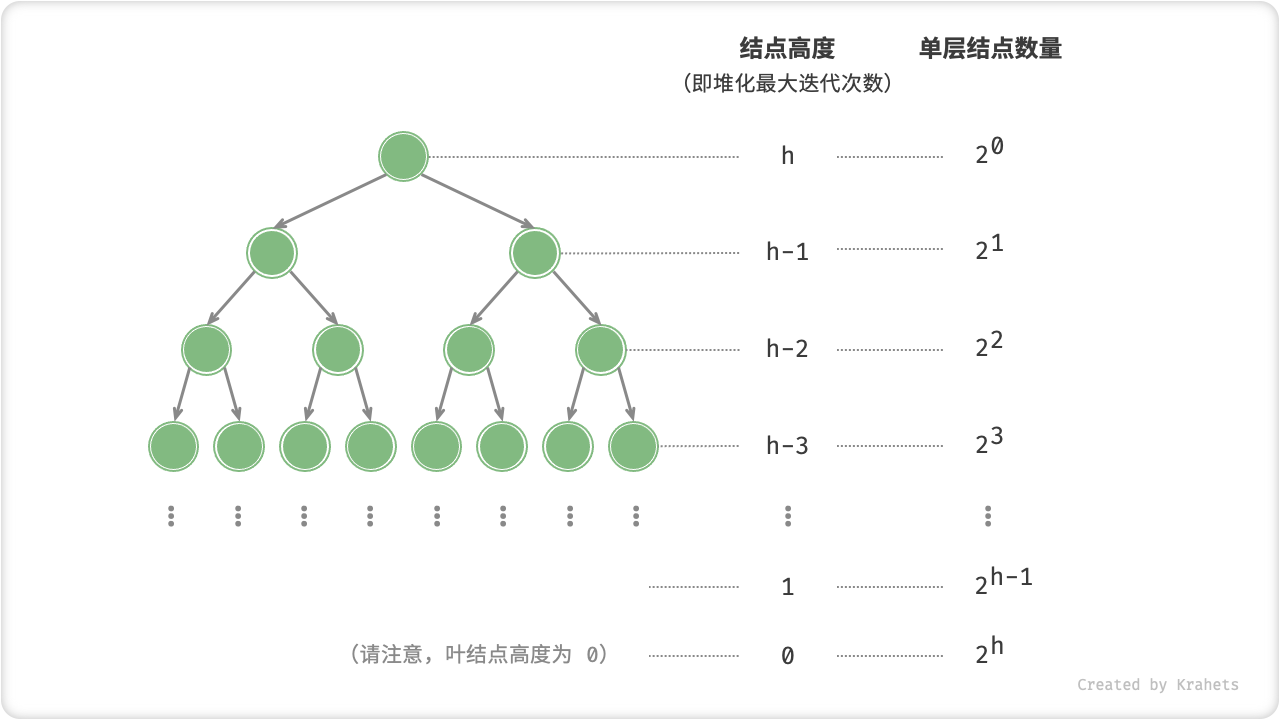
下面我们来尝试展开计算。为了减小计算难度，我们假设树是一个「完美二叉树」，该假设不会影响计算结果的正确性。设二叉树（即堆）结点数量为 n ，树高度为 h 。上文提到，结点堆化最大迭代次数等于该结点到叶结点的距离，而这正是“结点高度”。因此，我们将各层的“结点数量 \times 结点高度”求和，即可得到所有结点的堆化的迭代次数总和。


T(h) = 2^0h + 2^1(h-1) + 2^2(h-2) + \cdots + 2^{(h-1)}\times1

化简上式需要借助中学的数列知识，先对 T(h) 乘以 2 ，易得


\begin{aligned}
T(h) & = 2^0h + 2^1(h-1) + 2^2(h-2) + \cdots + 2^{h-1}\times1 \newline
2 T(h) & = 2^1h + 2^2(h-1) + 2^3(h-2) + \cdots + 2^{h}\times1 \newline
\end{aligned}

使用错位相减法，令下式 2 T(h) 减去上式 T(h) ，可得


2T(h) - T(h) = T(h) = -2^0h + 2^1 + 2^2 + \cdots + 2^{h-1} + 2^h

观察上式，T(h) 是一个等比数列，可直接使用求和公式，得到时间复杂度为


\begin{aligned}
T(h) & = 2 \frac{1 - 2^h}{1 - 2} - h \newline
& = 2^{h+1} - h \newline
& = O(2^h)
\end{aligned}

进一步地，高度为 h 的完美二叉树的结点数量为 n = 2^{h+1} - 1 ，易得复杂度为 O(2^h) = O(n)。以上推算表明，输入列表并建堆的时间复杂度为 O(n) ，非常高效。

堆常见应用

优先队列。堆常作为实现优先队列的首选数据结构，入队和出队操作时间复杂度为 O(\log n) ，建队操作为 O(n) ，皆非常高效。
堆排序。给定一组数据，我们使用其建堆，并依次全部弹出，则可以得到有序的序列。当然，堆排序一般无需弹出元素，仅需每轮将堆顶元素交换至数组尾部并减小堆的长度即可。
获取最大的 k 个元素。这既是一道经典算法题目，也是一种常见应用，例如选取热度前 10 的新闻作为微博热搜，选取前 10 销量的商品等。

20 KiB Raw Blame History Unescape Escape

堆

堆术语与性质

堆常用操作

堆的实现

堆的存储与表示

访问堆顶元素

元素入堆

堆顶元素出堆

输入数据并建堆 *

堆常见应用

20 KiB

Raw Blame History Unescape Escape