You can not select more than 25 topics
Topics must start with a letter or number, can include dashes ('-') and can be up to 35 characters long.
6.7 KiB
6.7 KiB
| comments |
|---|
| true |
9.2. 图基础操作
图的基础操作分为对「边」的操作和对「顶点」的操作,在「邻接矩阵」和「邻接表」这两种表示下的实现方式不同。
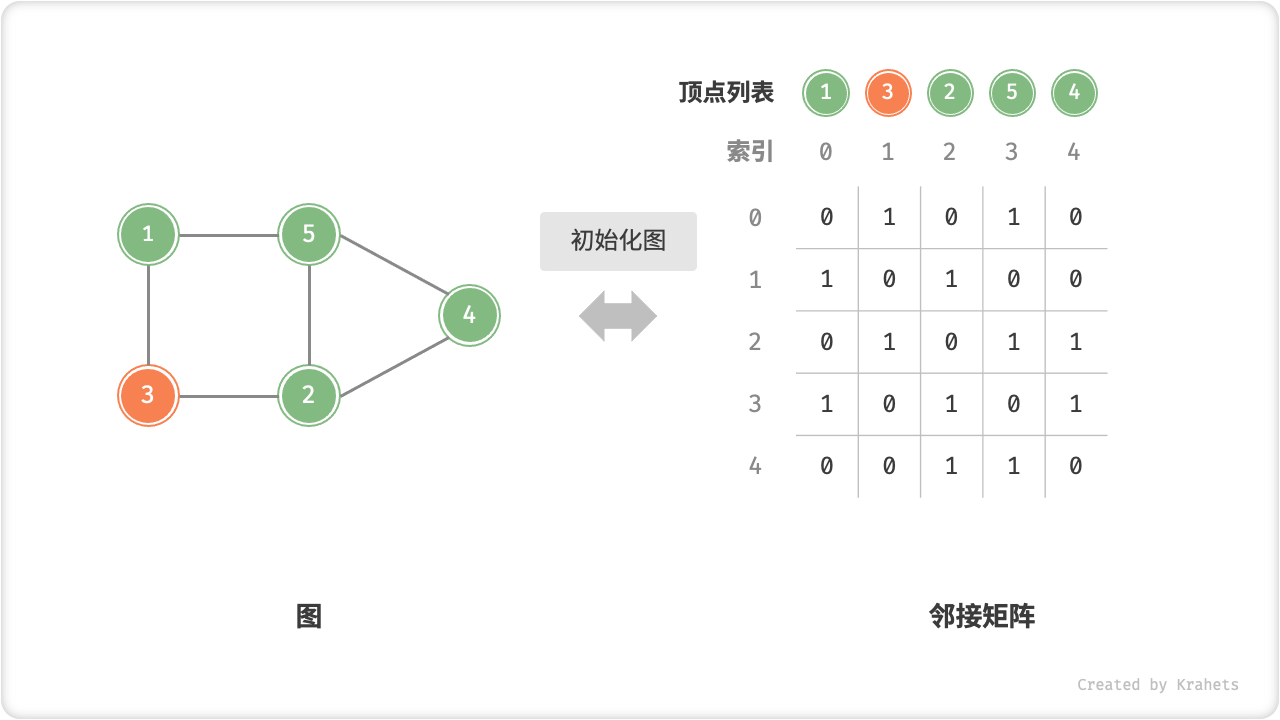
9.2.1. 基于邻接矩阵的实现
设图的顶点总数为 n ,则有:
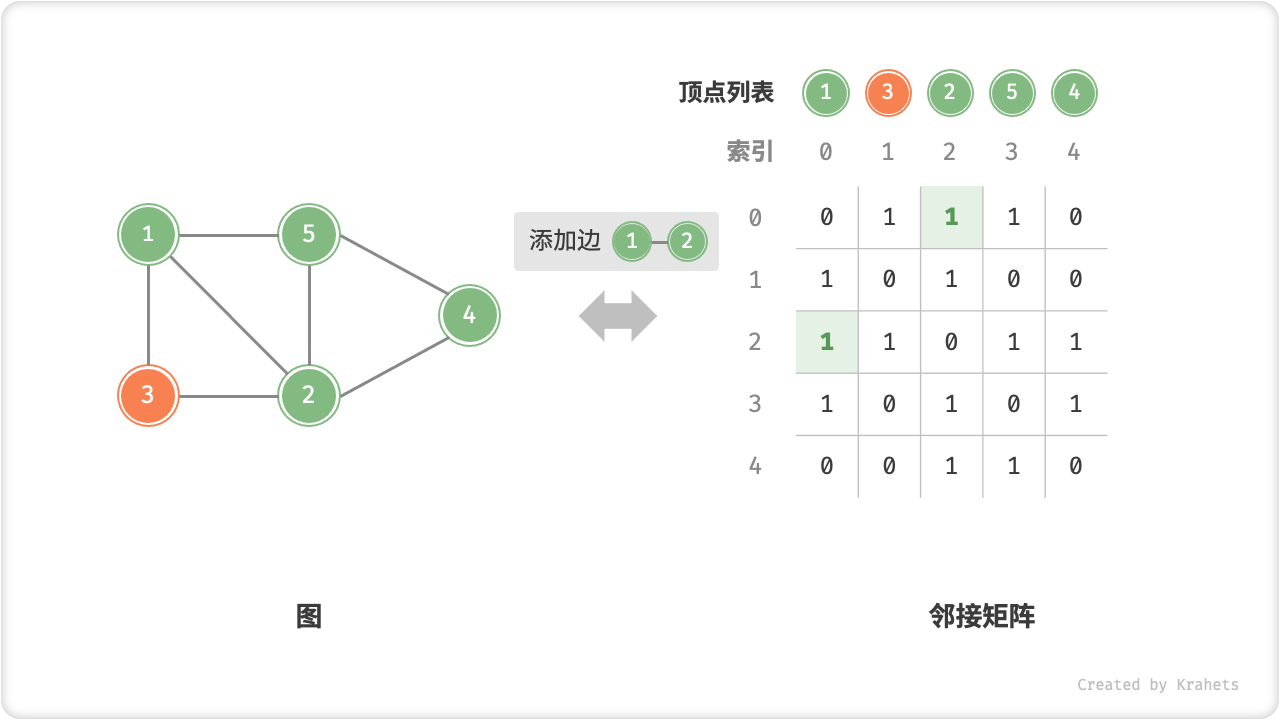
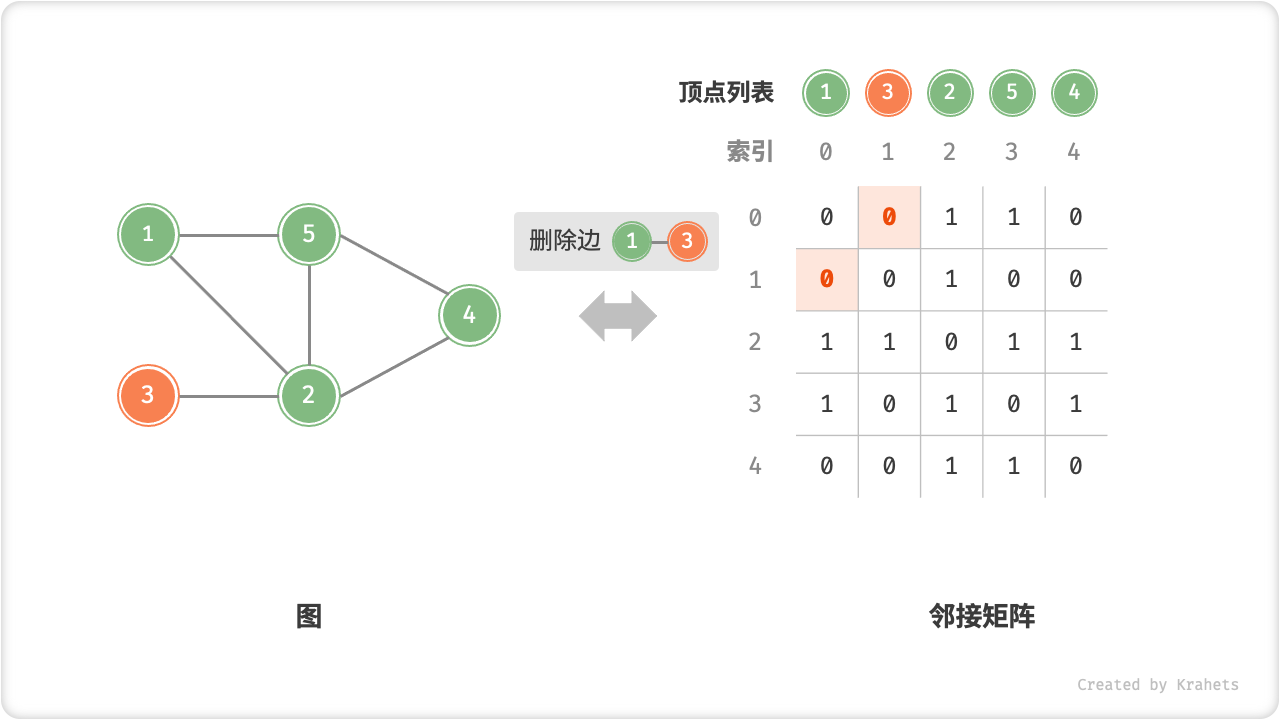
- 添加或删除边:直接在邻接矩阵中修改指定边的对应元素即可,使用
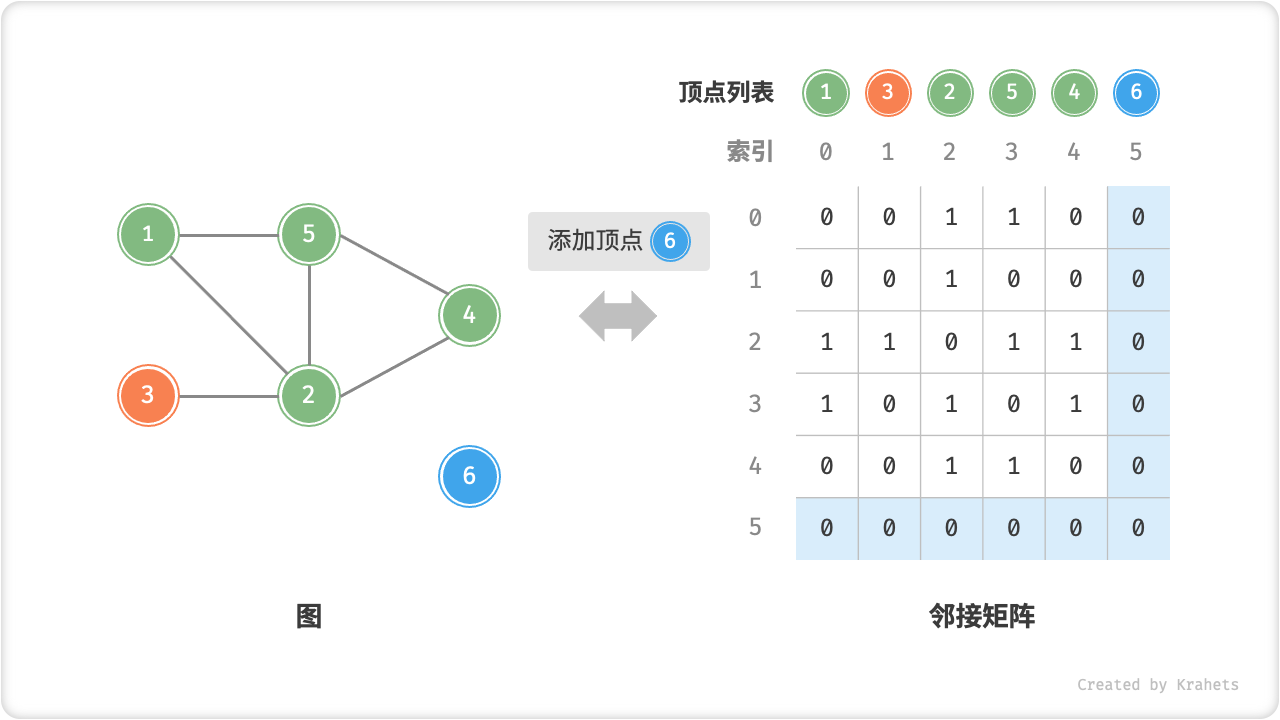
O(1)时间。而由于是无向图,因此需要同时更新两个方向的边。 - 添加顶点:在邻接矩阵的尾部添加一行一列,并全部填
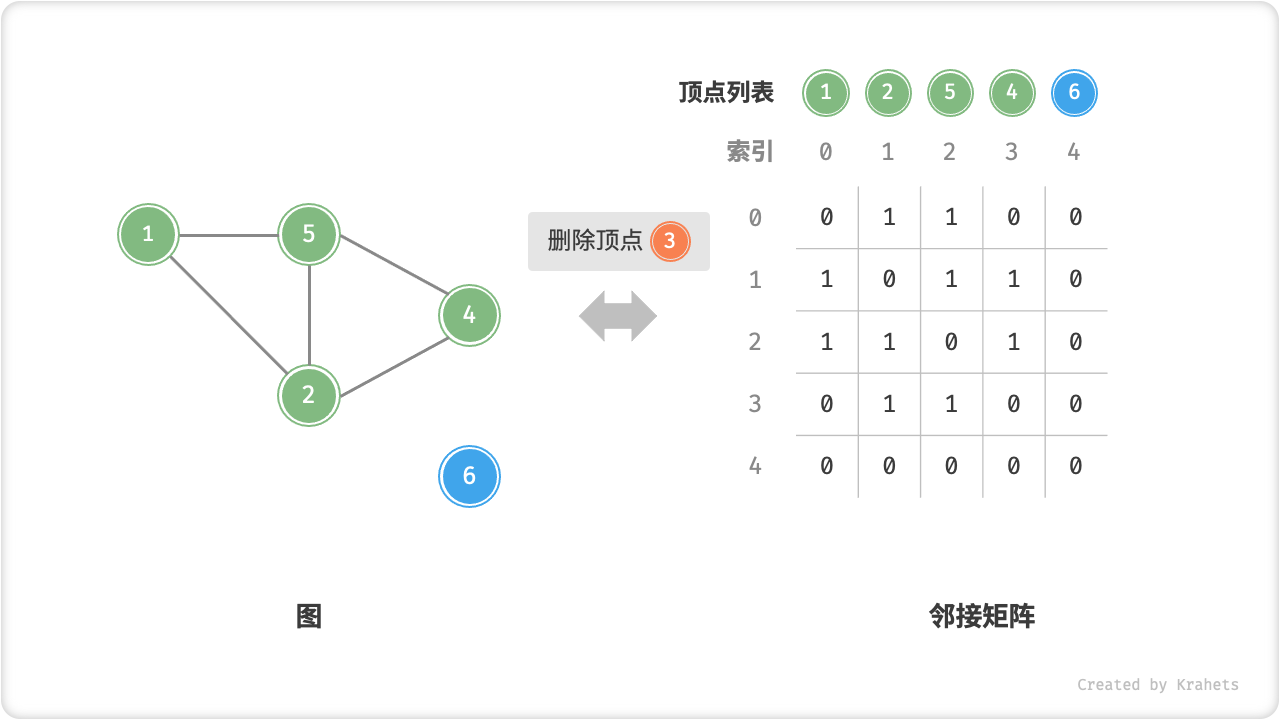
0即可,使用O(n)时间。 - 删除顶点:在邻接矩阵中删除一行一列。当删除首行首列时达到最差情况,需要将
(n-1)^2个元素“向左上移动”,从而使用O(n^2)时间。 - 初始化:传入
n个顶点,初始化长度为n的顶点列表vertices,使用O(n)时间;初始化n \times n大小的邻接矩阵adjMat,使用O(n^2)时间。
以下是基于邻接矩阵表示图的实现代码。
=== "Java"
```java title="graph_adjacency_matrix.java"
[class]{GraphAdjMat}-[func]{}
```
=== "C++"
```cpp title="graph_adjacency_matrix.cpp"
[class]{GraphAdjMat}-[func]{}
```
=== "Python"
```python title="graph_adjacency_matrix.py"
[class]{GraphAdjMat}-[func]{}
```
=== "Go"
```go title="graph_adjacency_matrix.go"
[class]{graphAdjMat}-[func]{}
```
=== "JavaScript"
```javascript title="graph_adjacency_matrix.js"
[class]{GraphAdjMat}-[func]{}
```
=== "TypeScript"
```typescript title="graph_adjacency_matrix.ts"
[class]{GraphAdjMat}-[func]{}
```
=== "C"
```c title="graph_adjacency_matrix.c"
[class]{graphAdjMat}-[func]{}
```
=== "C#"
```csharp title="graph_adjacency_matrix.cs"
[class]{GraphAdjMat}-[func]{}
```
=== "Swift"
```swift title="graph_adjacency_matrix.swift"
[class]{GraphAdjMat}-[func]{}
```
=== "Zig"
```zig title="graph_adjacency_matrix.zig"
```
9.2.2. 基于邻接表的实现
设图的顶点总数为 n 、边总数为 m ,则有:
- 添加边:在顶点对应链表的尾部添加边即可,使用
O(1)时间。因为是无向图,所以需要同时添加两个方向的边。 - 删除边:在顶点对应链表中查询与删除指定边,使用
O(m)时间。与添加边一样,需要同时删除两个方向的边。 - 添加顶点:在邻接表中添加一个链表即可,并以新增顶点为链表头结点,使用
O(1)时间。 - 删除顶点:需要遍历整个邻接表,删除包含指定顶点的所有边,使用
O(n + m)时间。 - 初始化:需要在邻接表中建立
n个结点和2m条边,使用O(n + m)时间。
基于邻接表实现图的代码如下所示。
!!! question "为什么需要使用顶点类 Vertex ?"
如果我们直接通过顶点值来区分不同顶点,那么值重复的顶点将无法被区分。
如果建立一个顶点列表,用索引来区分不同顶点,那么假设我们想要删除索引为 `i` 的顶点,则需要遍历整个邻接表,将其中 $> i$ 的索引全部执行 $-1$ ,这样的操作是比较耗时的。
因此,通过引入顶点类 `Vertex` ,每个顶点都是唯一的对象,这样在删除操作时就无需改动其余顶点了。
=== "Java"
```java title="graph_adjacency_list.java"
[class]{Vertex}-[func]{}
[class]{GraphAdjList}-[func]{}
```
=== "C++"
```cpp title="graph_adjacency_list.cpp"
[class]{Vertex}-[func]{}
[class]{GraphAdjList}-[func]{}
```
=== "Python"
```python title="graph_adjacency_list.py"
[class]{Vertex}-[func]{}
[class]{GraphAdjList}-[func]{}
```
=== "Go"
```go title="graph_adjacency_list.go"
[class]{vertex}-[func]{}
[class]{graphAdjList}-[func]{}
```
=== "JavaScript"
```javascript title="graph_adjacency_list.js"
[class]{Vertex}-[func]{}
[class]{GraphAdjList}-[func]{}
```
=== "TypeScript"
```typescript title="graph_adjacency_list.ts"
[class]{Vertex}-[func]{}
[class]{GraphAdjList}-[func]{}
```
=== "C"
```c title="graph_adjacency_list.c"
[class]{vertex}-[func]{}
[class]{graphAdjList}-[func]{}
```
=== "C#"
```csharp title="graph_adjacency_list.cs"
[class]{Vertex}-[func]{}
[class]{GraphAdjList}-[func]{}
```
=== "Swift"
```swift title="graph_adjacency_list.swift"
[class]{Vertex}-[func]{}
[class]{GraphAdjList}-[func]{}
```
=== "Zig"
```zig title="graph_adjacency_list.zig"
[class]{Vertex}-[func]{}
[class]{GraphAdjList}-[func]{}
```
9.2.3. 效率对比
设图中共有 n 个顶点和 m 条边,下表为邻接矩阵和邻接表的时间和空间效率对比。
| 邻接矩阵 | 邻接表(链表) | 邻接表(哈希表) | |
|---|---|---|---|
| 判断是否邻接 | O(1) |
O(m) |
O(1) |
| 添加边 | O(1) |
O(1) |
O(1) |
| 删除边 | O(1) |
O(m) |
O(1) |
| 添加顶点 | O(n) |
O(1) |
O(1) |
| 删除顶点 | O(n^2) |
O(n + m) |
O(n) |
| 内存空间占用 | O(n^2) |
O(n + m) |
O(n + m) |
观察上表,貌似邻接表(哈希表)的时间与空间效率最优。但实际上,在邻接矩阵中操作边的效率更高,只需要一次数组访问或赋值操作即可。总结以上,邻接矩阵体现“以空间换时间”,邻接表体现“以时间换空间”。