6.3 KiB
圖的走訪
樹代表的是“一對多”的關係,而圖則具有更高的自由度,可以表示任意的“多對多”關係。因此,我們可以把樹看作圖的一種特例。顯然,樹的走訪操作也是圖的走訪操作的一種特例。
圖和樹都需要應用搜索演算法來實現走訪操作。圖的走訪方式也可分為兩種:廣度優先走訪和深度優先走訪。
廣度優先走訪
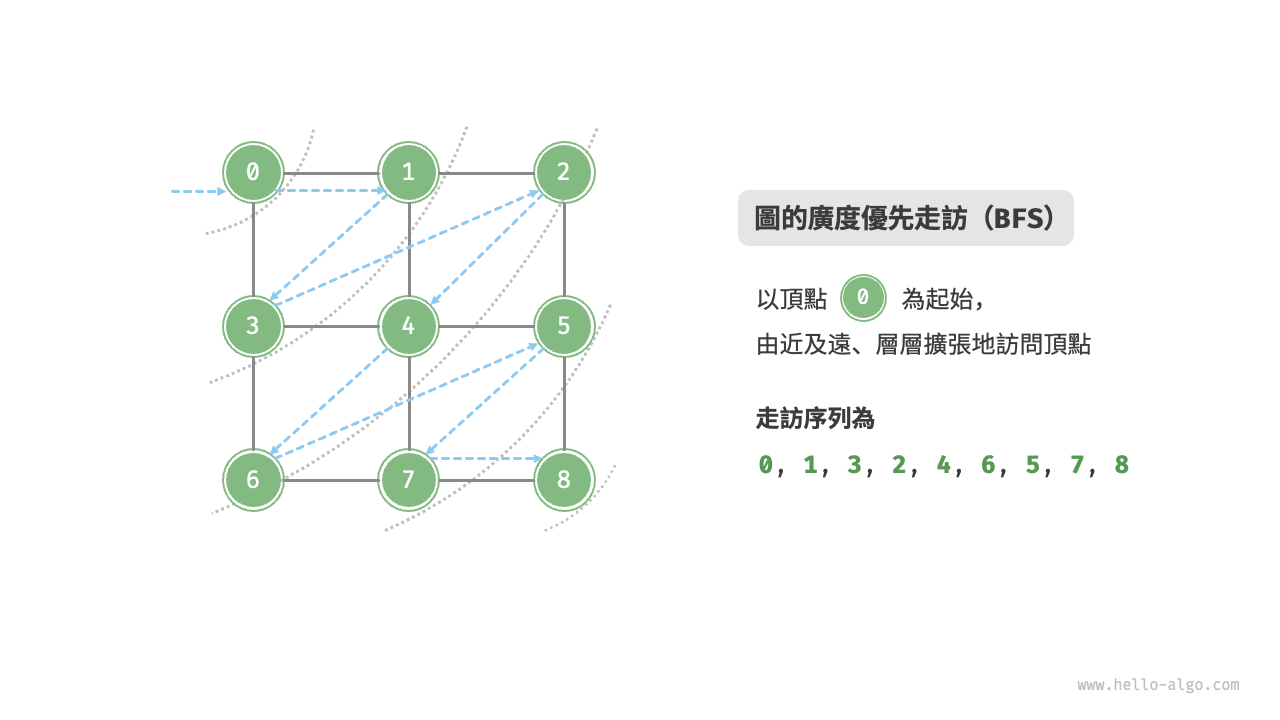
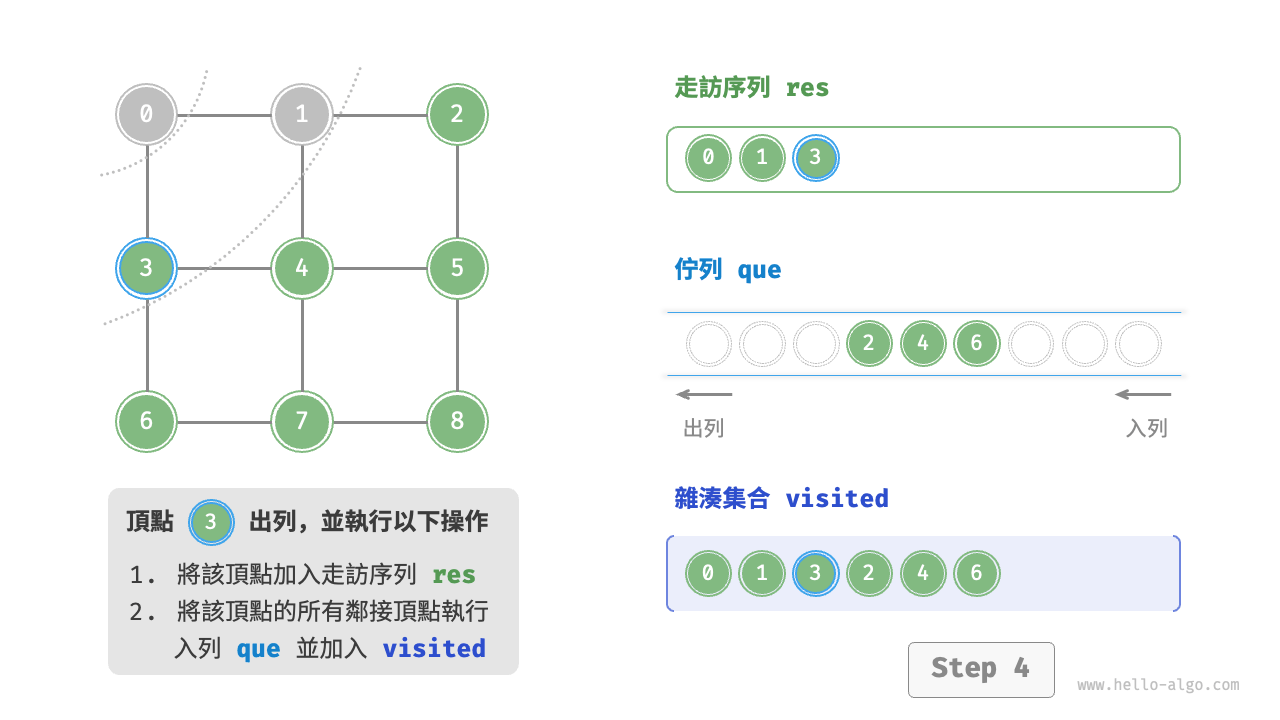
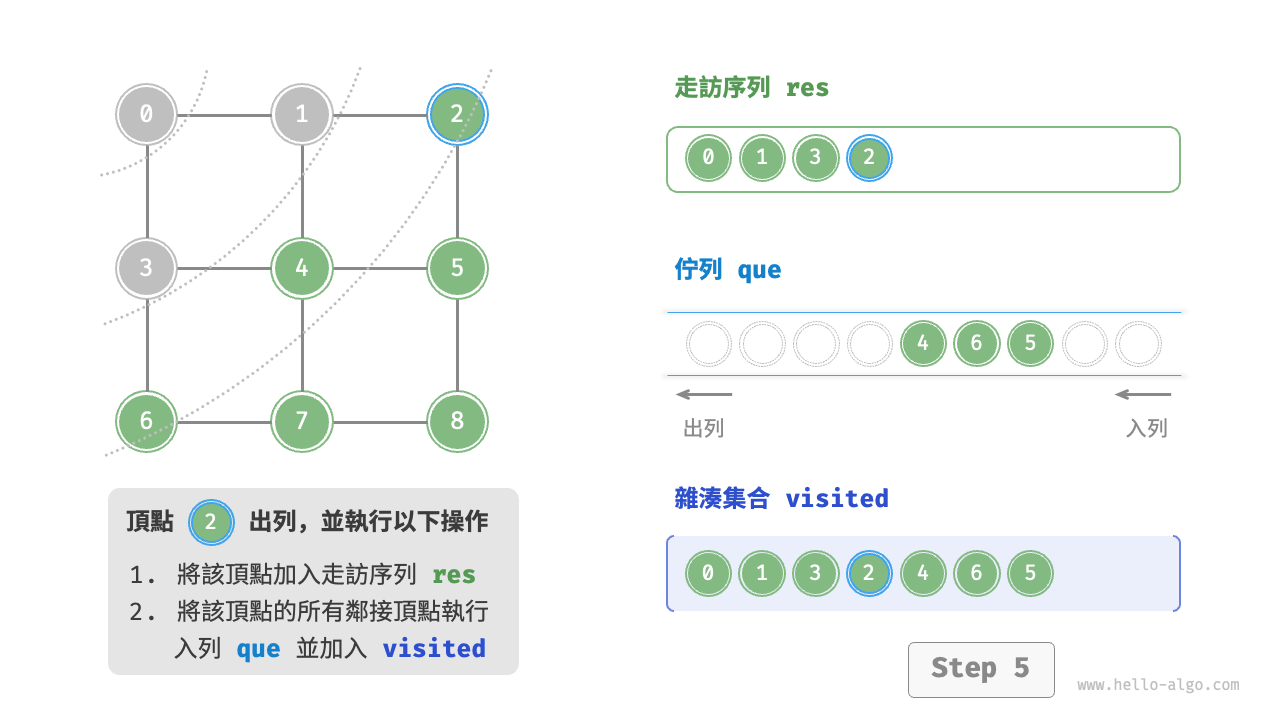
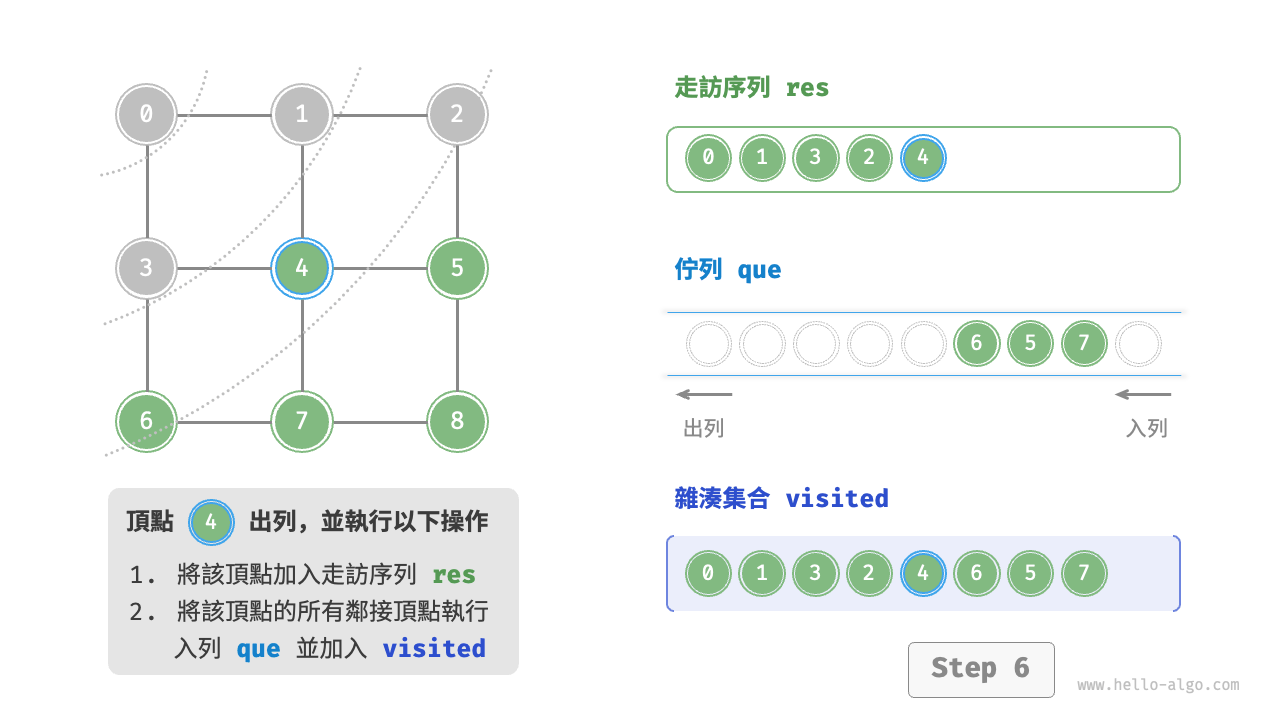
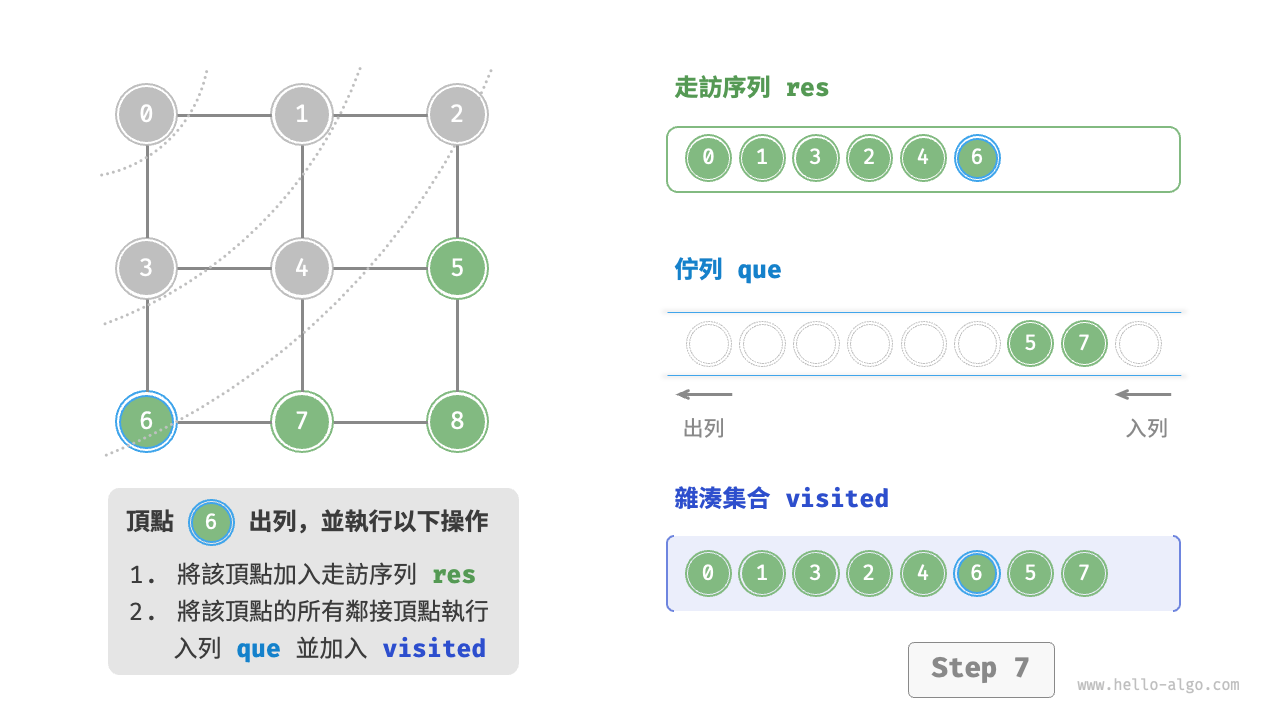
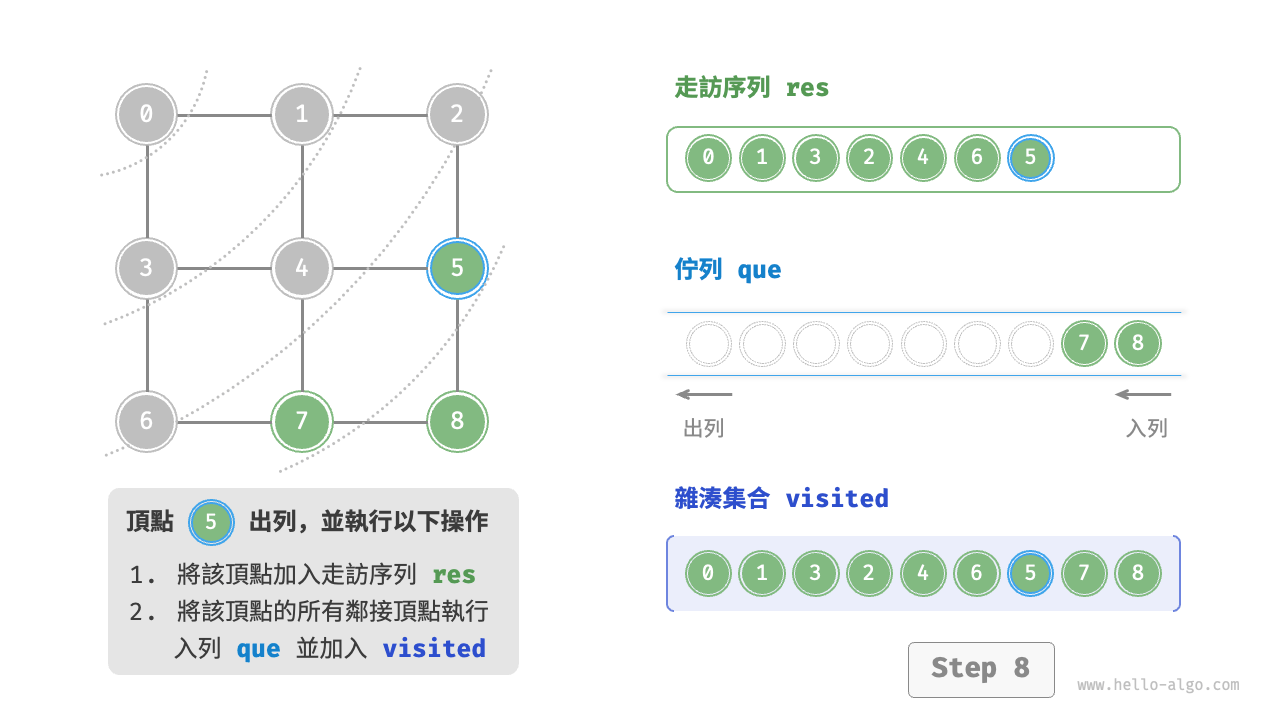
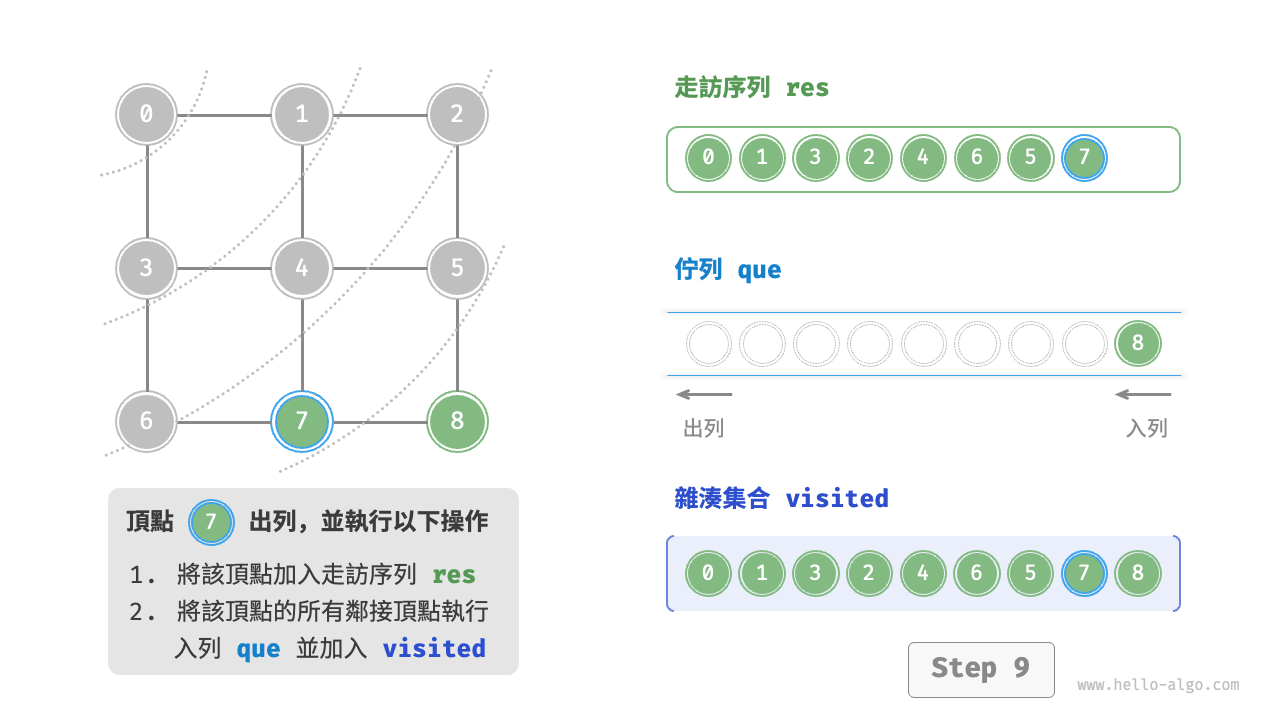
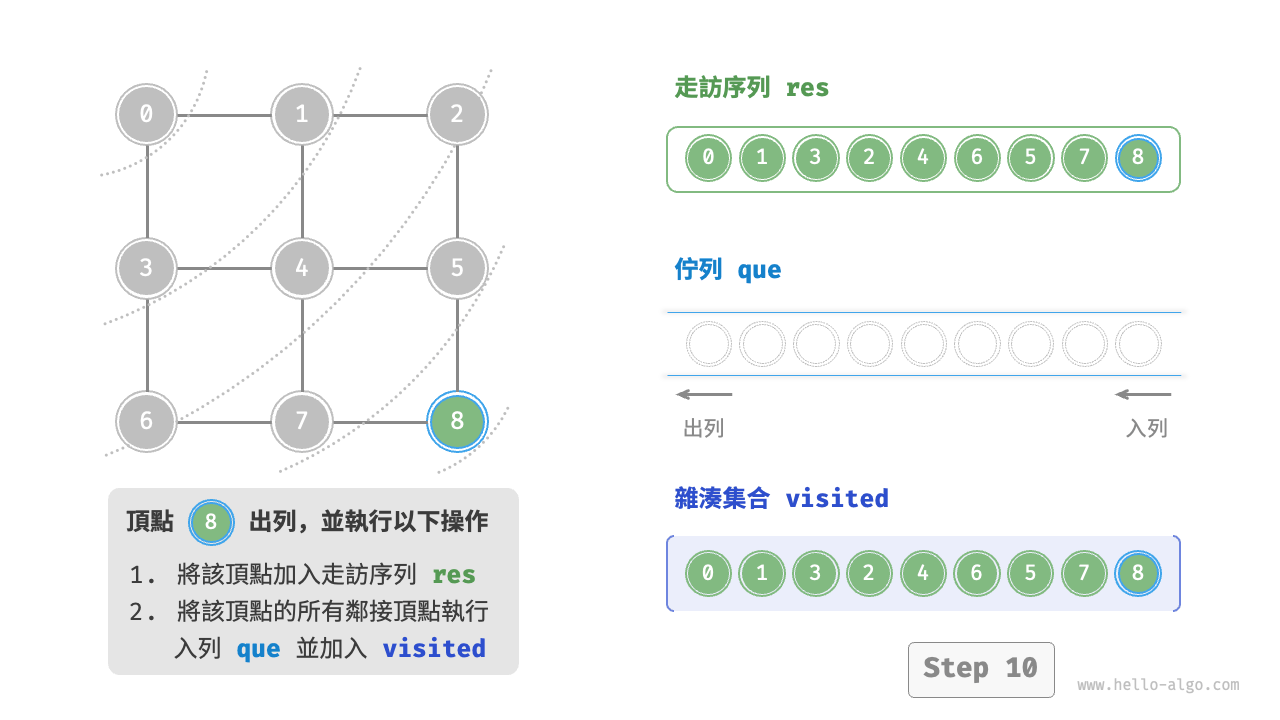
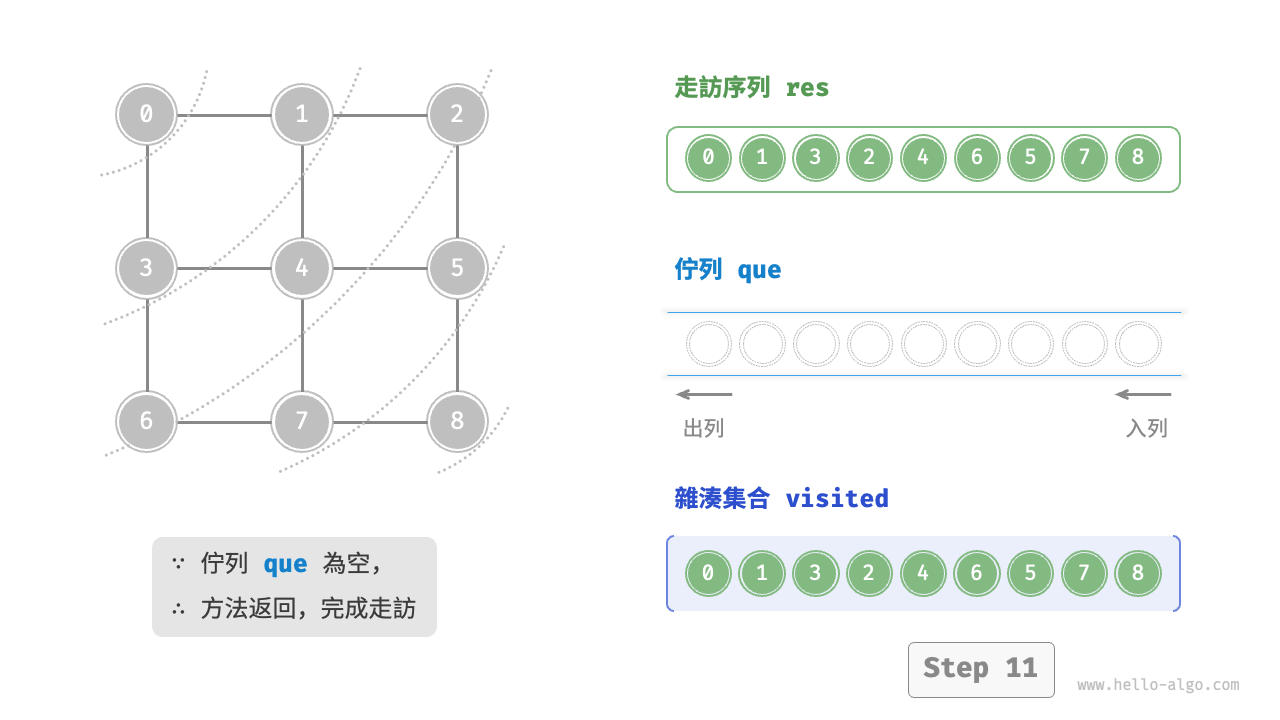
廣度優先走訪是一種由近及遠的走訪方式,從某個節點出發,始終優先訪問距離最近的頂點,並一層層向外擴張。如下圖所示,從左上角頂點出發,首先走訪該頂點的所有鄰接頂點,然後走訪下一個頂點的所有鄰接頂點,以此類推,直至所有頂點訪問完畢。
演算法實現
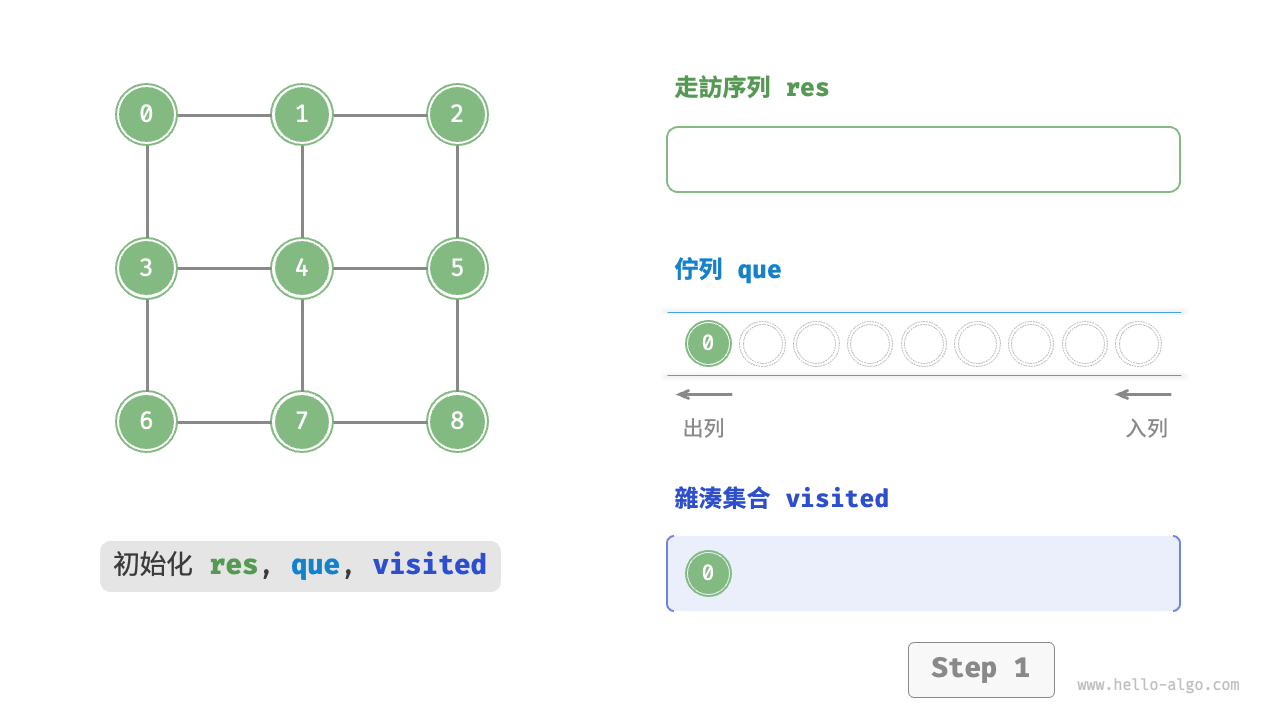
BFS 通常藉助佇列來實現,程式碼如下所示。佇列具有“先入先出”的性質,這與 BFS 的“由近及遠”的思想異曲同工。
- 將走訪起始頂點
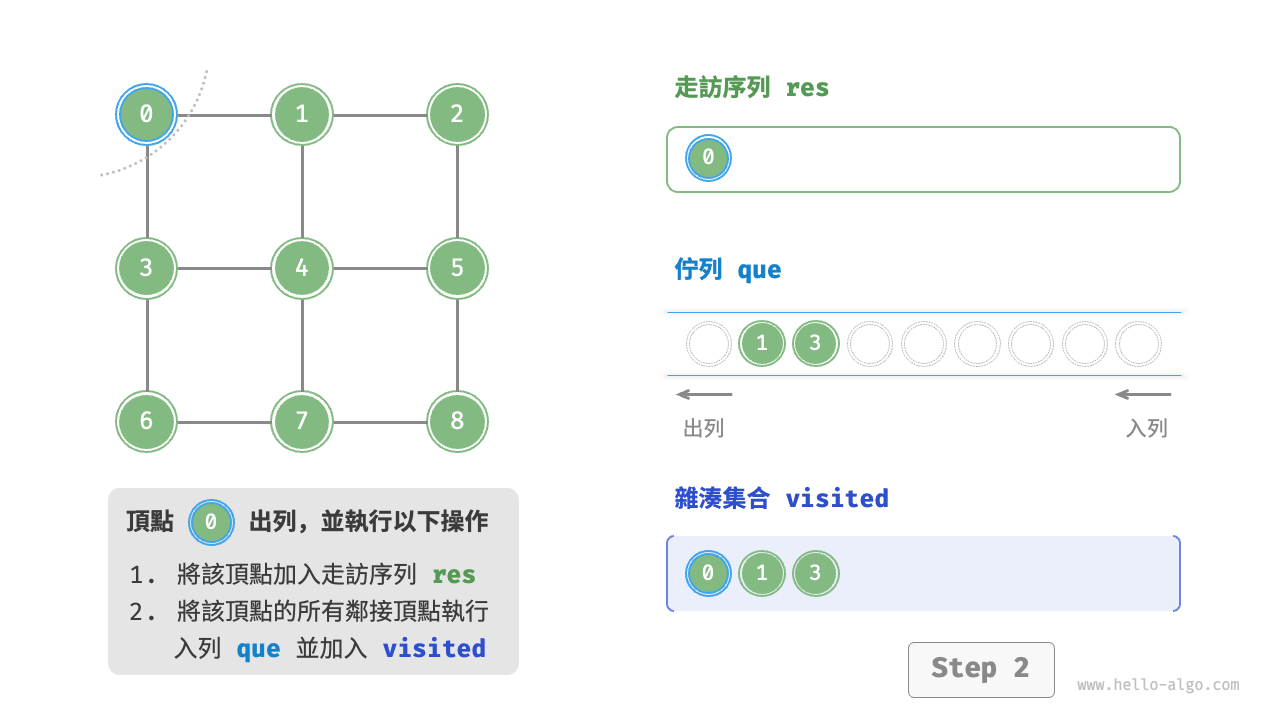
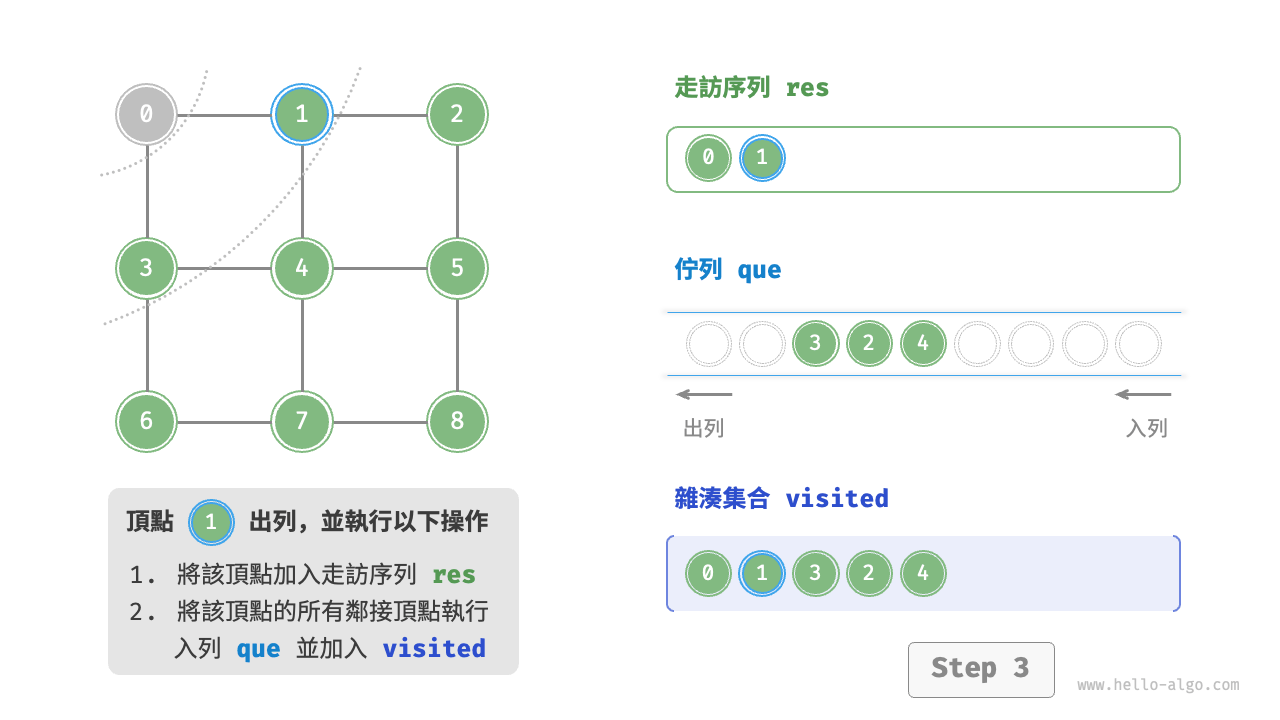
startVet加入列列,並開啟迴圈。 - 在迴圈的每輪迭代中,彈出佇列首頂點並記錄訪問,然後將該頂點的所有鄰接頂點加入到佇列尾部。
- 迴圈步驟
2.,直到所有頂點被訪問完畢後結束。
為了防止重複走訪頂點,我們需要藉助一個雜湊集合 visited 來記錄哪些節點已被訪問。
!!! tip
雜湊集合可以看作一個只儲存 `key` 而不儲存 `value` 的雜湊表,它可以在 $O(1)$ 時間複雜度下進行 `key` 的增刪查改操作。根據 `key` 的唯一性,雜湊集合通常用於資料去重等場景。
[file]{graph_bfs}-[class]{}-[func]{graph_bfs}
程式碼相對抽象,建議對照下圖來加深理解。
!!! question "廣度優先走訪的序列是否唯一?"
不唯一。廣度優先走訪只要求按“由近及遠”的順序走訪,**而多個相同距離的頂點的走訪順序允許被任意打亂**。以上圖為例,頂點 $1$、$3$ 的訪問順序可以交換,頂點 $2$、$4$、$6$ 的訪問順序也可以任意交換。
複雜度分析
時間複雜度:所有頂點都會入列並出隊一次,使用 O(|V|) 時間;在走訪鄰接頂點的過程中,由於是無向圖,因此所有邊都會被訪問 2 次,使用 O(2|E|) 時間;總體使用 O(|V| + |E|) 時間。
空間複雜度:串列 res ,雜湊集合 visited ,佇列 que 中的頂點數量最多為 |V| ,使用 O(|V|) 空間。
深度優先走訪
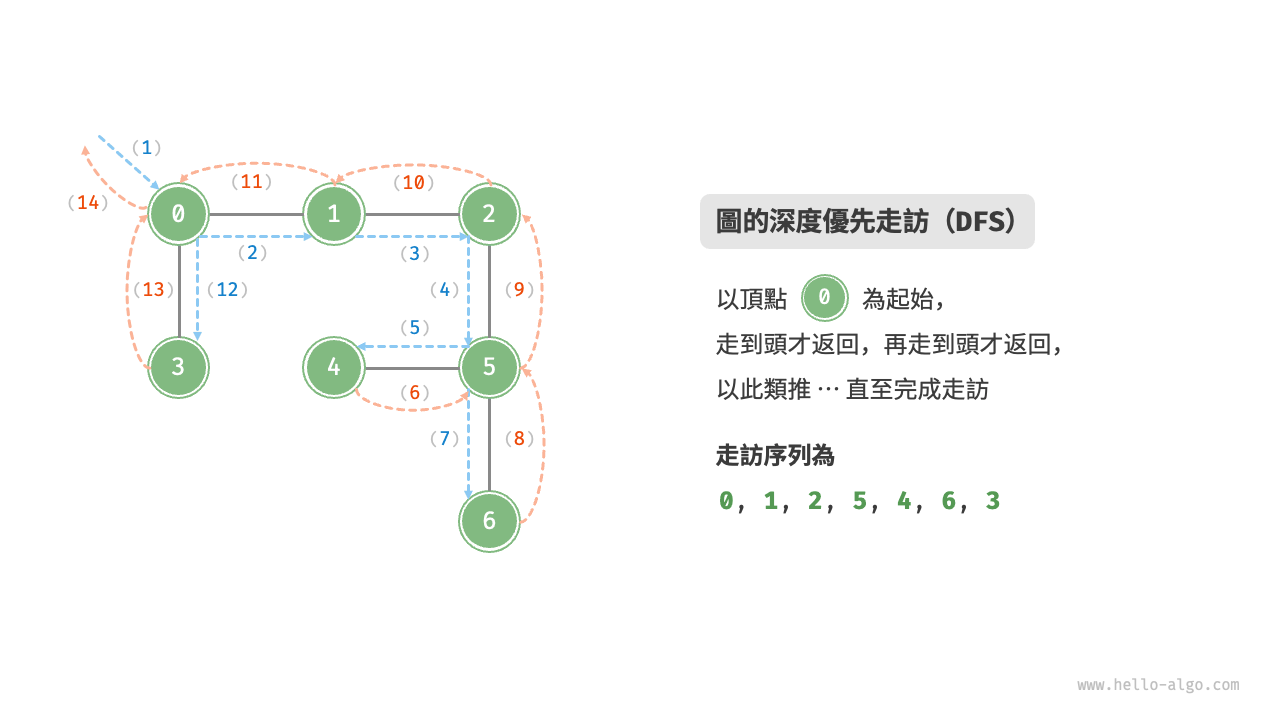
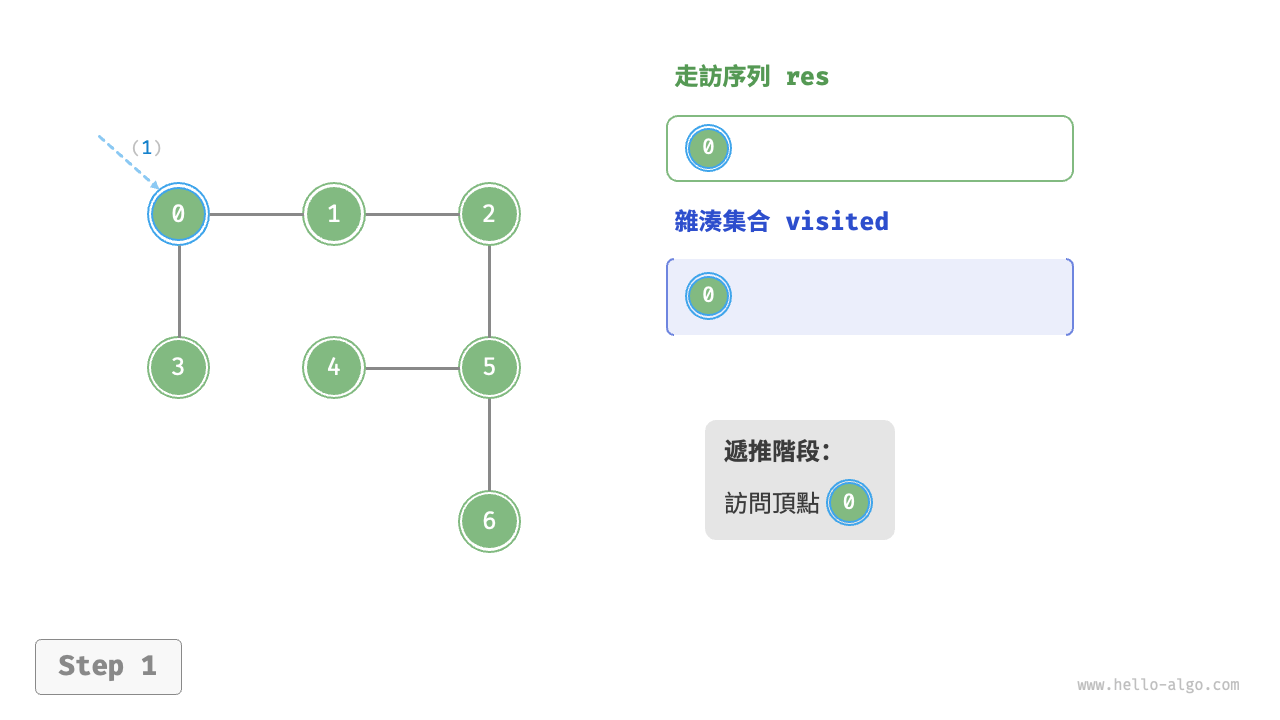
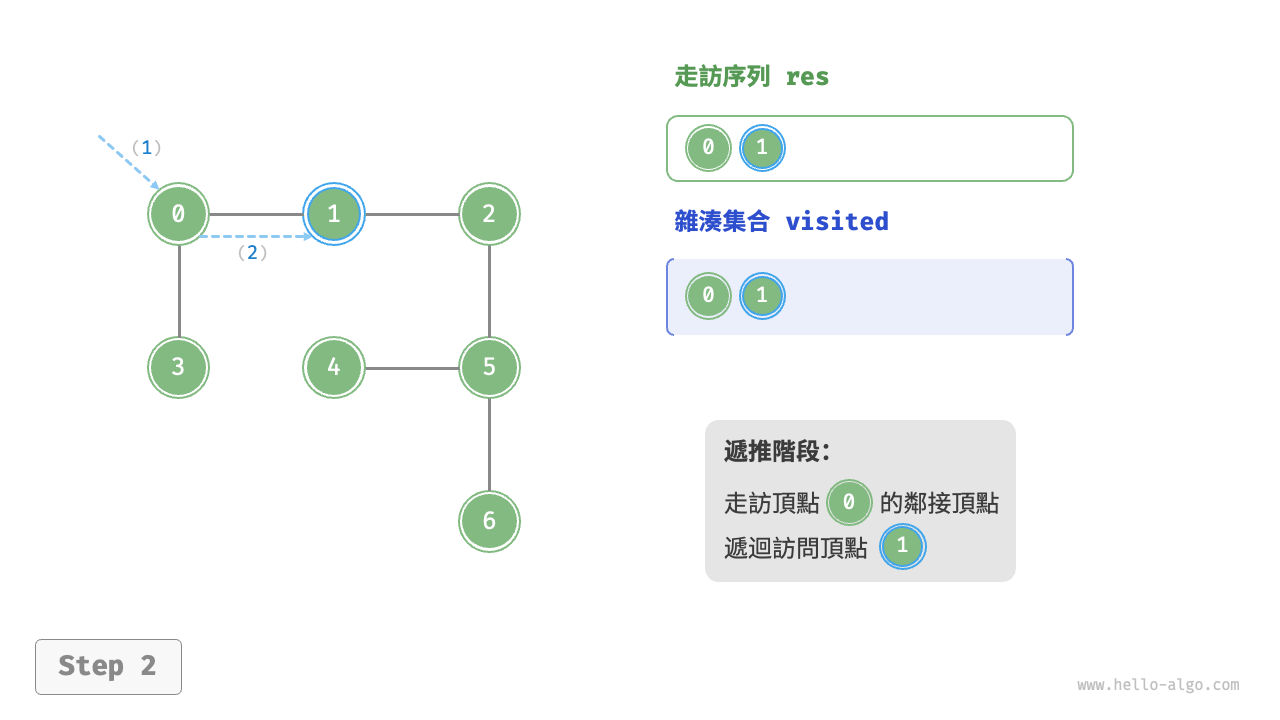
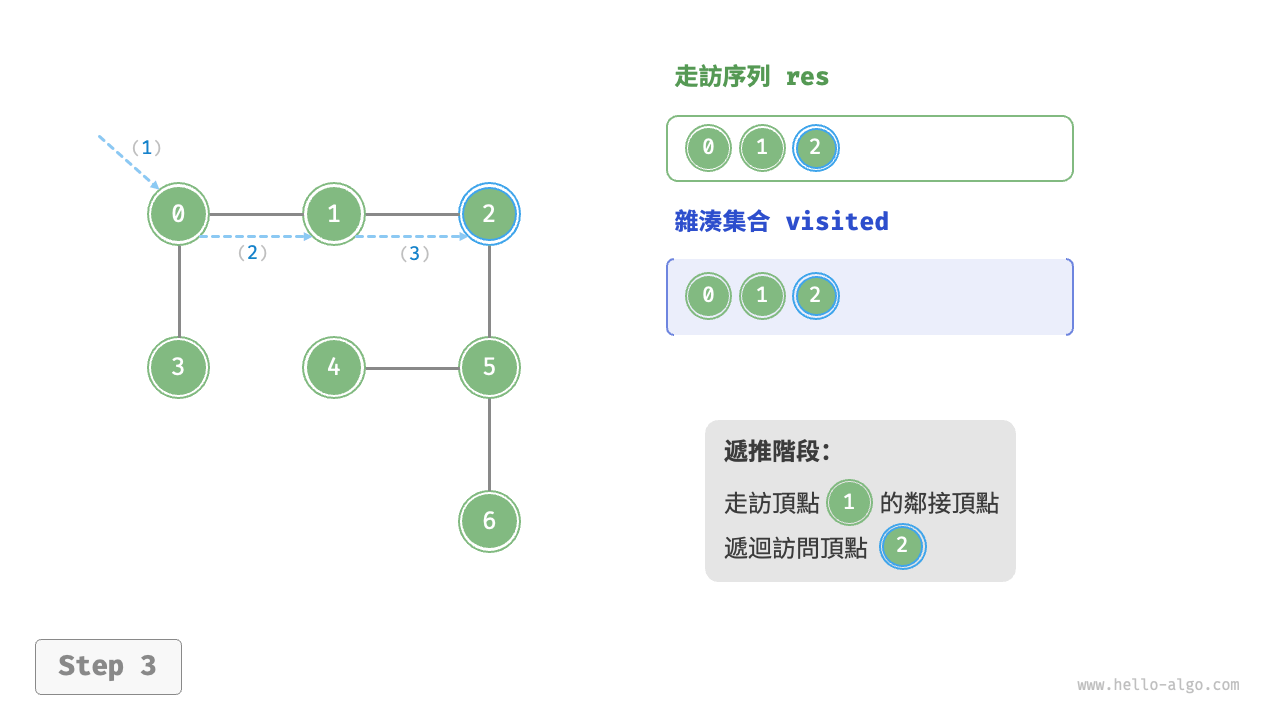
深度優先走訪是一種優先走到底、無路可走再回頭的走訪方式。如下圖所示,從左上角頂點出發,訪問當前頂點的某個鄰接頂點,直到走到盡頭時返回,再繼續走到盡頭並返回,以此類推,直至所有頂點走訪完成。
演算法實現
這種“走到盡頭再返回”的演算法範式通常基於遞迴來實現。與廣度優先走訪類似,在深度優先走訪中,我們也需要藉助一個雜湊集合 visited 來記錄已被訪問的頂點,以避免重複訪問頂點。
[file]{graph_dfs}-[class]{}-[func]{graph_dfs}
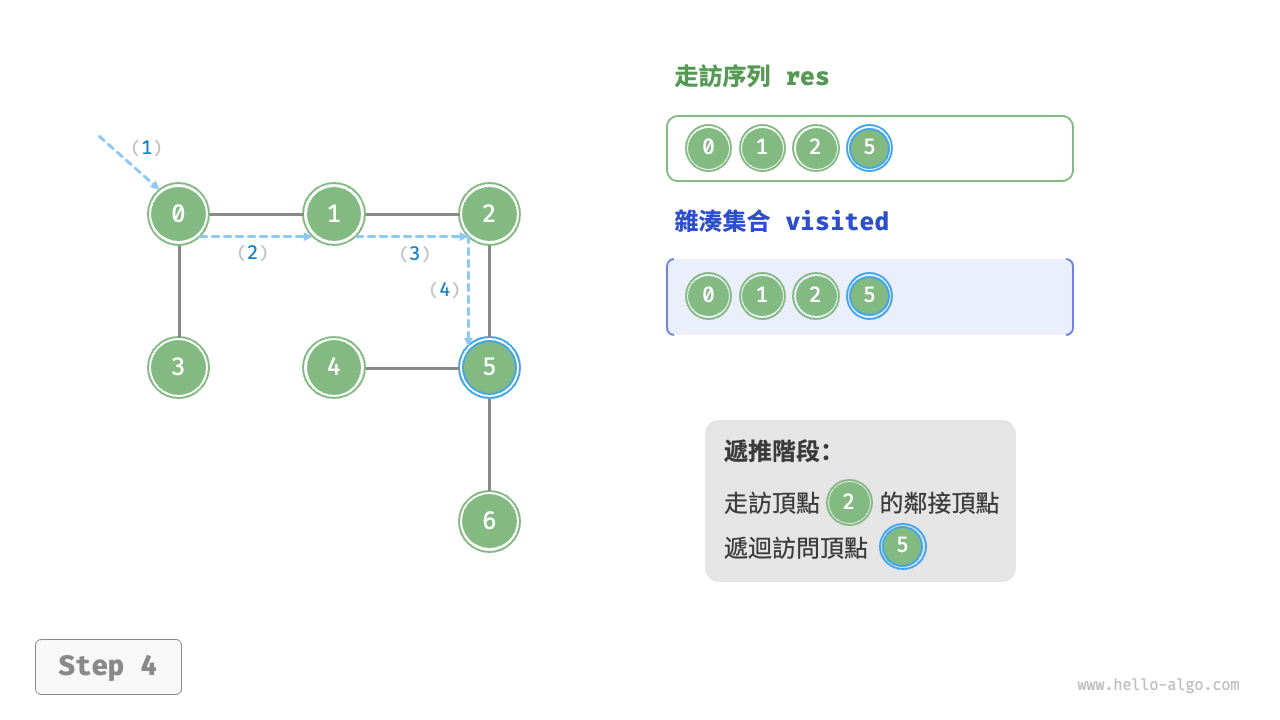
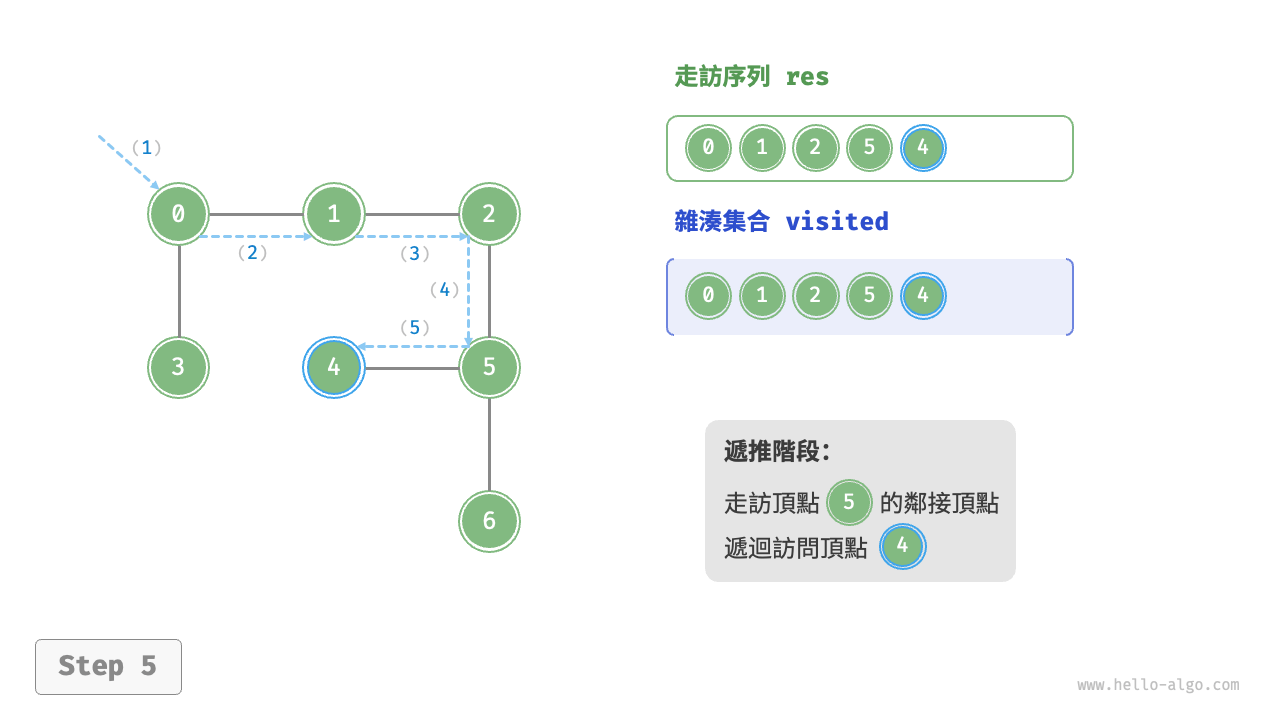
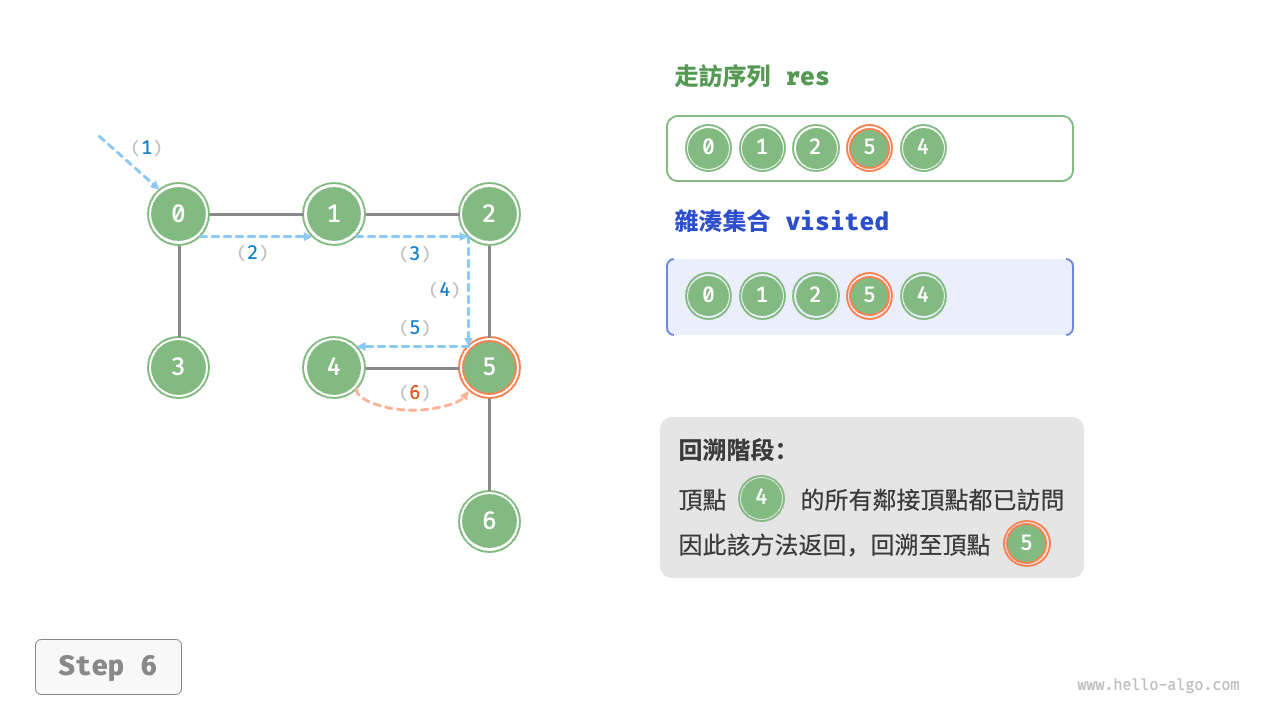
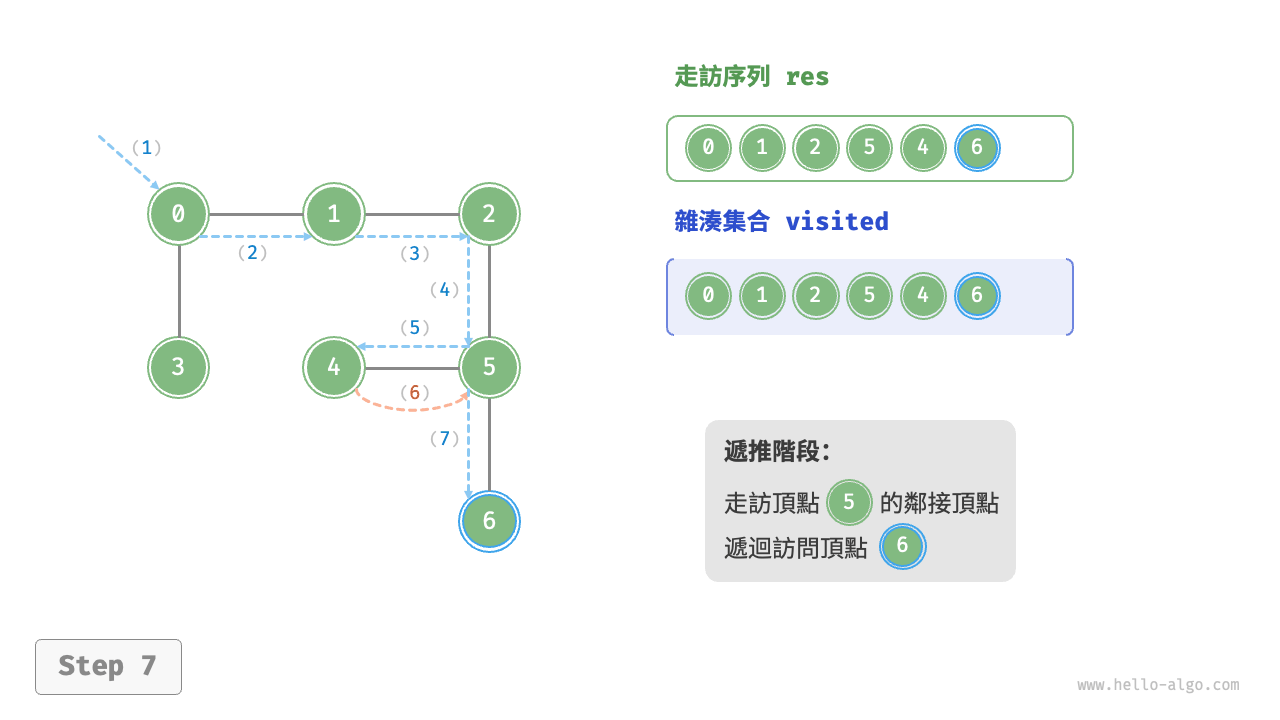
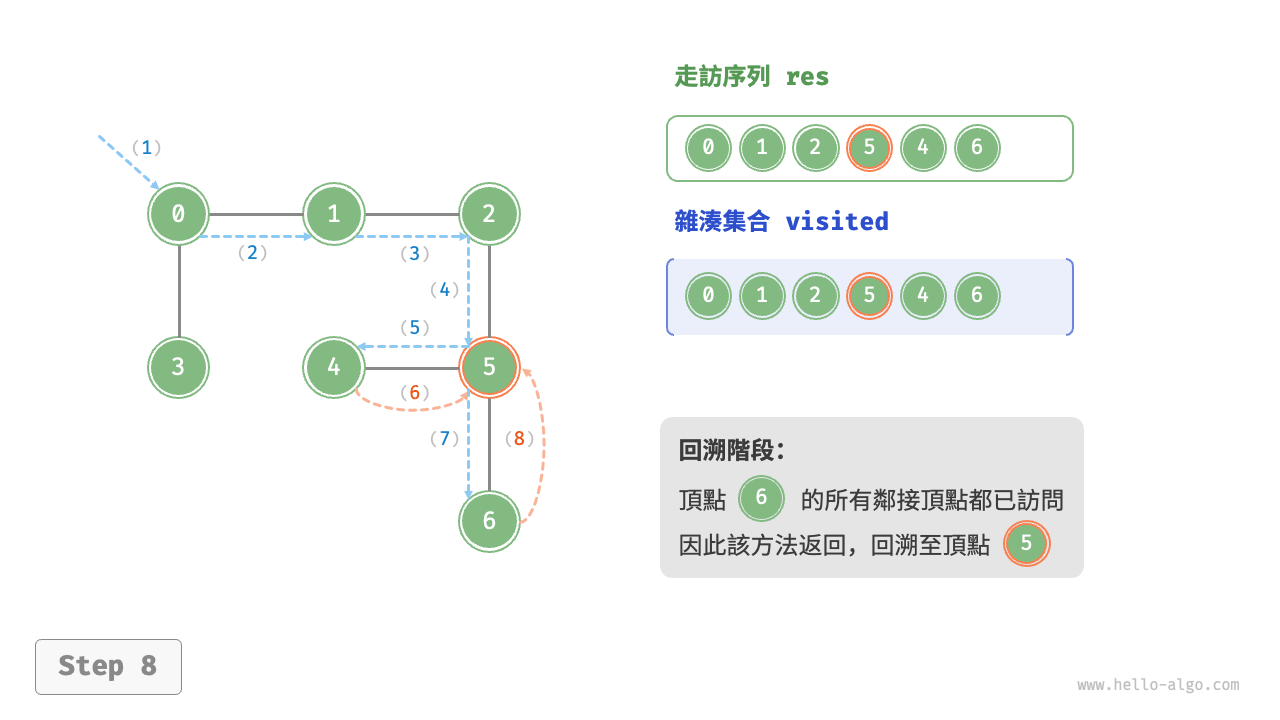
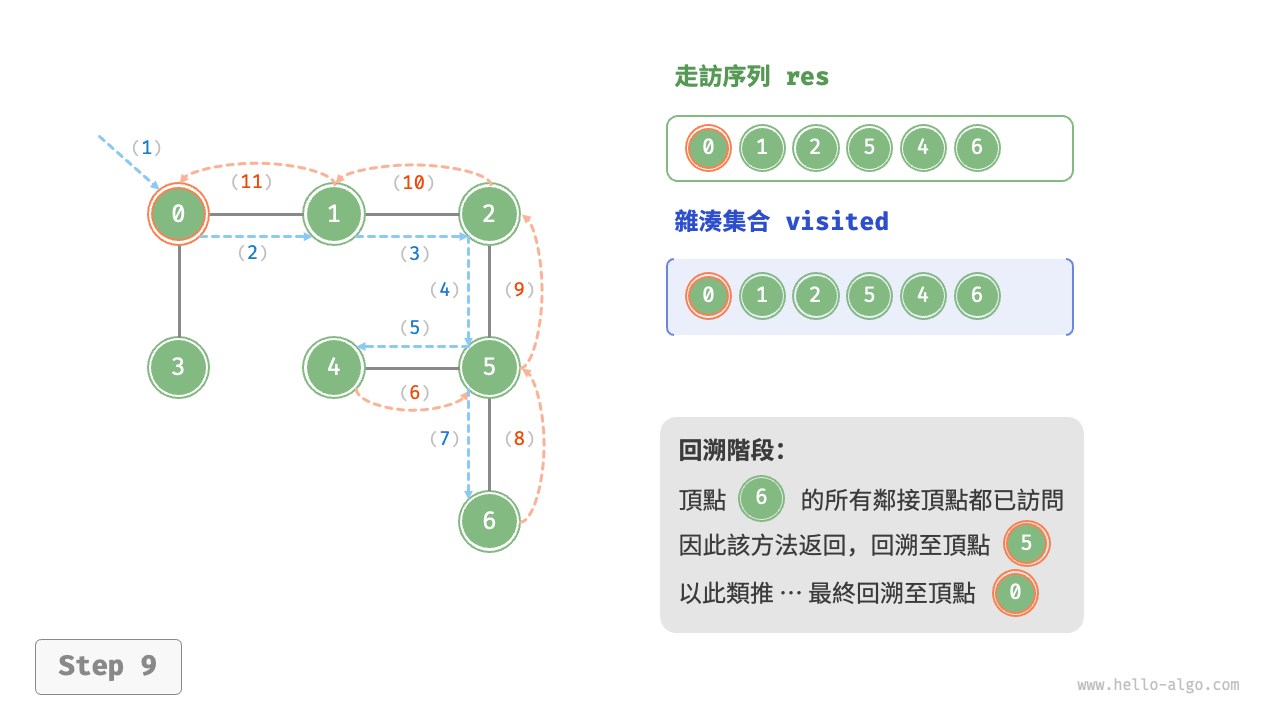
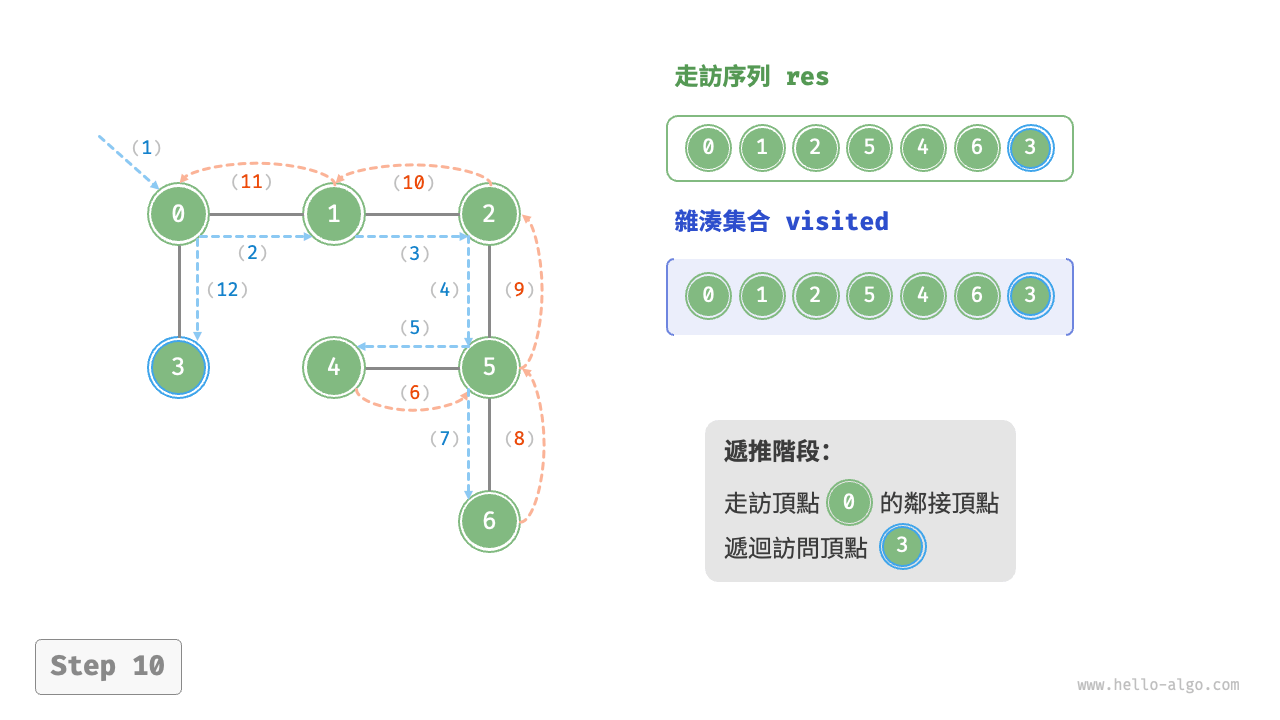
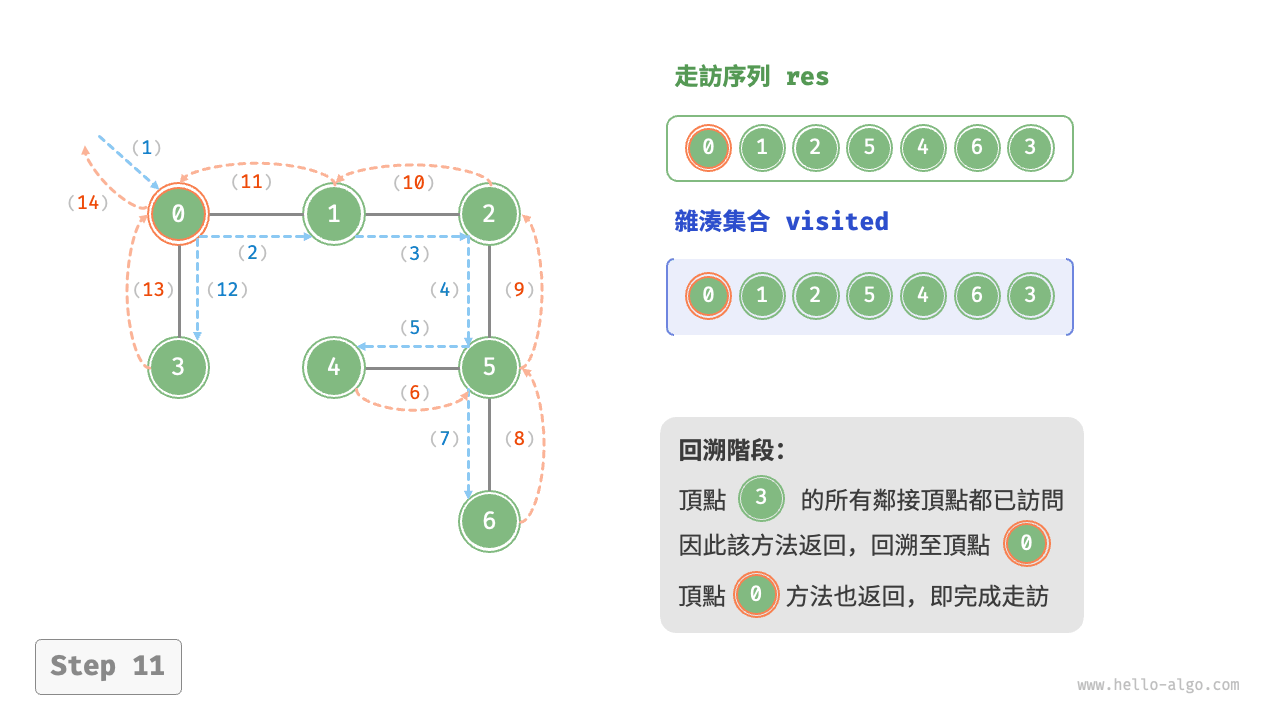
深度優先走訪的演算法流程如下圖所示。
- 直虛線代表向下遞推,表示開啟了一個新的遞迴方法來訪問新頂點。
- 曲虛線代表向上回溯,表示此遞迴方法已經返回,回溯到了開啟此方法的位置。
為了加深理解,建議將下圖與程式碼結合起來,在腦中模擬(或者用筆畫下來)整個 DFS 過程,包括每個遞迴方法何時開啟、何時返回。
!!! question "深度優先走訪的序列是否唯一?"
與廣度優先走訪類似,深度優先走訪序列的順序也不是唯一的。給定某頂點,先往哪個方向探索都可以,即鄰接頂點的順序可以任意打亂,都是深度優先走訪。
以樹的走訪為例,“根 $\rightarrow$ 左 $\rightarrow$ 右”“左 $\rightarrow$ 根 $\rightarrow$ 右”“左 $\rightarrow$ 右 $\rightarrow$ 根”分別對應前序、中序、後序走訪,它們展示了三種走訪優先順序,然而這三者都屬於深度優先走訪。
複雜度分析
時間複雜度:所有頂點都會被訪問 1 次,使用 O(|V|) 時間;所有邊都會被訪問 2 次,使用 O(2|E|) 時間;總體使用 O(|V| + |E|) 時間。
空間複雜度:串列 res ,雜湊集合 visited 頂點數量最多為 |V| ,遞迴深度最大為 |V| ,因此使用 O(|V|) 空間。