6.6 KiB
二元搜尋樹
如下圖所示,二元搜尋樹(binary search tree)滿足以下條件。
- 對於根節點,左子樹中所有節點的值
<根節點的值<右子樹中所有節點的值。 - 任意節點的左、右子樹也是二元搜尋樹,即同樣滿足條件
1.。
二元搜尋樹的操作
我們將二元搜尋樹封裝為一個類別 BinarySearchTree ,並宣告一個成員變數 root ,指向樹的根節點。
查詢節點
給定目標節點值 num ,可以根據二元搜尋樹的性質來查詢。如下圖所示,我們宣告一個節點 cur ,從二元樹的根節點 root 出發,迴圈比較節點值 cur.val 和 num 之間的大小關係。
- 若
cur.val < num,說明目標節點在cur的右子樹中,因此執行cur = cur.right。 - 若
cur.val > num,說明目標節點在cur的左子樹中,因此執行cur = cur.left。 - 若
cur.val = num,說明找到目標節點,跳出迴圈並返回該節點。
二元搜尋樹的查詢操作與二分搜尋演算法的工作原理一致,都是每輪排除一半情況。迴圈次數最多為二元樹的高度,當二元樹平衡時,使用 O(\log n) 時間。示例程式碼如下:
[file]{binary_search_tree}-[class]{binary_search_tree}-[func]{search}
插入節點
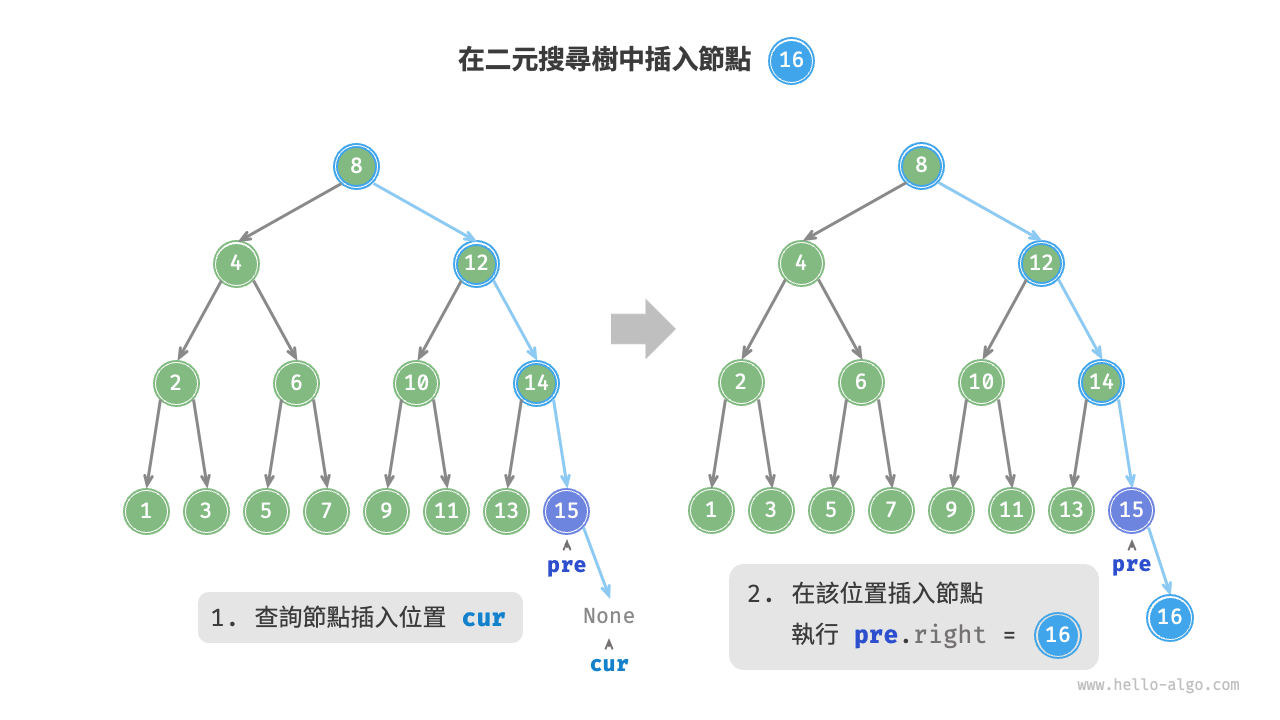
給定一個待插入元素 num ,為了保持二元搜尋樹“左子樹 < 根節點 < 右子樹”的性質,插入操作流程如下圖所示。
- 查詢插入位置:與查詢操作相似,從根節點出發,根據當前節點值和
num的大小關係迴圈向下搜尋,直到越過葉節點(走訪至None)時跳出迴圈。 - 在該位置插入節點:初始化節點
num,將該節點置於None的位置。
在程式碼實現中,需要注意以下兩點。
- 二元搜尋樹不允許存在重複節點,否則將違反其定義。因此,若待插入節點在樹中已存在,則不執行插入,直接返回。
- 為了實現插入節點,我們需要藉助節點
pre儲存上一輪迴圈的節點。這樣在走訪至None時,我們可以獲取到其父節點,從而完成節點插入操作。
[file]{binary_search_tree}-[class]{binary_search_tree}-[func]{insert}
與查詢節點相同,插入節點使用 O(\log n) 時間。
刪除節點
先在二元樹中查詢到目標節點,再將其刪除。與插入節點類似,我們需要保證在刪除操作完成後,二元搜尋樹的“左子樹 < 根節點 < 右子樹”的性質仍然滿足。因此,我們根據目標節點的子節點數量,分 0、1 和 2 三種情況,執行對應的刪除節點操作。
如下圖所示,當待刪除節點的度為 0 時,表示該節點是葉節點,可以直接刪除。
如下圖所示,當待刪除節點的度為 1 時,將待刪除節點替換為其子節點即可。
當待刪除節點的度為 2 時,我們無法直接刪除它,而需要使用一個節點替換該節點。由於要保持二元搜尋樹“左子樹 < 根節點 < 右子樹”的性質,因此這個節點可以是右子樹的最小節點或左子樹的最大節點。
假設我們選擇右子樹的最小節點(中序走訪的下一個節點),則刪除操作流程如下圖所示。
- 找到待刪除節點在“中序走訪序列”中的下一個節點,記為
tmp。 - 用
tmp的值覆蓋待刪除節點的值,並在樹中遞迴刪除節點tmp。
刪除節點操作同樣使用 O(\log n) 時間,其中查詢待刪除節點需要 O(\log n) 時間,獲取中序走訪後繼節點需要 O(\log n) 時間。示例程式碼如下:
[file]{binary_search_tree}-[class]{binary_search_tree}-[func]{remove}
中序走訪有序
如下圖所示,二元樹的中序走訪遵循“左 \rightarrow 根 \rightarrow 右”的走訪順序,而二元搜尋樹滿足“左子節點 < 根節點 < 右子節點”的大小關係。
這意味著在二元搜尋樹中進行中序走訪時,總是會優先走訪下一個最小節點,從而得出一個重要性質:二元搜尋樹的中序走訪序列是升序的。
利用中序走訪升序的性質,我們在二元搜尋樹中獲取有序資料僅需 O(n) 時間,無須進行額外的排序操作,非常高效。
二元搜尋樹的效率
給定一組資料,我們考慮使用陣列或二元搜尋樹儲存。觀察下表,二元搜尋樹的各項操作的時間複雜度都是對數階,具有穩定且高效的效能。只有在高頻新增、低頻查詢刪除資料的場景下,陣列比二元搜尋樹的效率更高。
表 陣列與搜尋樹的效率對比
| 無序陣列 | 二元搜尋樹 | |
|---|---|---|
| 查詢元素 | O(n) |
O(\log n) |
| 插入元素 | O(1) |
O(\log n) |
| 刪除元素 | O(n) |
O(\log n) |
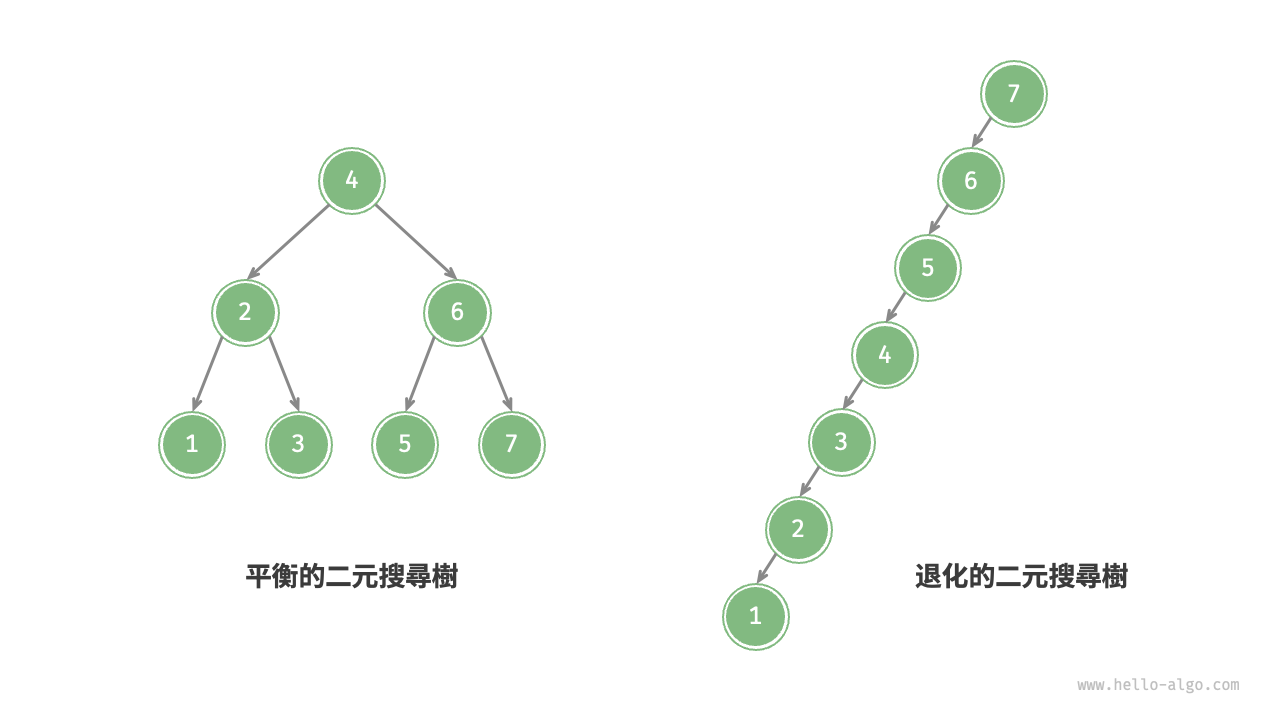
在理想情況下,二元搜尋樹是“平衡”的,這樣就可以在 \log n 輪迴圈內查詢任意節點。
然而,如果我們在二元搜尋樹中不斷地插入和刪除節點,可能導致二元樹退化為下圖所示的鏈結串列,這時各種操作的時間複雜度也會退化為 O(n) 。
二元搜尋樹常見應用
- 用作系統中的多級索引,實現高效的查詢、插入、刪除操作。
- 作為某些搜尋演算法的底層資料結構。
- 用於儲存資料流,以保持其有序狀態。