hello-algo/docs/chapter_tree/binary_search_tree.md

二叉搜索树

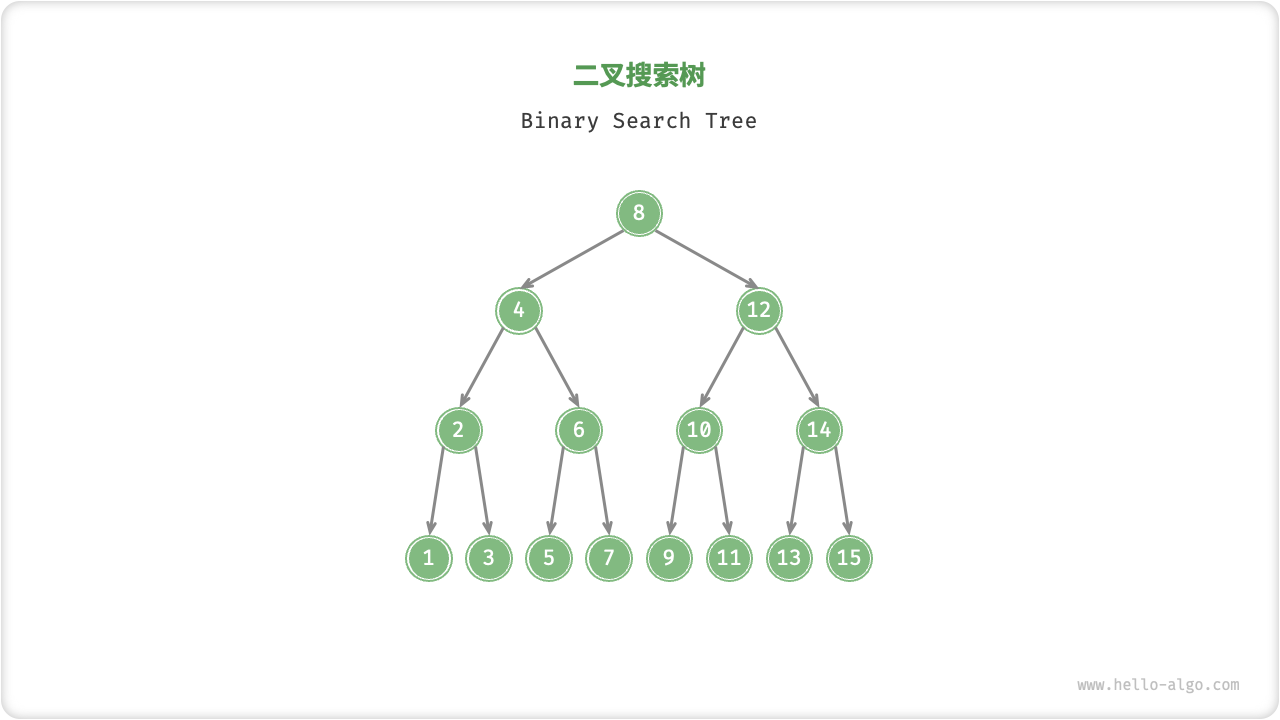
「二叉搜索树 binary search tree」满足以下条件：

1. 对于根节点，左子树中所有节点的值 < 根节点的值 < 右子树中所有节点的值。
2. 任意节点的左、右子树也是二叉搜索树，即同样满足条件 1. 。

二叉搜索树的操作

我们将二叉搜索树封装为一个类 ArrayBinaryTree ，并声明一个成员变量 root ，指向树的根节点。

查找节点

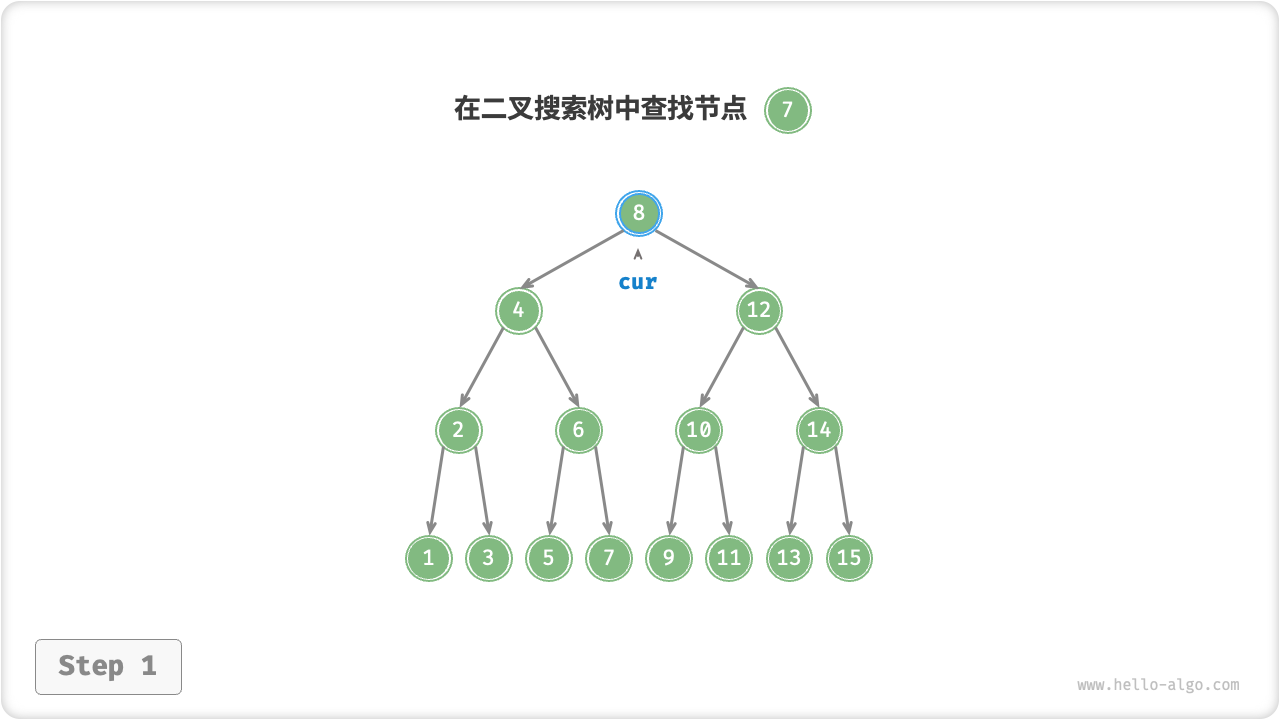
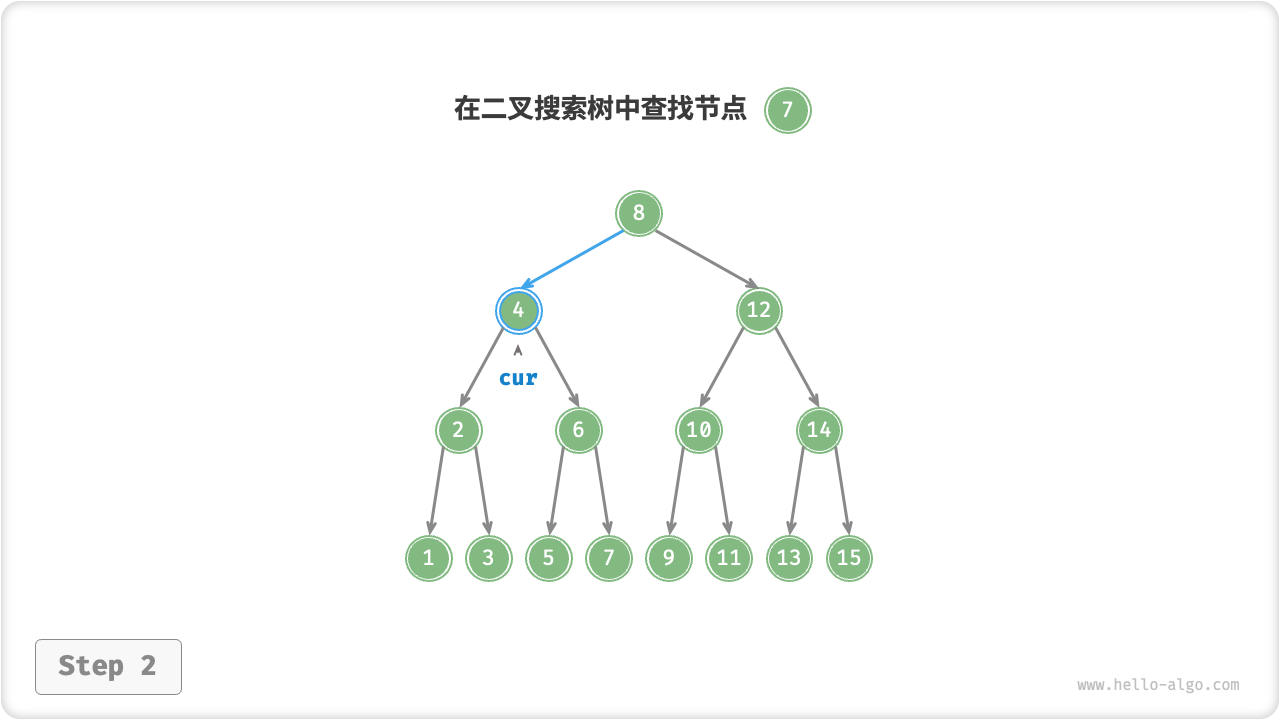
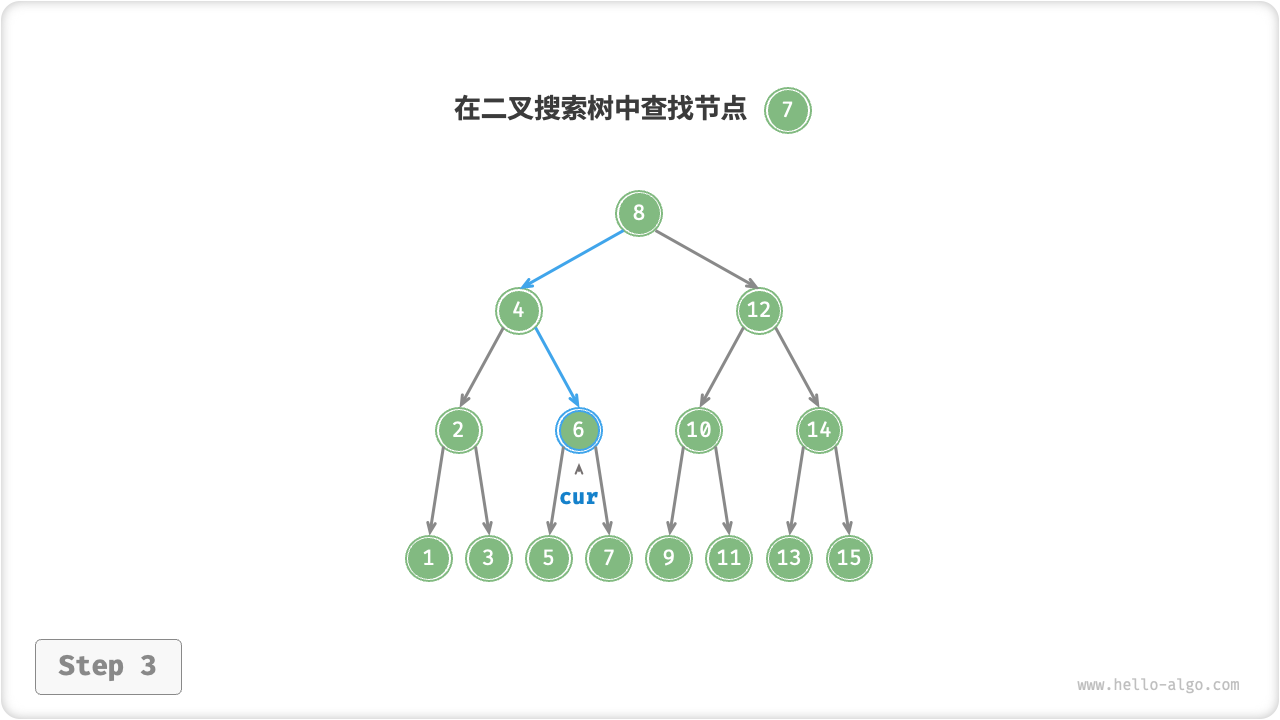
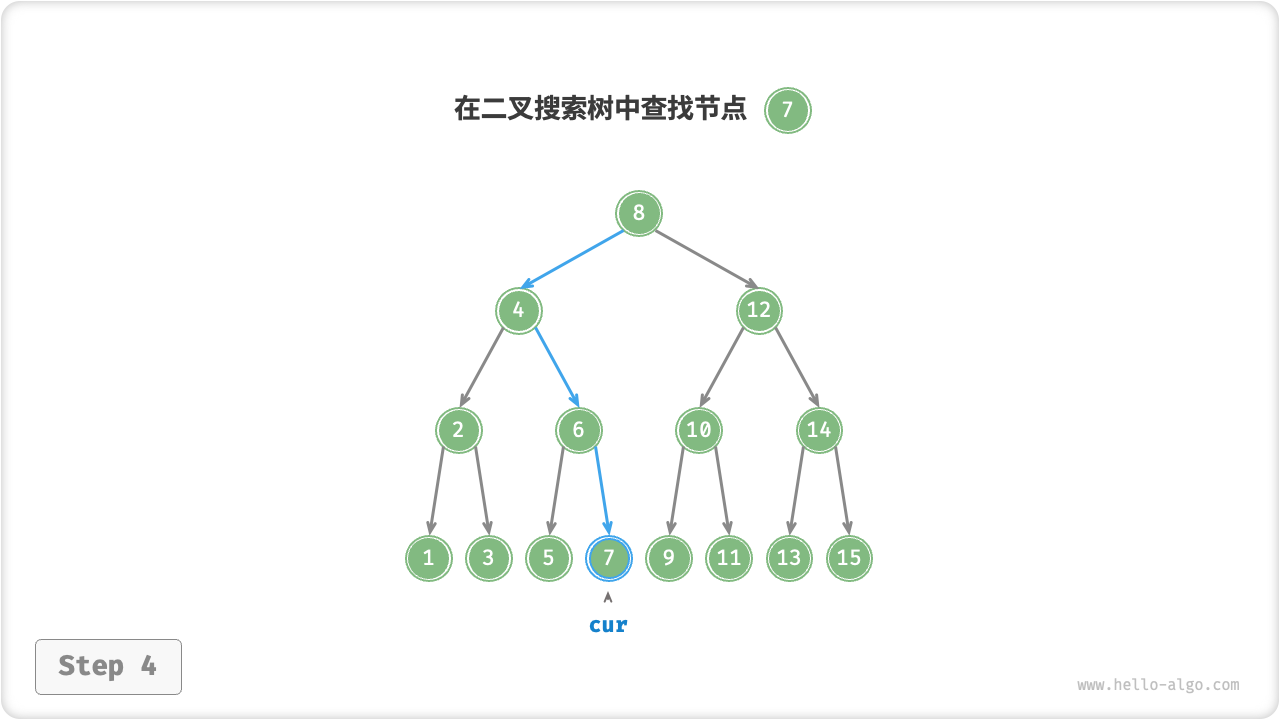
给定目标节点值 num ，可以根据二叉搜索树的性质来查找。我们声明一个节点 cur ，从二叉树的根节点 root 出发，循环比较节点值 cur.val 和 num 之间的大小关系

• 若 cur.val < num ，说明目标节点在 cur 的右子树中，因此执行 cur = cur.right 。
• 若 cur.val > num ，说明目标节点在 cur 的左子树中，因此执行 cur = cur.left 。
• 若 cur.val = num ，说明找到目标节点，跳出循环并返回该节点。

=== "<1>"

=== "<2>"

=== "<3>"

=== "<4>"

二叉搜索树的查找操作与二分查找算法的工作原理一致，都是每轮排除一半情况。循环次数最多为二叉树的高度，当二叉树平衡时，使用 O(\log n) 时间。

=== "Java"

```java title="binary_search_tree.java"
[class]{BinarySearchTree}-[func]{search}
```

=== "C++"

```cpp title="binary_search_tree.cpp"
[class]{BinarySearchTree}-[func]{search}
```

=== "Python"

```python title="binary_search_tree.py"
[class]{BinarySearchTree}-[func]{search}
```

=== "Go"

```go title="binary_search_tree.go"
[class]{binarySearchTree}-[func]{search}
```

=== "JS"

```javascript title="binary_search_tree.js"
[class]{}-[func]{search}
```

=== "TS"

```typescript title="binary_search_tree.ts"
[class]{}-[func]{search}
```

=== "C"

```c title="binary_search_tree.c"
[class]{binarySearchTree}-[func]{search}
```

=== "C#"

```csharp title="binary_search_tree.cs"
[class]{BinarySearchTree}-[func]{search}
```

=== "Swift"

```swift title="binary_search_tree.swift"
[class]{BinarySearchTree}-[func]{search}
```

=== "Zig"

```zig title="binary_search_tree.zig"
[class]{BinarySearchTree}-[func]{search}
```

=== "Dart"

```dart title="binary_search_tree.dart"
[class]{BinarySearchTree}-[func]{search}
```

=== "Rust"

```rust title="binary_search_tree.rs"
[class]{BinarySearchTree}-[func]{search}
```

插入节点

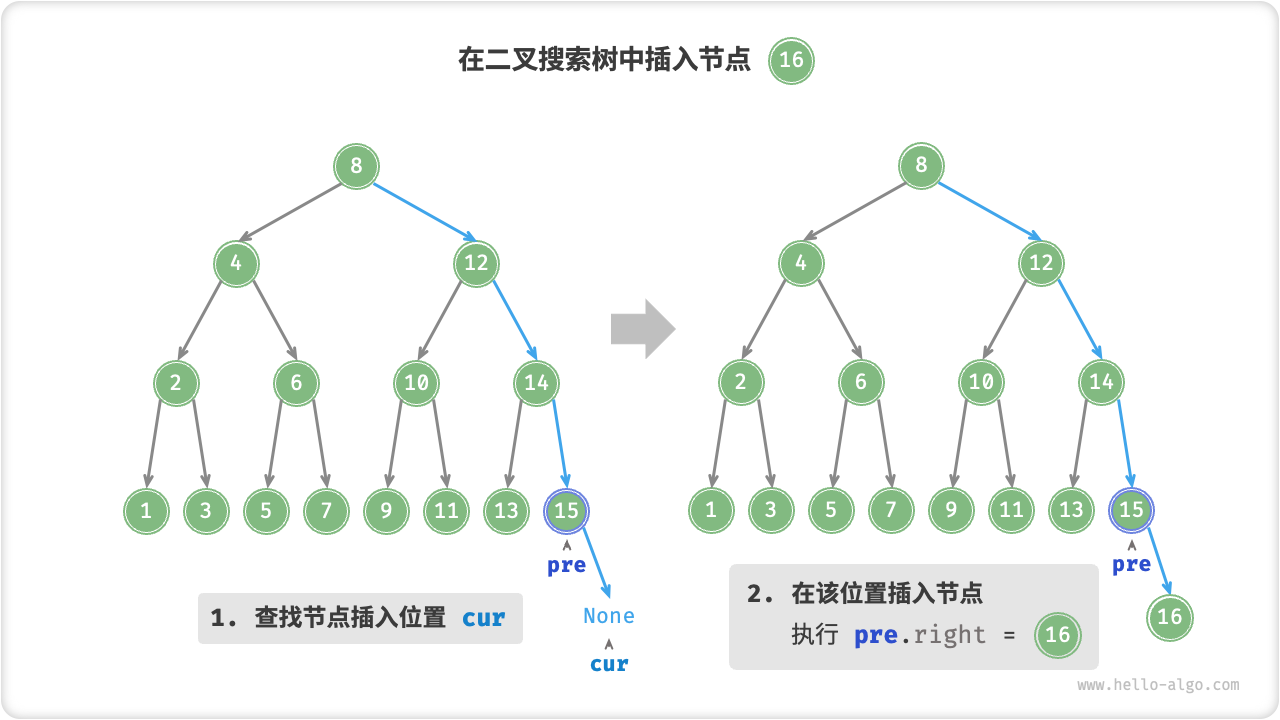
给定一个待插入元素 num ，为了保持二叉搜索树“左子树 < 根节点 < 右子树”的性质，插入操作分为两步：

1. 查找插入位置：与查找操作相似，从根节点出发，根据当前节点值和 num 的大小关系循环向下搜索，直到越过叶节点（遍历至 \text{None} ）时跳出循环。
2. 在该位置插入节点：初始化节点 num ，将该节点置于 \text{None} 的位置。

二叉搜索树不允许存在重复节点，否则将违反其定义。因此，若待插入节点在树中已存在，则不执行插入，直接返回。

=== "Java"

```java title="binary_search_tree.java"
[class]{BinarySearchTree}-[func]{insert}
```

=== "C++"

```cpp title="binary_search_tree.cpp"
[class]{BinarySearchTree}-[func]{insert}
```

=== "Python"

```python title="binary_search_tree.py"
[class]{BinarySearchTree}-[func]{insert}
```

=== "Go"

```go title="binary_search_tree.go"
[class]{binarySearchTree}-[func]{insert}
```

=== "JS"

```javascript title="binary_search_tree.js"
[class]{}-[func]{insert}
```

=== "TS"

```typescript title="binary_search_tree.ts"
[class]{}-[func]{insert}
```

=== "C"

```c title="binary_search_tree.c"
[class]{binarySearchTree}-[func]{insert}
```

=== "C#"

```csharp title="binary_search_tree.cs"
[class]{BinarySearchTree}-[func]{insert}
```

=== "Swift"

```swift title="binary_search_tree.swift"
[class]{BinarySearchTree}-[func]{insert}
```

=== "Zig"

```zig title="binary_search_tree.zig"
[class]{BinarySearchTree}-[func]{insert}
```

=== "Dart"

```dart title="binary_search_tree.dart"
[class]{BinarySearchTree}-[func]{insert}
```

=== "Rust"

```rust title="binary_search_tree.rs"
[class]{BinarySearchTree}-[func]{insert}
```

为了插入节点，我们需要利用辅助节点 pre 保存上一轮循环的节点，这样在遍历至 \text{None} 时，我们可以获取到其父节点，从而完成节点插入操作。

与查找节点相同，插入节点使用 O(\log n) 时间。

删除节点

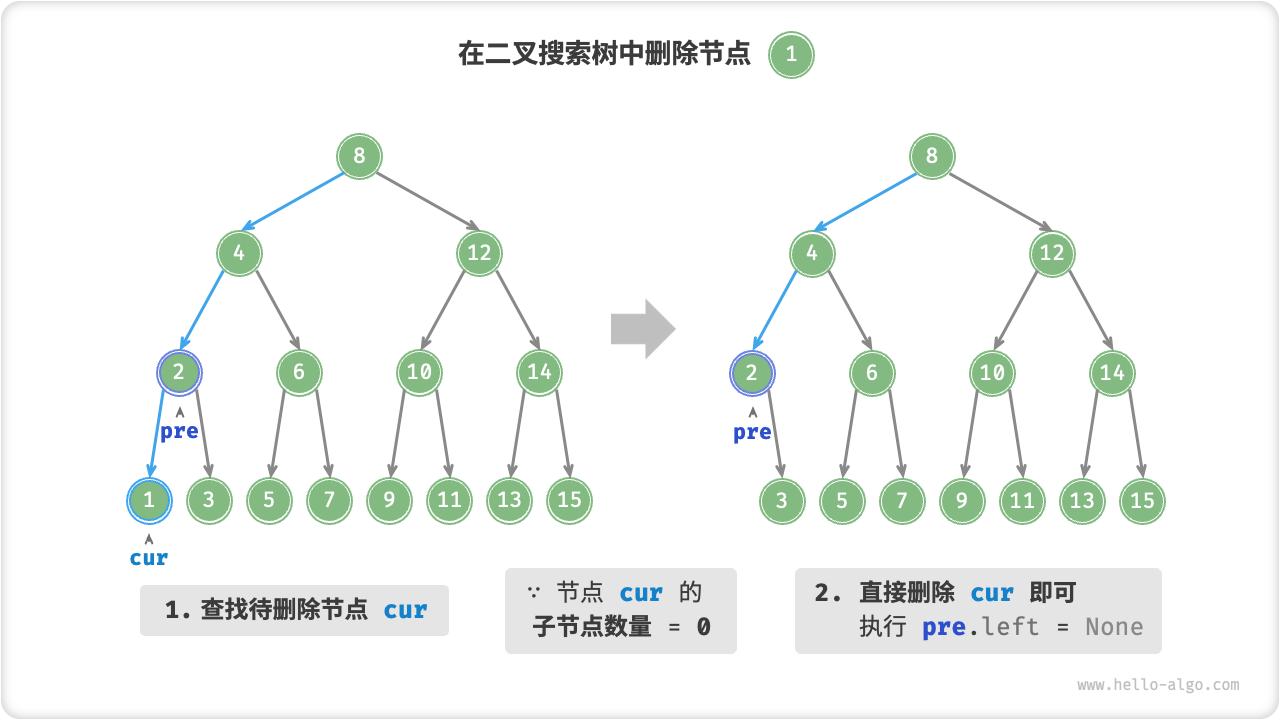
与插入节点类似，我们需要在删除操作后维持二叉搜索树的“左子树 < 根节点 < 右子树”的性质。首先，我们需要在二叉树中执行查找操作，获取待删除节点。接下来，根据待删除节点的子节点数量，删除操作需分为三种情况：

当待删除节点的度为 0 时，表示待删除节点是叶节点，可以直接删除。

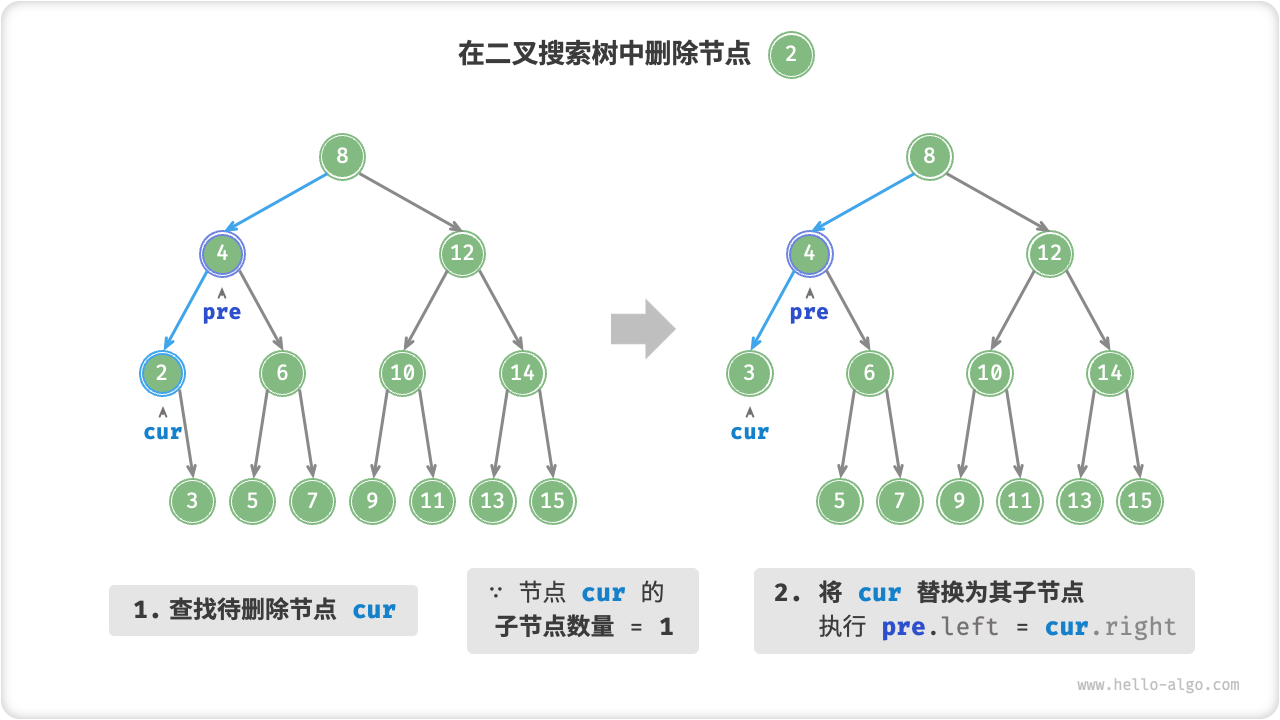
当待删除节点的度为 1 时，将待删除节点替换为其子节点即可。

当待删除节点的度为 2 时，我们无法直接删除它，而需要使用一个节点替换该节点。由于要保持二叉搜索树“左 < 根 < 右”的性质，因此这个节点可以是右子树的最小节点或左子树的最大节点。

假设我们选择右子树的最小节点（即中序遍历的下一个节点），则删除操作为：

1. 找到待删除节点在“中序遍历序列”中的下一个节点，记为 tmp 。
2. 将 tmp 的值覆盖待删除节点的值，并在树中递归删除节点 tmp 。

=== "<1>"

=== "<2>"

=== "<3>"

=== "<4>"

删除节点操作同样使用 O(\log n) 时间，其中查找待删除节点需要 O(\log n) 时间，获取中序遍历后继节点需要 O(\log n) 时间。

=== "Java"

```java title="binary_search_tree.java"
[class]{BinarySearchTree}-[func]{remove}
```

=== "C++"

```cpp title="binary_search_tree.cpp"
[class]{BinarySearchTree}-[func]{remove}
```

=== "Python"

```python title="binary_search_tree.py"
[class]{BinarySearchTree}-[func]{remove}
```

=== "Go"

```go title="binary_search_tree.go"
[class]{binarySearchTree}-[func]{remove}
```

=== "JS"

```javascript title="binary_search_tree.js"
[class]{}-[func]{remove}
```

=== "TS"

```typescript title="binary_search_tree.ts"
[class]{}-[func]{remove}
```

=== "C"

```c title="binary_search_tree.c"
[class]{binarySearchTree}-[func]{removeNode}
```

=== "C#"

```csharp title="binary_search_tree.cs"
[class]{BinarySearchTree}-[func]{remove}
```

=== "Swift"

```swift title="binary_search_tree.swift"
[class]{BinarySearchTree}-[func]{remove}
```

=== "Zig"

```zig title="binary_search_tree.zig"
[class]{BinarySearchTree}-[func]{remove}
```

=== "Dart"

```dart title="binary_search_tree.dart"
[class]{BinarySearchTree}-[func]{remove}
```

=== "Rust"

```rust title="binary_search_tree.rs"
[class]{BinarySearchTree}-[func]{remove}
```

排序

我们知道，二叉树的中序遍历遵循“左 \rightarrow 根 \rightarrow 右”的遍历顺序，而二叉搜索树满足“左子节点 < 根节点 < 右子节点”的大小关系。因此，在二叉搜索树中进行中序遍历时，总是会优先遍历下一个最小节点，从而得出一个重要性质：二叉搜索树的中序遍历序列是升序的。

利用中序遍历升序的性质，我们在二叉搜索树中获取有序数据仅需 O(n) 时间，无须额外排序，非常高效。

二叉搜索树的效率

给定一组数据，我们考虑使用数组或二叉搜索树存储。

观察可知，二叉搜索树的各项操作的时间复杂度都是对数阶，具有稳定且高效的性能表现。只有在高频添加、低频查找删除的数据适用场景下，数组比二叉搜索树的效率更高。

表：数组与搜索树的效率对比

	无序数组	二叉搜索树
查找元素	O(n)	O(\log n)
插入元素	O(1)	O(\log n)
删除元素	O(n)	O(\log n)

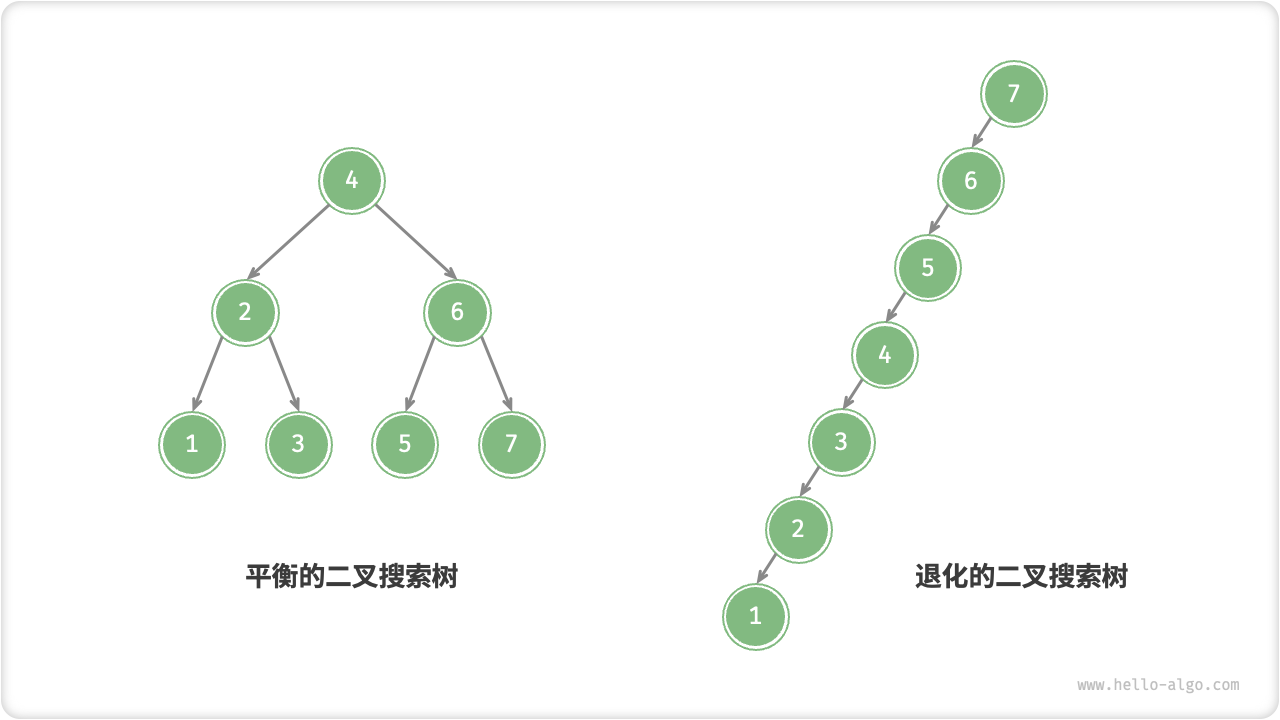
在理想情况下，二叉搜索树是“平衡”的，这样就可以在 \log n 轮循环内查找任意节点。

然而，如果我们在二叉搜索树中不断地插入和删除节点，可能导致二叉树退化为链表，这时各种操作的时间复杂度也会退化为 O(n) 。

二叉搜索树常见应用

• 用作系统中的多级索引，实现高效的查找、插入、删除操作。
• 作为某些搜索算法的底层数据结构。
• 用于存储数据流，以保持其有序状态。