5.5 KiB
哈希冲突
在理想情况下,哈希函数应为每个输入生成唯一的输出,实现 key 和 value 的一一对应。然而实际上,向哈希函数输入不同的 key 却产生相同输出的情况是存在的,这种现象被称为「哈希冲突 Hash Collision」。哈希冲突可能导致查询结果错误,从而严重影响哈希表的可用性。
那么,为何会出现哈希冲突呢?从本质上看,由于哈希函数的输入空间通常远大于输出空间,因此多个输入产生相同输出的情况是不可避免的。例如,若输入空间为全体整数,而输出空间为固定大小的数组,则必然有多个整数映射至同一数组索引。
为了减轻哈希冲突,一方面,可以通过扩大哈希表容量来降低冲突概率。极端情况下,当输入空间和输出空间大小相等时,哈希表等同于数组,每个 key 都对应唯一的数组索引,可谓“大力出奇迹”。
另一方面,可以考虑优化哈希表的表示以缓解哈希冲突,常用方法包括「链式地址 Separate Chaining」和「开放寻址 Open Addressing」。
哈希表扩容
哈希函数的最后一步通常是对桶数量 n 取余,作用是将哈希值映射到桶索引范围,从而将 key 放入对应的桶中。当哈希表容量越大(即 n 越大)时,多个 key 被分配到同一个桶中的概率就越低,冲突就越少。
因此,当哈希表内的冲突总体较为严重时,编程语言通常通过扩容哈希表来缓解冲突。类似于数组扩容,哈希表扩容需将所有键值对从原哈希表迁移至新哈希表,开销较大。
编程语言通常使用「负载因子 Load Factor」来衡量哈希冲突的严重程度,定义为哈希表中元素数量除以桶数量,常作为哈希表扩容的触发条件。在 Java 中,当负载因子 > 0.75 时,系统会将 HashMap 容量扩展为原先的 2 倍。
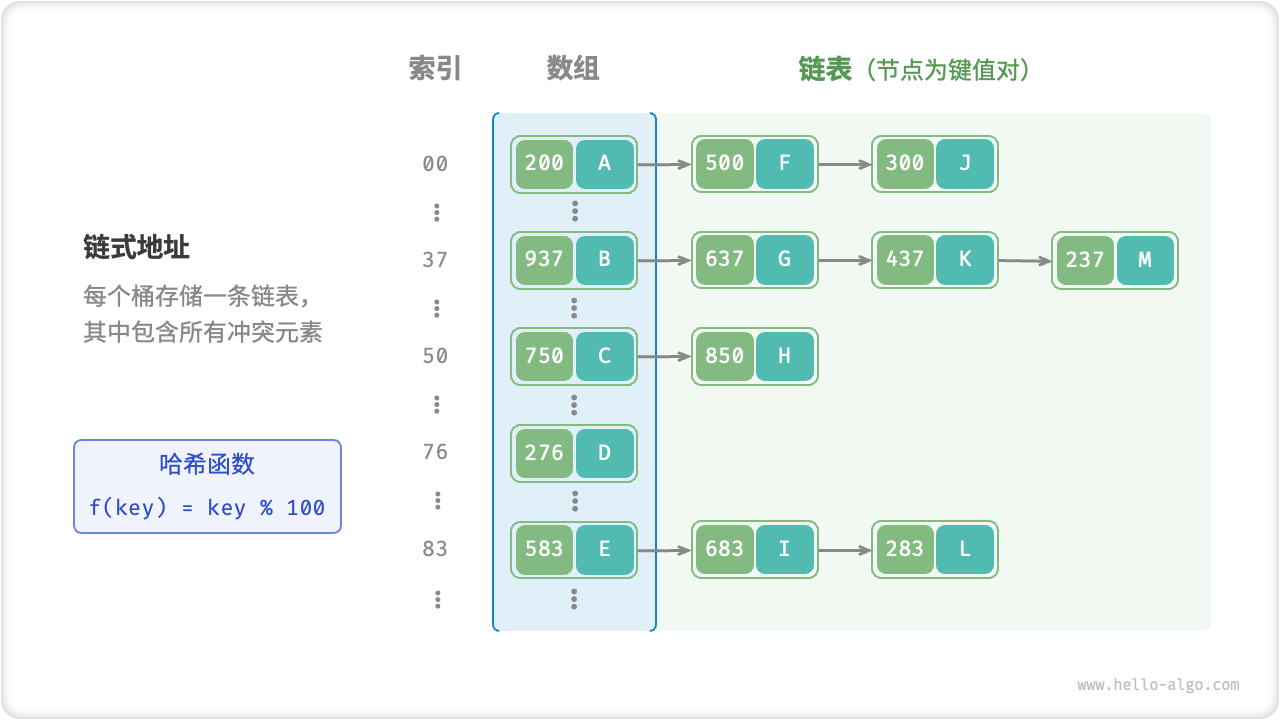
链式地址
在原始哈希表中,每个桶仅能存储一个键值对。链式地址将单个元素转换为链表,将键值对作为链表节点,将所有发生冲突的键值对都存储在同一链表中。
链式地址下,哈希表的操作方法包括:
- 查询元素:输入 key ,经过哈希函数得到数组索引,即可访问链表头节点,然后遍历链表并对比 key 以查找目标键值对。
- 添加元素:先通过哈希函数访问链表头节点,然后将节点(即键值对)添加到链表中。
- 删除元素:根据哈希函数的结果访问链表头部,接着遍历链表以查找目标节点,并将其删除。
尽管链式地址法解决了哈希冲突问题,但仍存在一些局限性,包括:
- 占用空间增大,由于链表或二叉树包含节点指针,相比数组更加耗费内存空间;
- 查询效率降低,因为需要线性遍历链表来查找对应元素;
为了提高操作效率,可以将链表转换为「AVL 树」或「红黑树」,将查询操作的时间复杂度优化至 O(\log n) 。
开放寻址
「开放寻址」方法不引入额外的数据结构,而是通过“多次探测”来解决哈希冲突,探测方式主要包括线性探测、平方探测、多次哈希。
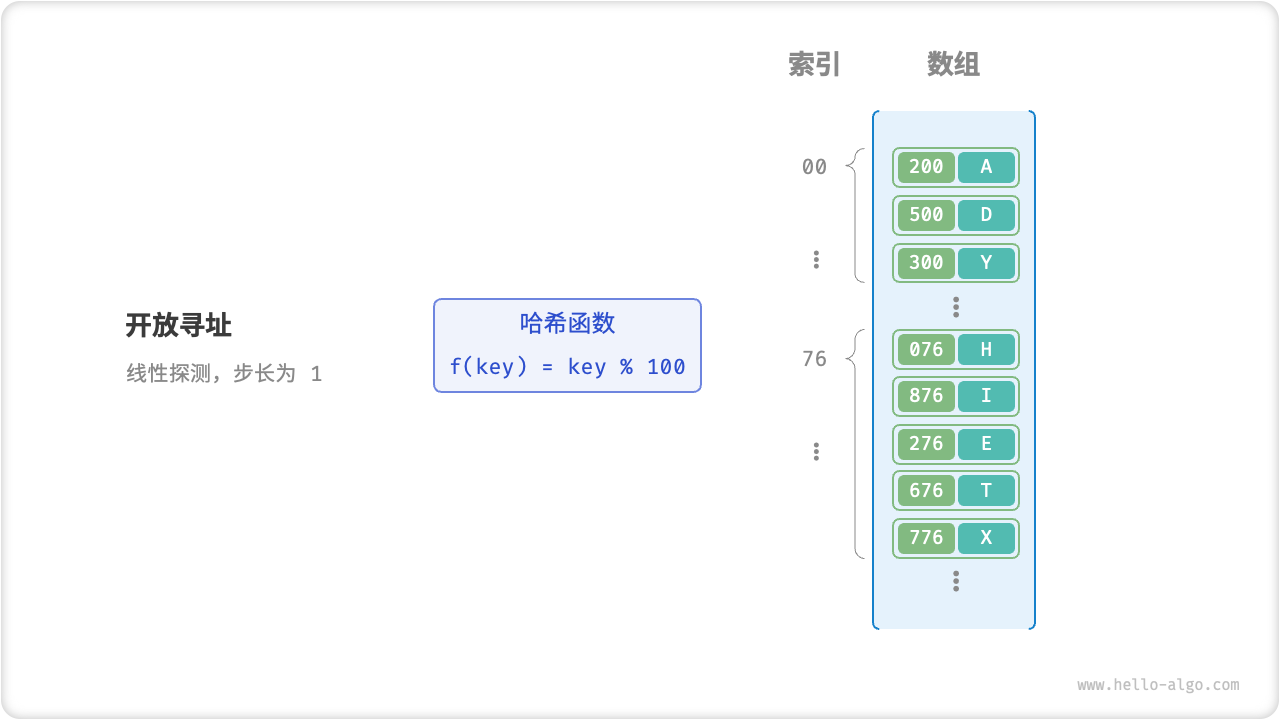
线性探测
「线性探测」采用固定步长的线性查找来解决哈希冲突。
插入元素:若出现哈希冲突,则从冲突位置向后线性遍历(步长通常为 1 ),直至找到空位,将元素插入其中。
查找元素:在出现哈希冲突时,使用相同步长进行线性查找,可能遇到以下两种情况。
- 找到对应元素,返回 value 即可;
- 若遇到空位,说明目标键值对不在哈希表中;
线性探测存在以下缺陷:
- 不能直接删除元素。删除元素会在数组内产生一个空位,查找其他元素时,该空位可能导致程序误判元素不存在(即上述第
2.种情况)。因此,需要借助一个标志位来标记已删除元素。 - 容易产生聚集。数组内连续被占用位置越长,这些连续位置发生哈希冲突的可能性越大,进一步促使这一位置的“聚堆生长”,最终导致增删查改操作效率降低。
多次哈希
顾名思义,「多次哈希」方法是使用多个哈希函数 f_1(x) , f_2(x) , f_3(x) , \cdots 进行探测。
插入元素:若哈希函数 f_1(x) 出现冲突,则尝试 f_2(x) ,以此类推,直到找到空位后插入元素。
查找元素:在相同的哈希函数顺序下进行查找,存在以下两种情况:
- 如果找到目标元素,则返回之;
- 若遇到空位或已尝试所有哈希函数,则说明哈希表中不存在该元素;
与线性探测相比,多次哈希方法不易产生聚集,但多个哈希函数会增加额外的计算量。
!!! note "哈希表设计方案"
Java 采用「链式地址」。自 JDK 1.8 以来,当 HashMap 内数组长度达到 64 且链表长度达到 8 时,链表会被转换为红黑树以提升查找性能。
Python 采用「开放寻址」。字典 dict 使用伪随机数进行探测。
Golang 采用「链式地址」。Go 规定每个桶最多存储 8 个键值对,超出容量则连接一个溢出桶;当溢出桶过多时,会执行一次特殊的等量扩容操作,以确保性能。