hello-algo/en/docs/chapter_heap/top_k.md

Top-k problem

!!! question

Given an unordered array `nums` of length $n$, return the largest $k$ elements in the array.

For this problem, we will first introduce two straightforward solutions, then explain a more efficient heap-based method.

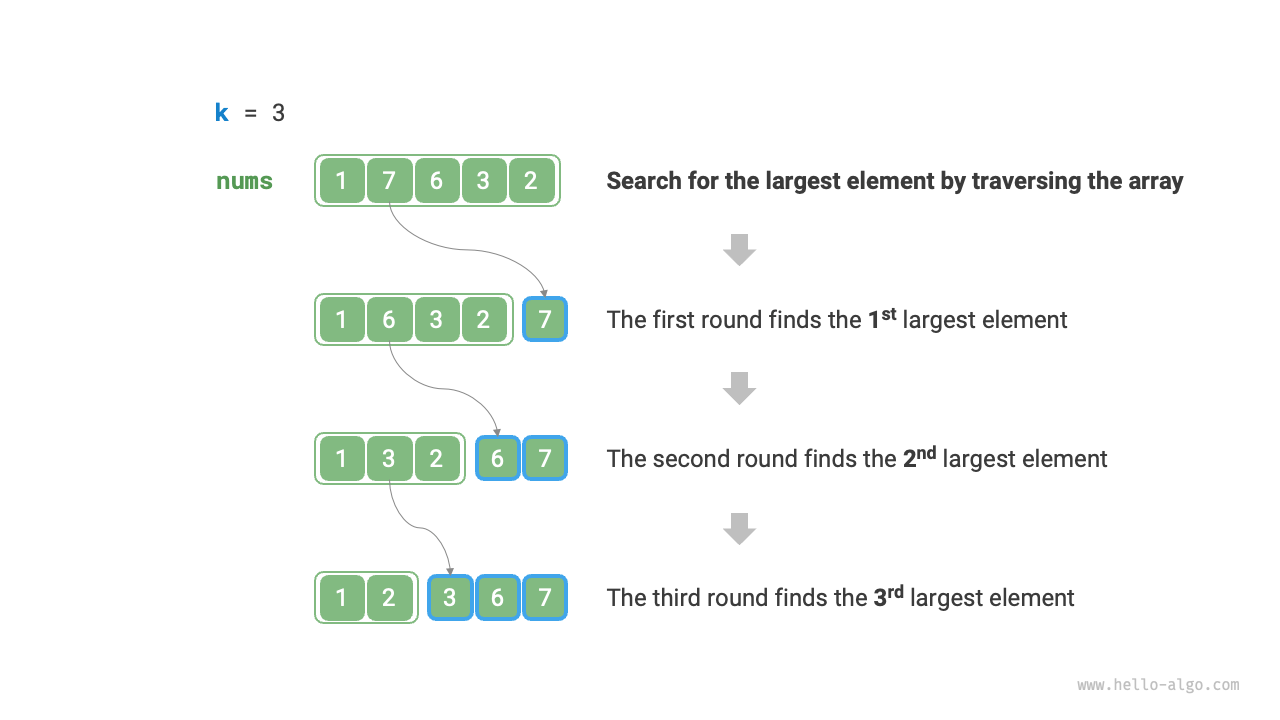
Method 1: Iterative selection

We can perform k rounds of iterations as shown in the figure below, extracting the 1^{st}, 2^{nd}, \dots, k^{th} largest elements in each round, with a time complexity of O(nk).

This method is only suitable when k \ll n, as the time complexity approaches O(n^2) when k is close to n, which is very time-consuming.

!!! tip

When $k = n$, we can obtain a complete ordered sequence, which is equivalent to the "selection sort" algorithm.

Method 2: Sorting

As shown in the figure below, we can first sort the array nums and then return the last k elements, with a time complexity of O(n \log n).

Clearly, this method "overachieves" the task, as we only need to find the largest k elements, without the need to sort the other elements.

Method 3: Heap

We can solve the Top-k problem more efficiently based on heaps, as shown in the following process.

1. Initialize a min heap, where the top element is the smallest.
2. First, insert the first k elements of the array into the heap.
3. Starting from the k + 1^{th} element, if the current element is greater than the top element of the heap, remove the top element of the heap and insert the current element into the heap.
4. After completing the traversal, the heap contains the largest k elements.

=== "<1>"

=== "<2>"

=== "<3>"

=== "<4>"

=== "<5>"

=== "<6>"

=== "<7>"

=== "<8>"

=== "<9>"

Example code is as follows:

[file]{top_k}-[class]{}-[func]{top_k_heap}

A total of n rounds of heap insertions and deletions are performed, with the maximum heap size being k, hence the time complexity is O(n \log k). This method is very efficient; when k is small, the time complexity tends towards O(n); when k is large, the time complexity will not exceed O(n \log n).

Additionally, this method is suitable for scenarios with dynamic data streams. By continuously adding data, we can maintain the elements within the heap, thereby achieving dynamic updates of the largest k elements.